Zbierka úloh (MO kat. C a vybrané úlohy kat. B)
Zvolte kategorii úloh:
- Krajské kolo
- Školské kolo
- Návodná úloha
- Úloha domáceho kola
- Doplňujúca úloha
Úloha 64-I-5-N5
Riešenie
Tvrdenie pre najmenší spoločný násobok neplatí, uvedieme protipríklad. Pre čísla \(a=12\), \(b=8\), \(a+b=20\), \(a-b=4\), \([12,8]=24\), avšak \([12,8,20,4]=120\).
Komentár
Úloha precvičuje dôkaz všeobecného tvrdenia a opäť prináša protipríklad ako dostatočný argument.Úloha 59-I-1-N1
Riešenie*
Úloha 63-I-6-N3
Riešenie*
Úloha 63-I-2-N2
\(A\), \(C\), \(V\),
\(A\), \(U\), \(R\),
\(A\), \(P\), \(Q\),
\(A\), \(B\), \(R\).
Riešenie*
Úloha 61-I-1-N5
Riešenie*
Úloha 62-I-4-N4
Riešenie*
Úloha
Riešenie

Potom \(|\measuredangle BAC|=|\measuredangle ACX|\) a \(|\measuredangle ABC|=|\measuredangle BCY|\), pretože ide o dvojice striedavých uhlov. Keďže \(|\measuredangle ACX|+|\measuredangle ACB|+ |\measuredangle BCY|=180^\circ\), pretože uhol \(XCY\) je priamy, platí aj \(|\measuredangle BAC|+|\measuredangle ABC|+|\measuredangle ACB|=180^\circ\).
Úloha 64-I-6-N1
Riešenie*
Úloha 62-I-5-N2
Riešenie*
Úloha 65-I-4-N3
Riešenie*
Úloha 57-I-4-D4
Riešenie*
Úloha 59-I-4-D1
Riešenie*
Úloha 61-I-4-N3
Riešenie*
Úloha B-66-I-5
Riešenie*
Ak označíme zvyčajným spôsobom uhly pri vrcholoch \(A\) a \(B\) trojuholníka \(ABC\), je zároveň \(|\measuredangle ACD| = 90^\circ-\alpha = \beta\) a \(|\measuredangle BCD| = 90^ \circ -\beta = \alpha\) . Z toho vyplýva podobnosť trojuholníkov \(CDM \sim BDN\) a \(ADM \sim CDN\), takže \[\frac{|MD|}{|ND|}=\frac{|CM|}{|BN|} \ \ \ \ \mathrm{a} \ \ \ \ \frac{|MD|}{|ND|}=\frac{|AM|}{|CN|}.\] Porovnaním pravých strán dostaneme \[\label{eq:B66I5}
|AM| \cdot |BN| = |CM| \cdot |CN|.\]
Keďže obvodové uhly nad tetivami \(CM\) a \(CN\) sú zhodné, je \(|CM| = |CN|\). Použitím Pytagorovej vety v pravouhlom (rovnoramennom) trojuholníku \(CMN\) tak dostaneme \[2|CM|^2= |CM|^2+ |CN|^2= |MN|^2\] a dosadením do rovnosti [eq:B66I5] vyjde \[2|AM| \cdot |BN| = 2|CM| \cdot |CN| = 2 \cdot |CM|^2= |MN|^2.\] Tým je tvrdenie úlohy dokázané.
Poznámka. Ukážeme ešte jeden spôsob odvodenia kľúčovej rovnosti [eq:B66I5]. Pravouhlé trojuholníky \(ACD\) a \(CBD\) sú podobné, pretože \(|\measuredangle BCD| = 90^\circ- |\measuredangle ACD| = |\measuredangle CAD|\). To však znamená, že osi \(DM\) a \(DN\) oboch vnútorných uhlov z vrcholu \(D\), ktoré si v tejto podobnosti zodpovedajú, delia protiľahlé strany v rovnakom pomere. Platí teda \[|AM| : |CM| = |CN| : |BN|, \ \ \ \ \mathrm{t.\ j.} \ \ \ \ |AM| \cdot |BN| = |CM| \cdot |CN|.\]
Úloha 58-I-3-N1, resp. 56-S-1
Riešenie*
Celkom existuje 41 štvorciferných prirodzených čísel, ktoré spĺňajú podmienky.
Alternatívnym postupom je vypísanie všetkých možností na základe ciferného súčtu, ktorý musí byť deliteľný troma a zároveň sa končiť párnou cifrou.
Komentár
Úloha využíva poznatky o deliteľnosti, takže pekne nadväzuje na predchádzajúce semináre. Tiež je prvou úlohou o cifernom zápise, v riešení ktorej nevyužijeme rozvinutý zápis čísla, ale skôr intuitívne kombinatorické úvahy.Ak sa študenti vyberú cestou vypisovania všetkých možných kombinácií, skúsime ich povzbudiť, aby ich úsilie bolo čo najsystematickejšie a efektívne, príp. prediskutujeme, či sa riešenie dá nájsť aj inou cestou.
Úloha 58-I-5-N1
Riešenie*
Úloha 62-I-6-N2
Riešenie*
Úloha 59-I-3-D1
Riešenie*
Úloha B-58-I-2
Riešenie*
Prípad \(z - x = 0\). Dosadením \(z = x\) do prvej rovnice sústavy dostaneme \(x^2+ xy = y^2 + x^2\), čiže \(y(x - y) = 0\). To znamená, že platí \(y = 0\) alebo \(x = y\). V prvom prípade dostávame trojice \((x, y, z) = (x, 0, x)\), v druhom \((x, y, z) = (x, x, x)\); také trojice sú riešeniami danej sústavy pre ľubovoľné reálne číslo \(x\), ako ľahko overíme dosadením (aj keď taká skúška pri našom postupe vlastne nie je nutná). [part:a]
Prípad \(2z + 2x + y = 0\). Dosadením \(y = -2x - 2z\) do prvej rovnice sústavy dostaneme \[x^2 + x(-2x - 2z) = (-2x - 2z)^2 + z^2,\ \ \ \ \text{čiže} \ \ \ \ 5(x + z)^2 = 0.\] Posledná rovnica je splnená práve vtedy, keď \(z = -x\), vtedy však \(y = -2x - 2z = 0\).Dostávame trojice \((x, y, z) = (x, 0, -x)\), ktoré sú riešeniami danej sústavy pre každé reálne \(x\), ako overíme dosadením. (O takej skúške platí to isté čo v prípade [part:a].
Odpoveď. Všetky riešenia \((x, y, z)\) danej sústavy sú trojice troch typov: \[(x, x, x), \ \ (x, 0, x), \ \ (x, 0, -x),\] kde \(x\) je ľubovoľné reálne číslo.
Iné riešenie*. Obe rovnice sústavy sčítame. Po úprave dostaneme rovnicu \[y(x + z - 2y) = 0\] a opäť rozlíšime dve možnosti.
Prípad \(y = 0\). Z prvej rovnice sústavy ihneď vidíme, že \(x^2 = z^2\), čiže \(z =\pm x\). Skúškou overíme, že každá z trojíc \((x, 0, x)\) a \((x, 0, -x)\) je pre ľubovoľné reálne \(x\) riešením. [part:a2]
Prípad \(x + z - 2y = 0\). Dosadením \(y = \frac{1}{2}(x + z)\) do prvej rovnice sústavy dostaneme \[x^2 + x(x + z)^2=\frac{(x + z)^2}{4}+ z^2, \ \ \ \ \text{po úprave} \ \ \ \ x^2 = z^2.\] Platí teda \(z = -x\) alebo \(z = x\). Dosadením do rovnosti \(x + z - 2y = 0\) v prvom prípade dostaneme \(y = 0\), v druhom prípade \(y = x\). Zodpovedajúce trojice \((x, 0, -x)\) a \((x, x, x)\) sú riešeniami pre každé reálne \(x\) (prvé z nich sme však našli už v časti [part:a2].
Úloha 58-I-5-D1
Riešenie*
Úloha B-60-S-1
Riešenie*
Upravujme danú rovnicu: \[\begin{aligned} \sqrt{3} +\sqrt{x + 3} & = p, \nonumber\\ 2x + 3 + 2\sqrt{x(x + 3)} & = p^2,\nonumber \\ 2\sqrt{x(x + 3)} & = p^2- 2x - 3,\nonumber \\ 4x(x + 3) & = (p^2 -2x - 3)^2,\nonumber \\ 4x^2+ 12x & = p^4+ 4x^2+ 9 - 4p^2x - 6p^2+ 12x, \nonumber\\ x & = \frac{(p^2 - 3)^2}{4p^2}. \label{eq:B60S1}\end{aligned}\] Keďže sme danú rovnicu umocňovali na druhú, je nutné sa presvedčiť skúškou, že vypočítané \(x\) je pre hodnotu parametra \(p \geq \sqrt{3}\) riešením pôvodnej rovnice: \[\begin{aligned} \sqrt{\frac{(p^2 - 3)^2}{4p^2}+ 3} +\sqrt{\frac{(p^2 - 3)^2}{4p^2}} & = \sqrt{\frac{p^4 - 6p^2 + 9 + 12p^2}{4p^2}}+\sqrt{\frac{(p^2 - 3)^2}{4p^2}} =\\ & = \sqrt{\frac{(p^2 + 3)^2}{4p^2}}+\sqrt{\frac{(p^2 -3)^2}{4p^2}}=\frac{p^2 + 3}{2p}+\frac{p^2 - 3}{2p}= p.\end{aligned}\] Pri predposlednej úprave sme využili podmienku \(p \geq \sqrt{3}\) (a teda aj \(p^2 -3 \geq 0\) a \(p > 0\)), takže \(\sqrt{(p^2 - 3)^2} = p^2 - 3\) a \(\sqrt{4p^2} = 2p\).
Poznámka. Namiesto skúšky stačí overiť, že pre nájdené \(x\) sú všetky umocňované výrazy nezáporné, teda vlastne stačí overiť, že \[p^2 - 2x - 3 =\frac{(p^2 - 3)(p^2 + 3)}{2p^2}\geq 0.\] Pre \(p \geq \sqrt{3}\) to tak naozaj je.
Vynechať skúšku možno aj takouto úvahou: Funkcia \(\sqrt{x + 3}+\sqrt{x}\) je zrejme rastúca, v bode 0 (ktorý je krajným bodom jej definičného oboru) nadobúda hodnotu \(\sqrt{3}\) a zhora je neohraničená. Preto každú hodnotu \(p \geq \sqrt{3}\) nadobúda pre práve jedno \(x \geq 0\). Z toho vyplýva, že pre \(p \geq \sqrt{3}\) má zadaná rovnica práve jedno riešenie, a teda (jediné) nájdené riešenie [eq:B60S1] musí vyhovovať.
Komentár
Úloha nie je algebraicky náročná, vyžaduje však starostlivú diskusiu definičného oboru, ktorý potom vyústi v obmedzenie hodnôt parametra \(p\). Dôležitou súčasťou riešenia je v tomto prípade aj skúška správnosti, prípadne diskusia, ktorá je uvedená v závere prezentovaného riešenia ̇Úloha 59-II-1
Riešenie*
Iné riešenie*. Položme \(a = n^{k+2} - n^k = n^k (n^2 - 1) = (n - 1)n^k (n + 1)\). Opäť ukážeme, že \(a\) je deliteľné štyrmi a tromi. Ak je \(n\) párne, je \(n^k\) deliteľné štyrmi pre každé celé \(k \geq 2\). Ak je \(n\) nepárne, sú činitele \(n - 1\) a \(n + 1\) párne čísla, takže \(a\) je deliteľné štyrmi pre každé celé \(n = 2\).
Deliteľnosť tromi je zrejmá pre \(n = 3l\). Ak \(n = 3l + 1\), pričom \(l\) je celé kladné číslo, je tromi deliteľný činiteľ \(n - 1\) (a teda aj číslo \(a\)). Ak \(n = 3l + 2\) (\(l\) je celé nezáporné), je tromi deliteľný činiteľ \(n + 1\). Keďže iné možnosti pre zvyšok čísla \(n\) po delení tromi nie sú, je číslo \(a\) deliteľné tromi. Tým je požadovaný dôkaz ukončený.
Komentár
Deliteľnosť štyrmi je tiež možné dokázať aj rozborom možností \(n=4l\), \(n=4l+1\), \(n=4l+2\) a \(n=4l+3\), pre \(l\) celé a nezáporné. Kľúčovým krokom v riešení bolo vhodné rozloženie čísla \(a\) na súčin. To však súdiac podľa priemerného počtu bodov udelených za túto úlohu v krajských kolách1 na Slovensku bola úloha pre riešiteľov neľahká.3,0 b v prípade úspešných riešiteľov, 1,8 b v prípade všetkých riešiteľov, najmenej zo všetkých úloh krajského kola daného ročníka↩︎
Úloha 59-I-6-D1
Riešenie*
Úloha 66-I-6
Riešenie*
Poznámka. Za správne riešenie možno uznať aj riešenie pomocou kalkulačky. Ak majú totiž byť za desatinnou čiarkou dve deviatky, musí byť číslo \(n\) veľmi blízko zľava k nejakej druhej mocnine. Preto stačí na kalkulačke vyskúšať čísla \(\sqrt{3}, \sqrt{8}, \sqrt{15}\) atď. Keďže \(51^2 = 2601\), nájdeme, že \(\sqrt{2600} = 50,990 195\ldots\)
Úloha 66-I-2-D1
Riešenie*
Komentár
Úloha využíva vhodnú úpravu výrazu \(V\) na súčin. Tu študenti zúročia zručnosti nadobudnuté v algebraických seminároch. Zároveň využijú skôr dokázané tvrdenie o deliteľnosti ôsmimi a napokon, úloha ich pripraví na nasledujúci komplexnejší problém.Úloha 59-II-2
Riešenie*
Iné riešenie*. Pri označení \(m = a^2 +1\) a \(n = b^2 +1\) možno ľavú stranu dokazovanej nerovnosti prepísať na tvar \(L = mn-(m-2a)(n-2b) = 2an+2bm-2ab-2ab,\) z ktorého vynímaním dostaneme \(L = 2a(n - b) + 2b(m - a)\).
Čísla \(a, b\) sú z intervalu \(\langle 1, \infty)\), preto \(1 = m - a^2 \leq m - a\). Odtiaľ \(2b(m - a) \geq 2\). Analogicky dostaneme \(2a(n - b) \geq 2\). Teda \(L \geq 4\) a rovnosť nastáva práve vtedy, keď \(a = b = 1\).
Iné riešenie*. Po substitúcii \(a = 1 + m\) a \(b = 1 + n\), pričom \(m, n \geq 0\), získa ľavá strana nerovnosti tvar \[L = (m^2 + 2m + 2)(n^2 + 2n + 2) - m^2 n^2.\] Po roznásobení, ktoré si stačí iba predstaviť, sa zruší člen \(m^2 n^2\), takže \(L\) bude súčtom nezáporných členov, medzi ktorými bude aj člen \(2 \cdot 2 = 4\). Tým je nerovnosť \(L \geq 4\) dokázaná. A keďže medzi spomenutými členmi budú aj \(4m\) a \(4n\), z rovnosti \(L = 4\) vyplýva \(m = n = 0\), čo naopak rovnosť \(L = 4\) tiež zrejme zaručuje. To znamená, že rovnosť nastáva práve vtedy, keď \(a = b = 1\).
Úloha 63-II-1
Riešenie*
Záver. Nájdenému \(x\) zodpovedá trojica cifier \(a = b = c = 9\). Úloha má jediné riešenie.
Komentár
Úloha prináša zaujímavú myšlienku zjednodušenia zápisu, ktorý potom vedie k riešeniu jednoduchej lineárnej rovnice. Aj napriek tomu, že riešenie nevyžaduje mnoho počítania, ukrýva úloha záludnosť v podobe toho, že študenti môžu prísť k správnemu riešeniu nesprávnymi úvahami. Viac o tejto konkrétnej úlohe a jej úskaliach je možné nájsť v článku (Štěpánková 2015), ktorý považujeme za hodný preštudovania.Štěpánková, Hana. 2015. “O Záludnosti Jedné úlohy Z Mo.” Matematika – Fyzika – Informatika 24: 331–34.
Úloha 61-I-2-N3
Riešenie*
Úloha 61-I-1-N4
Riešenie*
Úloha 59-S-1
Riešenie*
Iné riešenie*. Označme \(a/b\) pôvodný zlomok. Zo vzťahov \[\frac{1}{20}=\frac{1}{4\cdot 5} \ \ \ \ \text{a} \ \ \ \ \frac{1}{12}=\frac{1}{4\cdot 3}=\frac{2}{4\cdot 6}\] možno odhadnúť, že riešením by mohlo byť \(b = 4\). Potom \[\frac{4(a + 1) - 5a}{4 \cdot 5}=\frac{1}{20} \ \ \ \ \text{a} \ \ \ \ \frac{4(a + 2) - 6a}{4 \cdot 6}=\frac{1}{12},\] čiže \(a = 3\). Musíme sa však ešte presvedčiť, že úloha iné riešenie nemá. Podmienky úlohy vedú ku vzťahom \[\frac{b - a}{b(b + 1)}=\frac{1}{4\cdot 5} \ \ \ \ \text{a} \ \ \ \ \frac{2(b - a)}{b(b + 2)}=\frac{2}{4\cdot 6}.\] Z podielu ich ľavých a pravých strán potom vyplýva \[\frac{b + 2}{b + 1}=\frac{6}{5},\] čomu vyhovuje jedine \(b = 4\).
Poznámka. V úplnom riešení nesmie chýbať vylúčenie možnosti \(b \neq 4\). Napríklad z podobných rovností \(1/20 = 30/(24 \cdot 25)\) a \(1/12 = 52/(24 \cdot 26)\) by sme mohli hádať, že \(b = 24\), čo riešením nie je.
Úloha B-59-I-5-D1
Riešenie
Úloha 59-I-6-N3
Riešenie*
Úloha 58-I-4-D1
Riešenie*
Úloha 61-I-2
Riešenie*
V našej úlohe je najdlhšia strana trojuholníka rozdelená na úseky, ktorých dĺžky označíme \(3x\) a \(4x\); dĺžku úsekov z vrcholu oproti najdlhšej strane označíme \(y\) (obr. 1). Strany trojuholníka majú teda dĺžky \(7x\), \(4x + y\) a \(3x + y\), kde \(x\), \(y\) sú neznáme kladné čísla (dĺžky berieme bez jednotiek). Ak má byť \(7x\) dĺžka najdlhšej strany, musí platiť \(7x > 4x + y\), čiže \(3x > y\). Zdôraznime, že hľadané čísla \(x, y\) nemusia byť nutne celé, podľa zadania to však platí o číslach \(7x\), \(4x + y\) a \(3x + y\).

Údaj o obvode trojuholníka zapíšeme rovnosťou \[72 = 7x + (3x + y) + (4x + y), \ \ \ \ \text{čiže} \ \ \ \ 36 = 7x + y.\] Pretože \(7x\) je celé číslo, je celé i číslo \(y = 36 - 7x\); a pretože podľa zadania i čísla \(4x + y\) a \(3x + y\) sú celé, je celé i číslo \(x = (4x + y) - (3x + y)\). Preto od tohto okamihu už hľadáme dvojice celých kladných čísel \(x\), \(y\), pre ktoré platí \[3x > y \ \ \ \ \text{a} \ \ \ \ 7x + y = 36.\] Odtiaľ vyplýva \(7x < 36 < 7x + 3x = 10x\), teda \(x \leq 5\) a súčasne \(x \geq 4\).
Pre \(x = 4\) je \(y = 8\) a \((7x, 4x+y, 3x+y) = (28, 24, 20)\), pre \(x = 5\) je \(y = 1\) a \((7x, 4x+ + y, 3x + y) = (35, 21, 16)\). Strany trojuholníka sú teda \((28, 24, 20)\) alebo \((35, 21, 16)\). (Trojuholníkové nerovnosti sú zrejme splnené.)
Úloha 57-I-4-N1
Riešenie*
Úloha B-65-I-3-N2
Riešenie*
Úloha B-58-I-2-D2
Riešenie*
Úloha 57-I-2-N1
Riešenie*
Úloha 58-I-3
Riešenie*
(i) Číslo \(n\) má tvar \(aabb\), kde \(a\), \(b\) sú rôzne cifry. Takže \(n = 1100a + 11b\) a \(\overline{n} = 1100b + 11a\). Číslo 7 má deliť ako \(n\), tak \(\overline{n}\), teda aj ich rozdiel \(n - \overline{n} = 1089(a - b)\) a súčet \(n + \overline{n} = 1111(a + b)\). Keďže ani číslo 1089, ani číslo 1111 nie sú násobkom siedmich a sedem je prvočíslo, tak \(7 \mid a -\)b aj \(7 \mid a + b\). Ak použijeme rovnakú úvahu ešte raz, vidíme, že \(7 \mid (a - b) + (a + b) = 2a\) a \(7 \mid (a + b) - (a - b) = 2b\), teda \(7 \mid a\) a \(7 \mid b\), čiže \(a, b \in \{0, 7\}\). Cifry \(a, b\) sú navzájom rôzne, preto jedna z nich musí byť 0. Ale potom jedno z čísel \(aabb\), \(bbaa\) nie je štvorciferné. Hľadané číslo \(n\) teda nemôže mať uvedený tvar.
(ii) Číslo \(n\) má tvar \(abab\). Potom \(7 \mid n = 1010a + 101b\) a tiež \(7 \mid \overline{n} = 1010b + 101a\). Podobne ako v predchádzajúcom prípade odvodíme, že \(7 \mid n - \overline{n} = 909(a - b)\) a \(7 \mid n + \overline{n} = 1111(a + b)\), a z rovnakých dôvodov ako v predchádzajúcom prípade zisťujeme, že \(7 \mid a\), \(7 \mid b\). Niektorá z cifier by teda musela byť 0. Číslo \(n\) tak nemôže mať ani tvar \(abab\).
(iii) Číslo \(n\) má tvar \(abba\). Potom otočením poradia cifier vznikne to isté číslo, takže máme jedinú podmienku \(7 \mid 1001a + 110b\). Keďže \(7 \mid 1001\) a \(7 \nmid 110\), je táto podmienka ekvivalentná s podmienkou \(7 \mid b\). Preto \(b \in \{0, 7\}\), \(a \in \{1, 2,\,\ldots, 9\}\), \(a \neq b\). Vyhovuje tak všetkých 17 čísel, ktoré práve uvedené podmienky spĺňajú: 1001, 2002, 3003, 4004, 5005, 6006, 7007, 8008, 9009, 1771, 2772, 3773, 4774, 5775, 6776, 8778, 9779.
Úloha 61-I-1
Riešenie*
Dodajme k tomu, že nájdené zvyšky \(c - b + a\) a \(c - 2b + 4a\) sú zrejme rovné hodnotám \(p(-1)\), resp. \(p(-2)\), čo je v zhode s poznatkom, že akýkoľvek mnohočlen \(q(x)\) dáva pri delení dvojčlenom \(x - x_0\) zvyšok rovný číslu \(q(x_0)\).
Podľa zadania platí \(c - b + a = 2\) a \(c - 2b + 4a = 1\). Tretia rovnica \(a + b + c = 61\) je vyjadrením podmienky \(p(1) = 61\). Získanú sústavu troch rovníc vyriešime jedným z mnohých možných postupov.
Z prvej rovnice vyjadríme \(c = b - a + 2\), po dosadení do tretej rovnice dostaneme \(a + b + (b - a + 2) = 61\), čiže \(2b = 59\). Odtiaľ \(b = 59/2\), čo po dosadení do prvej a druhej rovnice dáva \(a+c = 63/2\), resp. \(c+4a = 60\). Ak odčítame posledné dve rovnice od seba, dostaneme \(3a = 57/2\), odkiaľ \(a = 19/2\), takže \(c = 63/2 - 19/2 = 22\). Hľadaný trojčlen je teda jediný a má tvar \[p(x) =\frac{19}{2} \cdot x^2+\frac{59}{2}\cdot x + 22 = \frac{19x^2 + 59x + 44}{2}.\]
Úloha 63-S-2
Riešenie*
Ak zvolíme napríklad \(a = 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 = 720\) a \(b = 1 \cdot 7 \cdot 8 \cdot 9 \cdot 10 = 5040\), bude najmenší spoločný násobok oboch čísel práve \(5040\). Tým je ukázané, že \(5040\) je naozaj najmenšia zo všetkých možných hodnôt \(n\).
I keď bolo úlohou nájsť iba jeden príklad, pre úplnosť uvedieme všetky rozdelenia s minimálnou hodnotou \(n = 5040\):
| Prvá skupina čísel | Druhá skupina čísel |
|---|---|
| 2, 3, 4, 5, 6 | 1, 7, 8, 9, 10 |
| 3, 5, 6, 8 | 1, 2, 4, 7, 9, 10 |
| 2, 5, 8, 9 | 1, 3, 4, 6, 7, 10 |
| 1, 2, 3, 4, 5, 6 | 7, 8, 9, 10 |
| 1, 3, 5, 6, 8 | 2, 4, 7, 9, 10 |
| 1, 2, 5, 8, 9 | 3, 4, 6, 7, 10 |
| 2, 3, 4, 5, 6, 7 | 1, 8, 9, 10 |
| 3, 5, 6, 7, 8 | 1, 2, 4, 9, 10 |
| 2, 5, 7, 8, 9 | 1, 3, 4, 6, 10 |
| 1, 2, 3, 4, 5, 6, 7 | 8, 9, 10 |
| 1, 3, 5, 6, 7, 8 | 2, 4, 9, 10 |
| 1, 2, 5, 7, 8, 9 | 3, 4, 6, 10 |
Nájsť ich nie je ťažké, keď si uvedomíme, že čísla 1 a 7 môžeme dať do ľubovoľnej z oboch skupín, zatiaľ čo v tej istej skupine spolu nemôžu byť 4 s 8, 5 s 10, 3 s 9 ani 6 s 9; s 8 spolu môže byť práve jedno z párnych čísel 2, 6 a 10. Získame tak iba tri základné rozdelenia (prvé tri riadky tabuľky), z ktorých možno každé štyrmi spôsobmi doplniť číslami 1 a 7.
Poznámka. Úlohu možno vyriešiť aj bez výpočtu súčinu \(a \cdot b\). Deliteľnosť \(n\) číslami \(3^2, 5\) a 7 vyplýva z ich priameho zastúpenia medzi rozdeľovanými číslami, deliteľnosť číslom \(2^4\) z jednoduchej úvahy o rozdelení všetkých piatich párnych čísel: ak nie je číslo 8 vo svojej skupine ako párne jediné, je všetko jasné, v opačnom prípade sú v rovnakej skupine čísla 2, 4 a 6 (aj 10, ale to už ani nepotrebujeme).
Úloha 64-I-6-N2
Riešenie*
Úloha B-57-I-5
Riešenie*
Označme \(x_0\) spoločný koreň oboch rovníc, takže \[ax_0^2+ 2bx_0 + 1 = 0,\ \ \ bx_0^2+ 2ax_0 + 1 = 0.\] Odčítaním oboch rovníc dostaneme \((a - b)(x_0^2- 2x_0 ) = x_0 (a - b)(x_0 - 2) = 0\). Keďže \(a \neq b\) a 0 zrejme koreňom daných rovníc nie je, musí byť spoločným koreňom číslo \(x_0 = 2\). Dosadením do daných rovníc tak dostaneme jedinú podmienku \(4a + 4b + 1 = 0\), čiže \[b = -a -\frac{1}{4}.\]
Diskriminant druhej z daných rovníc je potom \(4a^2 - 4b = 4a^2 + 4a + 1 = (2a + 1)^2\), takže rovnica má dva rôzne reálne korene pre ľubovoľné \(a \neq -\frac{1}{2}\). Podobne diskriminant prvej z daných rovníc je \(4b^2- 4a = 4b^2 + 4b +1 = (2b +1)^2\). Rovnica má teda dva rôzne reálne korene pre ľubovoľné \(b \neq -\frac{1}{2}\), čiže \(a\neq \frac{1}{4}\)
Z uvedených predpokladov však zároveň vyplýva \(a \neq -\frac{1}{4}\) \((b \neq 0)\) a \(a \neq - \frac{1}{8}\) \((a \neq b)\).
Záver. Vyhovujú všetky dvojice \((a, -a - \frac{1}{4})\), kde \(a \in \RR \ \{-\frac{1}{2}, -\frac{1}{4}, -\frac{1}{8}, 0, \frac{1}{4}\}\).
Komentár
V úlohe sa k správnemu riešeniu dostaneme pomocou vhodného odčítania dvoch rovníc (a potom vhodnou úpravou takto vzniknutej rovnice). Považujeme za vhodné študentov na tento upozorniť, keďže nájde uplatnenie nielen v nasledujúcej úlohe, ale aj v rôznych iných príkladoch.Úloha B-66-II-1
Riešenie*
Úlohe teda vyhovuje nekonečne veľa dvojíc prirodzených čísel tvaru \((a, b) = (k, k)\), pričom \(k\) je ľubovoľné prirodzené číslo, a keďže číslo \(66 = 2\cdot 3\cdot 11\) má osem deliteľov, tak aj osem dvojíc \((a, b) \in \{\)\((1, 66)\), \((2, 33)\), \((3, 22)\), \((6, 11)\), \((11, 6)\), \((22, 3)\), \((33,2)\), \((66,1)\)\(\}\).
Komentár
Úloha je relatívne jednoduchá a vhodná ako rozcvička na začiatok seminára. Pripomenie študentom metódu riešenia rovníc rozkladom na súčin výrazov, ktorý je rovný nule. Zároveň v záverečnej diskusii zľahka využijú vedomosti o deliteľnosti prirodzených čísel.Úloha 63-II-3
Riešenie
Iné riešenie*. Bez ujmy na všeobecnosti predpokladajme, že \(0 < b \leq a\) (dané vzťahy sa výmenou čísel \(a\) a \(b\) nemenia). Nerovnosť \(c^2 +ab \leq ac+bc\) je ekvivalentná s nerovnosťou \((a - c)(c - b) \geq 0\), takže stačí dokázať, že \(b \leq c \leq a\). Platí \[c^2 = b^2+ a^2 - ab = b^2+ a(a - b) \geq b^2,\] teda \(b \leq c\). Analogicky zistíme, že \[c^2= a^2+ b^2 - ab =a^2+ b(b - a) \leq a^2,\] a odtiaľ \(c \leq a\). Tým je dôkaz prevedený.
Úloha B-60-I-1-N3
Riešenie*
Úloha 65-I-1-D1
Riešenie*
Úloha B-57-S-2
Riešenie*
Rozoberieme dve možnosti:
Ak \(a = b\), majú obidve dané rovnice rovnaký tvar \(x^2 + 4ax + 4a = 0\). Aspoň jeden koreň (samozrejme spoločný) existuje práve vtedy, keď je diskriminant \(16a^2-16a\) nezáporný, teda \(a \in (-\infty, 0\rangle \cup \langle 1, \infty)\).
Ak \(x_0 = -2\), dostaneme z prvej aj z druhej rovnice \(4-2a-2b = 0\), teda \(b = 2-a\). Dosadením do zadania dostaneme rovnice \[x^2 + (2a + 2)x + 4a = 0, \ \ \ \ x^2 + (6-2a)x + 8-4a = 0,\] ktoré majú pri ľubovoľnej hodnote parametra \(a\) spoločný koreň \(-2\).
Záver. Dané rovnice majú aspoň jeden spoločný koreň pre všetky dvojice \((a, a)\), kde \(a \in (-\infty, 0\rangle \cup \langle 1, \infty)\), a pre všetky dvojice tvaru \((a, 2-a)\), kde \(a\) je ľubovoľné.
Úloha 62-I-5
Riešenie*
Upravme najskôr výraz \(V = 2n^3 - 3n^2 + n + 3\) nasledujúcim spôsobom: \[V = (n^3 - 3n^2+ 2n) + (n^3 - n) + 3 = (n - 2)(n - 1)n + (n - 1)n(n + 1) + 3.\] Oba súčiny \((n-2)(n-1)n\) a \((n-1)n(n+1)\) v upravenom výraze \(V\) sú deliteľné tromi pre každé celé číslo \(n\) (v oboch prípadoch sa jedná o súčin troch po sebe idúcich celých čísel), takže výraz \(V\) je pre všetky celé čísla \(n\) deliteľný tromi. Hodnota výrazu \(V\) je preto prvočíslom práve vtedy, keď \(V = 3\), teda práve vtedy, keď súčet oboch spomenutých súčinov je rovný nule: \[0 = (n - 2)(n - 1)n + (n - 1)n(n + 1) = n(n - 1)[(n - 2) + (n + 1)] = n(n - 1)(2n - 1).\] Poslednú podmienku však spĺňajú iba dve celé čísla \(n\), a to \(n = 0\) a \(n = 1\). Tým je úloha vyriešená.
Poznámka. Fakt, že výraz \(V\) je deliteľný tromi pre ľubovoľné celé \(n\), môžeme odvodiť aj tak, že doňho postupne dosadíme \(n = 3k\), \(n = 3k + 1\) a \(n = 3k + 2\), pričom \(k\) je celé číslo, rozdelíme teda všetky celé čísla \(n\) na tri skupiny podľa toho, aký dávajú zvyšok po delení tromi.
Komentár
Aj keď vzorové riešenie môže vyzerať trikovo, po vyskúšaní niekoľko málo hodnôt \(n\) je vždy hodnota zo zadania deliteľná 3, čo by študentov mohlo priviesť na myšlienku skúsiť dokázať deliteľnosť čísla zo zadania tromi.Poznámka. Fakt, že výraz \(V\) je deliteľný tromi pre ľubovoľné celé \(n\), môžeme odvodiť aj tak, že doňho postupne dosadíme \(n = 3k\), \(n = 3k + 1\) a \(n = 3k + 2\), pričom \(k\) je celé číslo, rozdelíme teda všetky celé čísla \(n\) na tri skupiny podľa toho, aký dávajú zvyšok po delení tromi.
Úloha 61-S-2
Riešenie*

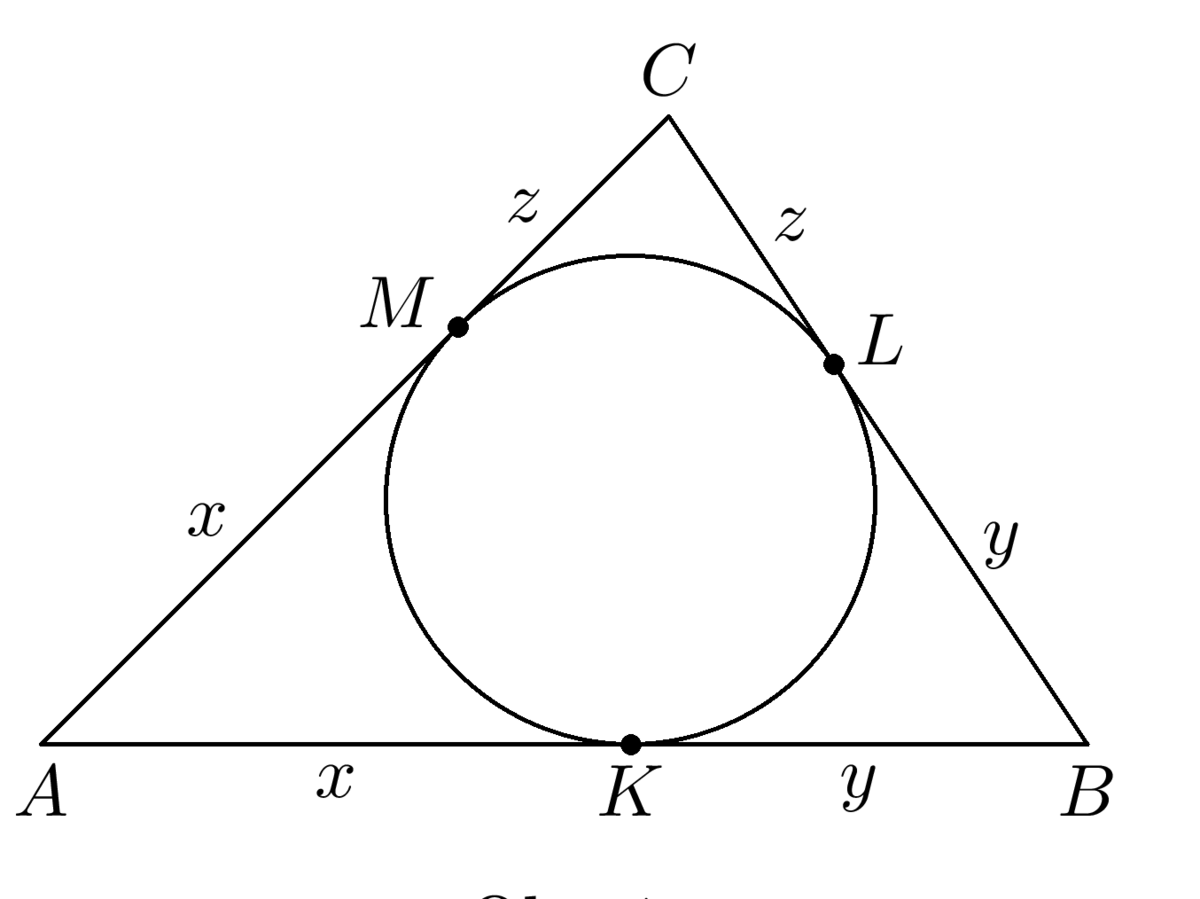
Vzhľadom na symetriu dotyčníc z daného bodu k danej kružnici platia rovnosti \[|SD| = |SE| = |SF| = x \ \ \ \ \text{a} \ \ \ \ |CD| = |CG| = |CH| = y.\] Úsečka \(EF\) má preto dĺžku \(2x\), ktorá je podľa zadania zároveň dĺžkou úsečiek \(AE\) a \(BF\), a teda aj dĺžkou úsečiek \(AG\) a \(BH\) (opäť vďaka symetrii dotyčníc). Odtiaľ už bezprostredne vyplývajú rovnosti \[|AB| = 6x, \ \ \ \ |AC| = |BC| = 2x + y \ \ \ \ \text{a} \ \ \ \ |CS| = x + y.\]
Závislosť medzi dĺžkami \(x\) a \(y\) zistíme použitím Pytagorovej vety pre pravouhlý trojuholník \(ACS\) (s odvesnou \(A\) dĺžky \(3x\)): \[(2x + y)^2= (3x)^2+ (x + y)^2.\] Roznásobením a ďalšími úpravami odtiaľ dostaneme (\(x\) a \(y\) sú kladné hodnoty) \[\begin{aligned}
4x^2+ 4xy + y^2 &= 9x^2+ x^2+ 2xy + y^2,\\
2xy & = 6x^2,\\
y &= 3x.\end{aligned}\] Hľadaný pomer tak má hodnotu \[|AB| : |CS| = 6x : (x + y) = 6x : 4x = 3 : 2.\] Poznamenajme, že prakticky rovnaký postup celého riešenia možno zapísať aj pri štandardnom označení \(c = |AB|\) a \(v = |CS|\). Keďže podľa zadania platí \(|AE| =\frac{1}{3}c\), a teda \(|SE| =\frac{1}{6}c\), z rovnosti \(|SD| = |SE|\) vyplýva \(|CD| = |CS|-|SD| = v-\frac{1}{6}c\), odkiaľ \[|AC| = |AG| + |CG| = |AE| + |CD| =\tfrac{1}{3}c + (v-\tfrac{1}{6}c) = v~+\tfrac{1}{6}c,\] takže z Pytagorovej vety pre trojuholník \(ACS\), \[(v +\tfrac{1}{6}c)^2= (\tfrac{1}{2}c)^2+ v^2,\] vychádza \(3v = 2c\), čiže \(c : v~= 3 : 2\).
Komentár
Úloha vychádza z poznatku, ktorý si študenti osvojili v úlohe predchádzajúcej a pridáva k nemu ešte prácu s Pytagorovou vetou a manipuláciu s algebraickými výrazmi, takže tvorí prirodzené pokračovanie úlohy predchádzajúcej.Úloha 64-I-2-N6
Riešenie*
Úloha 59-I-5-N1
Riešenie*
Úloha 59-I-3-N2
Riešenie
Úloha 59-I-5-D1
Riešenie*
Úloha 66-I-1-D1
Riešenie*
Úloha 63-I-6-N4
Riešenie*
Úloha 58-I-1
Riešenie*
Žiadny chlapec nemohol dostať 8 Sk zároveň od druhého aj od piateho okoloidúceho (inak by mal aspoň 16 Sk, najviac však mohol každý z chlapcov dostať 12 Sk). Takže od druhého a piateho majú traja chlapci po 8 Sk a jeden od nich nedostal nič. Najviac jeden z týchto troch chlapcov mohol dostať 4 Sk od štvrtého okoloidúceho, inak by mali už aspoň dvaja chlapci aspoň 12 Sk. Štvrtý okoloidúci musel teda dať 4 Sk práve jednému z nich a 4 Sk zostávajúcemu chlapcovi. Bez peňazí prvého a tretieho okoloidúceho teda majú chlapci vybraných 12, 8, 8 a 4 Sk. Chlapec, ktorý dostal v súčte od druhého, štvrtého a piateho okoloidúceho dvanásť korún, už nemohol dostať od prvého a tretieho okoloidúceho nič, lebo by mal viac ako dvanásť korún. Ten, ktorý dostal v súčte od druhého, štvrtého a piateho okoloidúceho 4 Sk, musel dostať od prvého a tretieho v súčte maximálnu možnú čiastku, t. j. \(3+2 = 5\) Sk, inak by mal dokopy menej ako 9 Sk (dostal teda práve 9 Sk a vyzbieral najmenej). Takže najmenej vyzbieral Tomáš, lebo on dostal od prvého okoloidúceho 3 Sk, a najviac Peter, ktorý od prvého okoloidúceho nedostal nič.
Úvahy ľahko dokončíme a ukážeme, že popísané rozdelenie je skutočne možné. Ako už vieme, Tomáš vyzbieral 9 Sk a Peter 12 Sk. Jakub, ktorý dostal 2 Sk od prvého, nemohol dostať od tretieho nič, takže dostal celkom 10 Sk, a Martin 11 Sk. Všetky úvahy môžeme prehľadne usporiadať do tabuľky, ktorú postupne dopĺňame.
| 1 | 2 | 3 | 4 | 5 | \(\Sigma\) |
|---|---|---|---|---|---|
| 8 | 0 | 0 | |||
| 0 | 0 | 8 | |||
| 0 | 0 | 0 | 4 | 8 | 12 \(\rightarrow\) P |
| 3 | 0 | 2 | 4 | 0 | \(\leq 9 \rightarrow\) T |
| \(1+2+3\) | \(1 \times 8\) | \(2\times 2\) | \(2 \times 4\) | \(2 \times 8\) |
Úloha B-58-I-5-N1
Riešenie*
Úloha 65-I-5-D1
a) Dokážte, že medzi vybranými číslami sú najviac štyri deliteľné tromi.
b) Ukážte, že vybraných čísel môže byť 26.
Riešenie*
Úloha 64-I-2-N4-N5
Riešenie*
Úloha 62-I-1-N2, upravené
Riešenie*
Komentár
Ako sme už spomínali, táto úloha je tiež prípravou na domácu prácu. Je tiež vhodným miestom, kde môžeme prípadným tápajúcim študentom pripomenúť metódu riešenia, s ktorou sme sa už stretli: pokúsiť sa vypozorovať, ako sa úloha správa pre menšie rozmery, napr. tabuľku \(3\times 3\) a potom objavené výsledky zovšeobecniť.Úloha 64-I-1-N1
a) \(|x| = x + 2 \ \ [x = -1]\)
b) \(|2x + 2| = x + 4 \ \ [x = -2, x = 2]\)
c) \(|x - 1| = |x| - 1 \ \ [x = 1]\)
Riešenie*
Úloha 61-I-4-N6
Riešenie*
Úloha 63-I-2
Riešenie*

na priamku \(AT\) v bode \(T\) s osou uhla ohraničeného priamkou \(p\) a polpriamkou \(BA\). Jej polomer bude mať veľkosť \(|ST|\).
Ostáva zostrojiť vrchol \(C\) hľadaného trojuholníka \(ABC\). Ten bude ležať jednak na priamke \(p\), jednak na druhej dotyčnici vpísanej kružnice z vrcholu \(A\), ktorá je súmerne združená so stranou \(AB\) podľa priamky \(AS\). Stačí teda zostrojiť bod \(U\) dotyku strany \(AC\) s kružnicou vpísanou ako obraz bodu \(T\) v uvedenej osovej súmernosti.
Odtiaľ vyplýva konštrukcia:
\(p\): \(P \in p\) a \(p \perp AP\);
\(B\): \(B \in AT \cap p\), bod \(B\) musí ležať na polpriamke \(AT\) za bodom \(T\);
\(q\): \(T \in q\) a \(q \perp AT\);
\(u_1\), \(u_2\): dve (navzájom kolmé) osi rôznobežiek \(AB\), \(p\);
\(S_1\), \(S_2\): \(S_1 \in q \cap u_1\), \(S_2 \in q \cap u_2\);
\(U_1\), \(U_2\): obrazy bodu \(T\) v súmernostiach podľa priamok \(AS_1\) a \(AS_2\);
\(C_1\), \(C_2\): priesečníky priamky \(p\) s polpriamkami \(AU_1\) a \(AU_2\);
trojuholníky \(ABC_1\) a \(ABC_2\).
Diskusia. Bod \(B\) konštruovaný v 2. kroku existuje, len ak uhol \(PAT\) je ostrý (inak ani polpriamka \(AT\) nepretne priamku \(p\)) a zároveň bod \(T\) leží vnútri polroviny \(pA\), čo je ekvivalentné s tým, že aj uhol \(APT\) je ostrý. Body \(S_1\), \(S_2\) existujú vždy a sú rôzne, lebo ležia v opačných polrovinách určených priamkou \(AB\). Kružnica vpísaná leží celá v trojuholníku \(ABC\), a teda i v páse určenom priamkou \(p\) a priamkou s ňou rovnobežnou, ktorá prechádza vrcholom \(A\), takže stred \(S\) vpísanej kružnice musí padnúť do pásu tvoreného priamkou \(p\) a priamkou \(p'\) s ňou rovnobežnou, ktorá rozpoľuje výšku \(AP\). V takom prípade dotyčnica ku kružnici \((S; |ST|)\) (súmerne združená s dotyčnicou \(AB\) podľa priamky \(AS\)) určite pretne priamku \(p\) v hľadanom vrchole \(C\).
Diskusiu zhrnieme takto: Ak pre vnútorné uhly trojuholníka \(APT\) platí \(|\measuredangle PAT| \geq 90^\circ\) alebo \(|\measuredangle APT| \geq 90^\circ\), nemá úloha riešenie. Ak platí \(|\measuredangle PAT| < 90^\circ\) a zároveň \(|\measuredangle APT| < 90^\circ\), je počet riešení 0 až 2 podľa toho, koľko zo zostrojených bodov \(S_1\) a \(S_2\) leží medzi rovnobežkami \(p\) a \(p'\).
Komentár
V posledných rokoch sa v MO nevyskytlo veľké množstvo konštrukčných úloh. Napriek tomu však považujeme za dôležité vyriešiť so študentmi aspoň jeden takýto problém a poukázať na to, že zostrojením vyhovujúceho útvaru riešenie úlohy nekončí a je potrebné uviesť aj diskusiu, ktorá je častokrát aspoň tak náročná ako vhodná konštrukcia. Zaradenie úlohy v tomto seminári považujeme za vhodné tiež preto, lebo úloha využíva vlastnosti kružnice vpísanej, a tak so cťou uzavrie toto seminárne stretnutie.Úloha 66-I-5-N3
Riešenie*
Úloha B-65-I-3-N1
Riešenie*
Úloha 64-S-2
Riešenie*
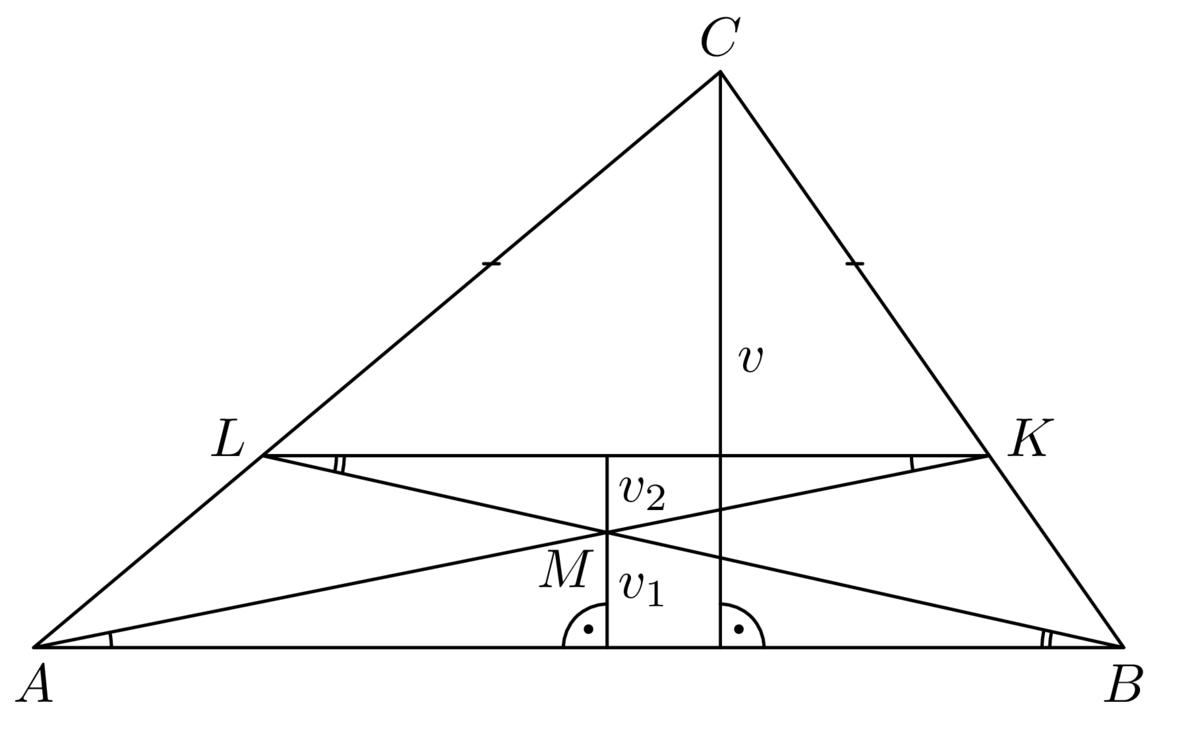
Keďže \(|KL| =\frac{2}{3}|AB|\), je tiež \(v_2 =\frac{2}{3}v_1\), a preto \(v_1 + v_2 =\frac{5}{3}v_1\), čiže \[v = 3(v_1 + v_2) = 5v_1.\] Trojuholníky \(ABM\) a \(ABC\) majú spoločnú stranu \(AB\), preto ich obsahy sú v pomere výšok na túto stranu, takže obsah trojuholníka \(ABC\) je päťkrát väčší ako obsah trojuholníka \(ABM\).
Komentár
Ďalšia úloha, ktorá precvičuje rovnaké tvrdenie ako predchádzajúca. Pomery výšok je tentoraz potrebné určiť z podobnosti trojuholníkov. Tu sa teda uplatnia znalosti precvičované na minulom seminárnom stretnutí.Úloha 57-II-4
Riešenie*
V prvom prípade po dosadení \(x = z\) do pôvodnej rovnice dostaneme \(z-y =\sqrt{3}(z- y)\). Odtiaľ \(z = y = x\).
V druhom prípade, keď \(y = z\), dôjdeme analogicky k rovnakému výsledku.
Záver. Riešením danej rovnice sú všetky trojice \((x, y, z) = (k, k, k)\), kde \(k\) je ľubovoľné celé číslo.
Komentár
Aj napriek tomu, že vzorové riešenie úlohy vyzerá zrozumiteľne, úloha riešiteľov krajských kôl potrápila (bola najhoršie hodnotenou úlohou daného krajského kola). Záludnosti sa ukrývajú vo vytyčovaní iracionálnych čísel a nie neznámych, vhodnej úprave rovnice a diskusii o (i)racionalite oboch strán rovnice.Úloha 62-I-1-N1
Riešenie*
Pri inom postupe je možné rozdeliť všetky cesty podľa toho, koľko pri nich urobí kobylka skokov dĺžky dva (ich počet môže byť 0, 1, 2, 3, 4 alebo 5 a tým je tiež určený počet skokov dĺžky \(1\): 10, 8, 6, 4, 2 alebo 0). Ku každému takému počtu potom určíme počet všetkých rôznych poradí jednotiek a dvojok (dávajúcich v súčte 10). Dostaneme tak \(1+9+28+ 35 + 15 + 1 = 89\) možných ciest.
Komentár
Úloha opäť pravdepodobne nebude pre študentov neprekonateľnou výzvou. Bude však určite zaujímavé sledovať, ako sa študenti popasujú s hľadaním počtu spôsobov. Taktiež úloha slúži ako príprava na úlohu nasledujúcu a domácu prácu.Úloha 58-I-6-D2
Riešenie*
Úloha 59-I-4-N2
Riešenie*
Úloha 59-I-6-N1
Riešenie
Komentár
Úloha je v porovnaní s tým, čo v seminárnom stretnutí nasleduje, jednoduchá, osvieži však študentom často používanú myšlienku: číslo \(\overline{abc}\) môžeme zapísať v tvare \(100a+10b+c\). Tú využijeme v mnohých ďalších úlohách.Úloha 66-I-1
Riešenie*
Iné riešenie*. Danú nerovnosť môžeme prepísať na tvar \[(a^2 - a + 1) + \frac{1}{a^2-a+1}\geq 2 \ \ \ \ \text{čiže} \ \ \ \ u~+\frac{1}{u}\geq 2,\] pričom \(u = a^2 -a + 1\). Využitím faktu, že posledná nerovnosť platí pre každé kladné reálne číslo \(u\) a že prechádza v rovnosť jedine pre \(u = 1\).
Na dôkaz pôvodnej nerovnosti ostáva už len overiť, že výraz \(u = a^2 - a + 1\) je kladný pre každé reálne číslo \(a\). To možno spraviť rovnako ako v prvom riešení, alebo prepísať nerovnosť \(a^2 - a + 1 > 0\) na tvar \[a(a -1) > -1\] a uskutočniť krátku diskusiu: Posledná nerovnosť platí ako pre každé \(a \geq 1\), tak pre každé \(a\leq 0\), lebo v oboch prípadoch máme dokonca \(a(a - 1) \geq 0\); pre zvyšné hodnoty \(a\), teda pre \(a \in (0, 1)\), je súčin \(a(a - 1)\) síce záporný, avšak určite väčší ako \(-1\), pretože oba činitele \(a\), \(a - 1\) majú absolútnu hodnotu menšiu ako 1. Prepísaná nerovnosť je tak dokázaná pre každé reálne číslo \(a\), a tým je podmienka pre použitie nerovnosti \(u + \frac{1}{u} \geq 2\) pre \(u = a^2 + a + 1\) overená.
Ako sme už uviedli, rovnosť \(u + \frac{1}{u} = 2\) nastane jedine pre \(u = 1\). Pre rovnosť v nerovnosti zo zadania úlohy tak dostávame podmienku \(a^2 -a+1 = 1\), čiže \(a(a-1)= 0\), čo je splnené iba pre \(a = 0\) a pre \(a = 1\).
Komentár
Úloha využíva spojenie viacerých poznatkov – faktu, že druhá mocnina akéhokoľvek reálneho čísla je nezáporná, úpravu na štvorec, ekvivalentné úpravy nerovností a tiež známu nerovnosť \(u+\frac{1}{u} \geq 2\) pre každé kladné reálne \(u\). Je síce náročnejšia ako úlohy, ktorými sme sa doteraz zaoberali, ale považujeme ju za vhodnú ilustráciu toho, ako nám rozšírený arzenál metód pomôže v úspešnom zvládnutí zložitejších problémov. Úloha tiež demonštruje, že k správnemu riešeniu častokrát vedú viaceré cesty.Úloha 65-I-6-N1
Riešenie
Úloha 66-I-5
Riešenie*

[fig:66I5_2]
a \(MNC\) sú navzájom podobné (podľa vety \(sus\)), platí \(|AB| : |KL| : |MN| = |AC| : |KC| : |MC| = 3 : 2 : 1\). Podľa zhodných vnútorných uhlov spomenutých troch trojuholníkov platí tiež \(AB \parallel KL\), \(KL \parallel MN\). Štvoruholníky \(ABLK\), \(KLNM\) a \(ABNM\) tak sú naozaj lichobežníky (ako je prezradené v zadaní) so základňami \(AB\), \(KL\) a \(MN\), ktorých dĺžky sú v už odvodenom pomere \(3 : 2 : 1\). Navyše predĺžené ramená všetkých troch lichobežníkov sa pretínajú v bode \(C\), ktorým preto podľa dokázanej vlastnosti prechádzajú priamky \(S_1 S_2\), \(S_2 S_3\) (a \(S_1 S_3\)), takže ide o jednu priamku, na ktorej body \(S_1\), \(S_2\), \(S_3\) a \(C\) ležia v uvedenom poradí tak, že \(|S_1 C| : |S_2 C| : |S_3 C| = 3 : 2 : 1\). Z toho vyplýva \(|S_1 S_2 | = |S_2 S_3 | (= |S_3 C|)\), takže bod \(S_2\) je stredom úsečky \(S_1 S_3\). Na nej (opäť podľa dokázaného tvrdenia) ležia aj body \(E\), \(F\) a \(G\), pričom pre bod \(E\) medzi bodmi \(S_1\), \(S_2\) platí \(|ES_1 | : |ES_2 | = 3 : 2\), pre bod \(F\) medzi bodmi \(S_2\), \(S_3\) platí \(|FS_2| : |FS_3| = 2 : 1\) a napokon pre bod \(G\) medzi bodmi \(S_1\), \(S_3\) platí \(|GS_1| : |GS_3 | = 3 : 1\). Tieto delenia troch úsečiek sme znázornili na obr. [fig:66I5_3], kam sme zapísali aj dĺžky vzniknutých úsekov pri voľbe jednotky \(1 = |S_1 S_2 | = |S_2 S_3 |\) (pri ktorej \(|S_1 S_3 | = 2\)).
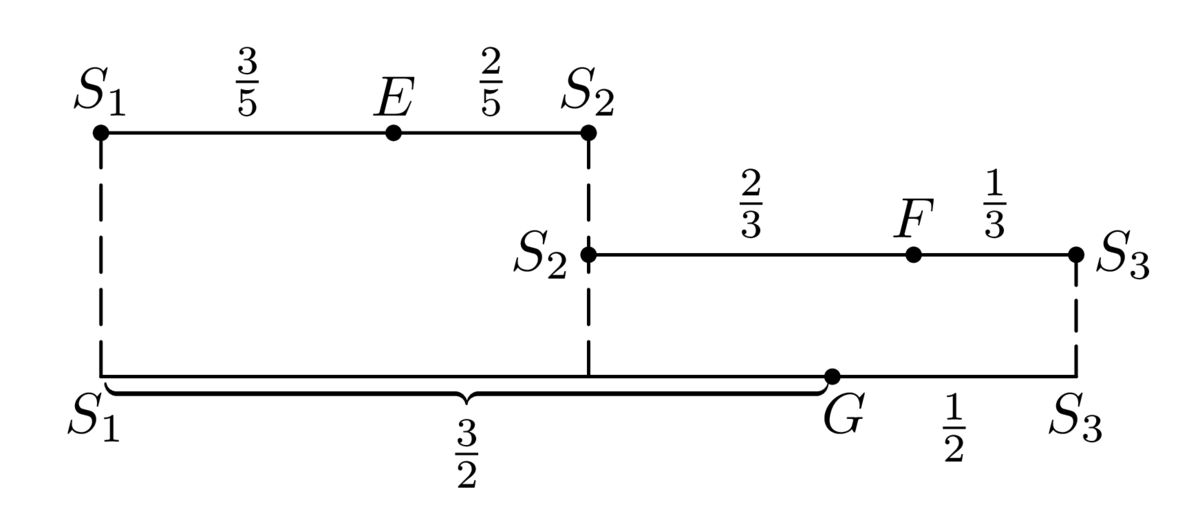
[fig:66I5_3]
Keďže \[|S_1 F| = |S_1 S_2 | + |S_2 F| = 1 +\frac{2}{3}=\frac{5}{3}>\frac{3}{2}= |S_1 G|,\] platí \(|GF| = |S_1 F| - |S_1 G| =\frac{5}{3} -\frac{3}{2}=\frac{1}{6}\), čo spolu s rovnosťou \(|EF| = |ES_2 | + |S_2 F|=\frac{2}{5}+\frac{2}{3}=\frac{16}{15}\) už vedie k určeniu hľadaného pomeru \[|GF| : |EF| =\frac{1}{6}:\frac{16}{15}= 5 : 32.\]
Komentár
Úloha je zložitejšia ako predchádzajúca, ale študenti zoznámení s prípravnou úlohou, zbehlí vo využívaní podobných trojuholníkov a precízni, aby sa nestratili v záverečnom pomerovaní, by si s úlohou poradiť mali.Úloha 57-II-1
Riešenie*
Zrejme \[\label{eq:57II1_1} a= y + z, \ \ \ \ b = z~+ x, \ \ \ \ c = x + y.\] Z uvedených rovností vidíme, že daná podmienka \[\label{eq:57II1_2} b + c < 3a\] je ekvivalentná nerovnosti \[\label{eq:57II1_3} x < y + z,\] čo je nutná podmienka existencie trojuholníka so stranami dĺžok \(x\), \(y\) a \(z\).
Dosadením z [eq:57II1_1] do podmienok \(b \leq c\) a \(a \leq b\) zistíme, že \(z \leq y\) a \(y \leq x\). To znamená, že ďalšie dve trojuholníkové nerovnosti \(y < z~+ x\) a \(z < x + y\) sú automaticky splnené, takže nerovnosť [eq:57II1_3], a tým aj [eq:57II1_2] je podmienkou postačujúcou. Tým je tvrdenie úlohy dokázané.
Komentár
Úloha využíva poznatok, že spojnice vrcholov a bodov dotyku so stredom vpísanej kružnice rozdelia trojuholník na tri dvojice zhodných trojuholníkov. Ten využijeme v nasledujúcej úlohe aj domácej práci. Okrem toho, aj keď úloha nie je na výpočet nijako extrémne náročná, je študentov potrebné upozorniť, že dokazujú ekvivalenciu, takže nerovnosť zo zadania musí byť nielen podmienkou nutnou, ale aj postačujúcou.Úloha 60-I-5
Riešenie*
Iné riešenie*. Označme \(d = (a, b)\), takže \(a = ud\) a \(b = vd\) pre nesúdeliteľné prirodzené čísla \(u, v\). Z toho hneď vieme, že \([a, b] = uvd\). Keďže \[\begin{aligned} a \cdot (a, b) + b \cdot [a, b]& = ud^2+ uv^2d^2= u(1 + v^2)d^2,\\ 2ab& = 2uvd^2,\end{aligned}\] je vzhľadom na \(ud^2 > 0\) nerovnosť zo zadania ekvivalentná s nerovnosťou \(1 + v^2 \geq 2v\), čiže \((v - 1)^2 \geq 0\), čo platí pre každé \(v\). Rovnosť nastane práve vtedy, keď \(v = 1\), čiže \(b \mid a\).
Iné riešenie*. Označme \(d = (a, b)\). Je známe, že \([a, b] \cdot (a, b) = ab\). Po vyjadrení \([a, b]\) z tohto vzťahu, dosadení do zadanej nerovnosti a ekvivalentnej úprave dostaneme ekvivalentnú nerovnosť \(d^2 + b^2 \geq 2bd\), ktorá platí, lebo \((d - b)^2 \geq 0\). Rovnosť nastáva pre \(d = b\), čiže v prípade \(b \mid a\).
Komentár
Na úspešné zvládnutie úlohy je opäť potrebná znalosť z predchádzajúceho seminára o nerovnostiach a taktiež ponúka široké spektrum prístupov, takže bude zaujímavé sledovať, ako k nej študenti pristúpia.Úloha 62-S-2
Riešenie*
Z poslednej rovnosti je zrejmé, že môže byť jedine \(k = 2\) alebo \(k = 1\).
Pre \(k = 2\) vychádza \(l = d = 1\), čomu zodpovedá dvojica \(a = 2\), \(b = 1\).
Pre \(k = 1\) dostávame rovnicu \(ld = 4\), ktorá má v obore kladných celých čísel tri riešenia:
\(l = 4\), \(d = 1\) a riešením úlohy je dvojica \(a = 1\), \(b = 4\);
\(l = 2\), \(d = 2\) a riešením úlohy je dvojica \(a = 2\), \(b = 4\);
\(l = 1\), \(d = 4\) a riešením úlohy je dvojica \(a = 4\), \(b = 4\).
Záver. Úlohe vyhovujú práve štyri dvojice kladných celých čísel \((a, b)\), a to (2, 1), (1, 4), (2, 4) a (4, 4).
Iné riešenie*. Využijeme známu rovnosť \([a, b] \cdot (a, b) = a \cdot b\), ktorá platí pre všetky celé kladné \(a\), \(b\). Vynásobením oboch strán danej rovnice číslom [a, b] tak dostaneme \[a[a, b]^2= 4ab, \ \ \ \text{čiže} \ \ \ [a, b]^2= 4b. \ \ \ \todo{ (1)}\]
Vzhľadom na to, že \([a, b] \geq b\), a teda \[4b = [a, b]^2 \geq b^2,\] je \(b^2\leq 4b\), takže \(b \leq 4\). Navyše z upravenej rovnice vyplýva, že \(4b\), a teda aj \(b\) je druhou mocninou celého čísla. Preskúmaním oboch prípadov \(b \in \{1, 4\}\) (dosadíme do pôvodnej rovnice postupne všetky možné hodnoty \((a, b)\), ktorých je konečne veľa, alebo dosadíme do a využijeme to, že \(a\) je deliteľom najmenšieho spoločného násobku \([a, b]\)) dôjdeme k rovnakému záveru ako v prvom riešení.
Iné riešenie*. Keďže zrejme platí \([a, b] = (a, b)\), vyplýva zo zadanej rovnosti nerovnosť \(a \leq 4\), pričom rovnosť \(a = 4\) nastane práve vtedy, keď \([a, b] = (a, b)\) čiže \(a = b = 4\). To je prvé riešenie danej úlohy, pri všetkých ostatných musí byť \(a = 1\), \(a = 2\), alebo \(a = 3\). Pre \(a = 1\) máme rovnicu \(1 \cdot b = 4\), takže \((a, b) = (1, 4)\) je druhým riešením. Pre \(a = 2\) máme rovnicu \(2[2, b] = 4(2, b)\) čiže \([2, b] = 2(2, b)\), odkiaľ podľa možných hodnôt \((2, b) = 1\) a \((2, b) = 2\) dostaneme \(b = 1\), resp. \(b = 4\); ďalšie dve (tretie a štvrté) riešenia teda sú \((a, b) = (2, 1)\) a \((a, b) = (2, 4)\). Napokon pre \(a = 3\) máme rovnicu \(3[3, b] = 4(3, b)\), z ktorej vyplýva \(3 \mid (3, b)\), čiže \(3 \mid b\), takže máme vlastne rovnicu \(3b = 12\), ktorej jediné riešenie \(b = 4\) však podmienku \(3 \mid b\) nespĺňa.
Poznámka. Diskusii o prípade \(a = 3\) sa možno vyhnúť nasledujúcou úvahou. Prepíšme zadanú rovnicu na tvar \[\frac{[a, b]}{(a, b)}=\frac{4}{a}.\] Keďže zlomok na ľavej strane je zrejme celé číslo, musí byť taký aj zlomok na pravej strane, takže a je jedno z čísel 1, 2 alebo 4.
Úloha 64-I-5-N3
Riešenie
Úloha 63-I-4-N5
Riešenie*
Úloha 65-I-1-N1
Riešenie*
Úloha 62-I-2-D3
Riešenie*
Úloha 62-S-3
Riešenie*
Úloha 65-I-5
Riešenie*
Všimnime si najskôr, že pre súčet s ľubovoľných dvoch daných čísel platí \(11 = 5 + 6 \leq s \leq 55 + 54 = 109\). Medzi číslami od 11 po 109 sú palindrómy práve všetky násobky 11 a navyše aj číslo 101. Uvedomme si teraz, že deliteľnosť súčtu dvoch čísel daným číslom \(d\) (nám pôjde o hodnotu \(d = 11\)) závisí iba na zvyškoch oboch sčítaných čísel po delení dotyčným \(d\). Toto užitočné pravidlo uplatníme tak, že všetky dané čísla od 5 po 55 rozdelíme do skupín podľa ich zvyškov po delení číslom 11 a tieto skupiny zapíšeme do riadkov tak, aby súčet dvoch čísel z rôznych skupín na rovnakom riadku bol deliteľný číslom 11; o význame zátvoriek na konci každého riadku budeme hovoriť vzápätí.
\[\begin{aligned} \{5, 16, 27, 38, 49\}&, \ \ \ \{6, 17, 28, 39, 50\} &\text{(5 čísel)},\\ \{7, 18, 29, 40, 51\}&, \ \ \ \{15, 26, 37, 48\} &\text{(5 čísel)},\\ \{8, 19, 30, 41, 52\}&, \ \ \ \{14, 25, 36, 47\} &\text{(5 čísel)},\\ \{9, 20, 31, 42, 53\}&, \ \ \ \{13, 24, 35, 46\} &\text{(5 čísel)},\\ \{10, 21, 32, 43, 54\}&, \ \ \ \{12, 23, 34, 45\} &\text{(5 čísel)}\\ \{11, 22, 33,& 44, 55\} \ \ &\text{(1 číslo)}.\end{aligned}\]
Na koniec každého riadku sme pripísali maximálny počet na ňom zapísaných čísel, ktoré môžeme súčasne vybrať bez toho, aby súčet dvoch z nich bol násobkom čísla 11. Napríklad v treťom riadku máme päticu čísel so zvyškom 8 a štvoricu čísel so zvyškom 3. Je jasné, že nemôžeme súčasne vybrať po čísle z oboch týchto skupín (ich súčet by bol násobkom 11), môžeme však vybrať súčasne všetkých päť čísel z pätice (súčet každých dvoch z nich bude po delení 11 dávať taký istý zvyšok ako súčet 8 + 8, teda zvyšok 5). Dodajme ešte, že uvedená schéma šiestich riadkov má pre nás ešte jednu obrovskú výhodu: súčet žiadnych dvoch čísel z rôznych riadkov nie je násobkom 11 (tým totiž nie je ani súčet ich dvoch zvyškov).
Z uvedeného rozdelenia všetkých daných čísel do šiestich riadkov vyplýva, že vyhovujúcim spôsobom nemôžeme vybrať viac ako \(5 \cdot 5 + 1 = 26\) čísel. Keby sme však vybrali 26 čísel, muselo by medzi nimi byť aj jedno z čísel 49 alebo 50 a z ďalších štyroch riadkov postupne čísla 51, 52, 53 a 54 – potom by sme ale dostali palindróm 49 + 52 alebo 50 + 51. A tak sa nedá vybrať viac ako 25 čísel, pritom výber 25 čísel možný je: z prvých piatich riadkov vyberieme napríklad všetky čísla z ľavých skupín s výnimkou čísla 52 a k tomu jedno číslo (napríklad 11) z posledného riadku. Potom súčet žiadnych dvoch vybraných čísel nebude deliteľný 11 (vďaka zaradeniu čísel do skupín), ani rovný poslednému ”kritickému“ číslu, palindrómu 101 (preto sme pri voľbe čísla 49 vylúčili 52).
Odpoveď. Najväčší možný počet kartičiek, ktoré môžeme požadovaným spôsobom vybrať, je rovný číslu 25. Iné riešenie. Medzi vybranými číslami môžu byť
iba jedno číslo z pätice (11, 22, 33, 44, 55);
nanajvýš jedno číslo z každej z 20 nasledujúcich dvojíc (5, 6), (7, 15), (8, 14), (9, 13), (10, 12), (16, 17), (18, 26), (19, 25), (20, 24), (21, 23), (27, 28), (29, 37), (30, 36), (31, 35), (32, 34), (38, 39), (40, 48), (41, 47), (42, 46) a (43, 45);1
nanajvýš dve čísla zo štvorice (49, 50, 51, 52) (pretože súčty 49 + 50, 50 + 51 a 49 + 52 sú palindrómy);
obe zvyšné čísla 53 a 54.
Preto sa nedá požadovaným spôsobom vybrať viac ako 1 + 20 + 2 + 2 = 25 čísel. Vyhovujúci výber 25 čísel je možný: jedno číslo z pätice násobkov 11, menšie z dvoch čísel z každej z 20 dvojíc, čísla 49 a 51 zo štvorice a napokon obe čísla 53 a 54. Je však nutné vysvetliť, prečo súčet žiadnych dvoch vybraných čísel nie je násobkom 11 (prečo nie je rovný 101, je zrejmé hneď). Na to si stačí všimnúť, že menšie čísla z 20 dvojíc dávajú po delení jedenástimi postupne zvyšky, ktoré sa opakujú s periódou dĺžky 5 majúcou zloženie (5, 7, 8, 9, 10), napokon posledné štyri vybrané čísla majú postupne zvyšky 5, 7, 9 a 10, takže súčet žiadnych dvoch zvyškov nami vybraných čísel naozaj nie je násobkom 11. (Zhodou okolností sa jedná o rovnaký príklad vyhovujúceho výberu 25 čísel ako v prvom riešení.)
Tieto dvojice so súčtami deliteľnými číslom 11 sme vytvorili postupne zo zvyšných čísel tak, že sme k najmenšiemu doposiaľ nezapísanému číslu sme pripojili ďalšie najmenšie doposiaľ nezapísané číslo, ktoré ”dopľňa“ prvé číslo na nejaký násobok 11. Takému postupu sa najmä v matematickej informatike hovorí pažravý algoritmus.↩︎
Úloha 61-I-5
Riešenie*

Z pravouhlého trojuholníka \(BSA\) pomocou Pytagorovej vety vyjadríme veľkosť \(v\) výšky \(AS\), pričom v pravouhlom trojuholníku \(BSO\) s preponou dĺžky \(R\) pre odvesnu \(OS\) platí \(|OS| =||AS|-|AO|| = |v-R|\) (musíme si uvedomiť, že v tupouhlom trojuholníku \(ABC\) bude bod \(S\) ležať medzi bodmi \(A\) a \(O\)!). Dostávame tak dve rovnosti \[\begin{aligned} v^2 &= b^2 -\frac{a^2}{4},\\ R^2 &= \frac{a^2}{4}+ (v~-R)^2;\end{aligned}\] ich sčítaním vyjde \[v^2+ R^2= b^2 + (v~- R)^2,\ \ \ \ \text{čiže} \ \ \ \ b^2= 2vR.\] Dosadením z prvej rovnice \(v =\frac{1}{2}\sqrt{4b^2- a^2}\) do poslednej rovnosti dostaneme hľadaný vzorec pre \(R\).
Dodajme, že rovnosť \(b^2 = 2vR\), ktorú sme práve odvodili a z ktorej už ľahko vyplýva vzorec pre polomer \(R\), je Euklidovou vetou o odvesne \(AB\) pravouhlého trojuholníka \(ABA'\) s preponou \(AA'\), ktorá je priemerom kružnice opísanej trojuholníku \(ABC\) (obr. 1).
Nájdený vzorec pre polomer \(R\) zapíšeme prehľadne spolu s druhým hľadaným vzorcom pre polomer \(r\), ktorého odvodeniu sa ešte len budeme venovať: \[\label{eq:61I5} R =\frac{\sqrt{b^2}}{\sqrt{4b^2 - a^2}}\ \ \ \ \text{a}\ \ \ \ r = \frac{a\sqrt{4b^2-a^2}}{2(a+2b)}.\] Druhý zo vzorcov [eq:61I5] sa dá získať okamžite zo známeho vzťahu \(r = 2S/(a + b + c)\) pre polomer \(r\) kružnice vpísanej do trojuholníka so stranami \(a\), \(b\), \(c\) a obsahom \(S\); v našom prípade stačí len dosadiť \(b = c\) a \(2S = av\), kde \(v = \frac{1}{2}\sqrt{4b^2 - a^2}\) podľa úvodnej časti riešenia.
Ďalšie dva spôsoby odvodenia druhého zo vzorcov [eq:61I5] založíme na úvahe o pravouhlom trojuholníku \(AMP\), ktorého strany majú dĺžky \[|AM| = v~-r, \ \ \ \ |MP| = r, \ \ \ \ |AP| = |AC| - |PC| = b - |SC| = b - \frac{a}{2}.\] Pre tento trojuholník môžeme napísať Pytagorovu vetu alebo využiť jeho podobnosť s trojuholníkom \(ACS\), konkrétne zapísať rovnosť sínusov ich spoločného uhla pri vrchole \(A\). Podľa toho dostaneme rovnice \[(v - r)^2= r^2+\big(b -\frac{a}{2}\big)^2, \ \ \ \ \text{resp.} \ \ \ \ \frac{r}{v-r}= \frac{\frac{1}{2}a}{b},\] ktoré sú obidve lineárne vzhľadom na neznámu \(r\) a majú riešenie \[r = \frac{v}{2}-\frac{1}{2v}\cdot \big( b - \frac{a}{2} \big)^2, \ \ \ \ \text{resp.}\ \ \ \ r=\frac{av}{a+2b}.\] Po dosadení za \(v\) v oboch prípadoch dostaneme hľadaný vzorec pre \(r\). V druhom prípade je to zrejmé, v prvom to ukážeme: \[\begin{aligned}
r & =\frac{v}{2} - \frac{1}{2v} \cdot \bigg(b -\frac{a}{2}\bigg)^2= \frac{v^2 - b^2 + ab- \frac{1}{4}a^2}{2v}=\frac{2ab - a^2}{4v}=\\
& = \frac{a(2b - a)}{2\sqrt{(2b -a)(2b + a)}}=\frac{a\sqrt{2b-a}}{2\sqrt{2b+a}} =\frac{a \sqrt{4b^2 -a^2}}{2(a + 2b)}.\end{aligned}\] Ešte ostáva dokázať nerovnosť \(R \geq 2r\). Využijeme na to odvodené vzorce [eq:61I5], z ktorých dostávame (pripomíname, že \(2b > a > 0\)) \[\frac{R}{2r}= R \cdot \frac{1}{2r}=\frac{b^2}{\sqrt{4b^2-a^2}}\cdot \frac{a+2b}{a \sqrt{4b^2-a^2}}=\frac{b^2}{a(2b-a)}.\] Nerovnosť \(R \geq 2r\) teda platí práve vtedy, keď \(b^2\geq a(2b -a)\). Posledná nerovnosť je však ekvivalentná s nerovnosťou \((a - b)^2\geq 0\), ktorej platnosť je už zrejmá. Tým je dôkaz nerovnosti \(R \geq 2r\) hotový. Navyše vidíme, že rovnosť v nej nastane jedine v prípade, keď \((a - b)^2 = 0\), čiže \(a = b\), teda práve vtedy, keď je pôvodný trojuholník nielen rovnoramenný, ale dokonca rovnostranný.
Komentár
Úloha poskytuje mnoho prístupov k riešeniu a bude zaujímavé nechať študentov porovnať ich výsledky. Spája tiež zistenia z predchádzajúcich úloh, v niektorých prípadoch študenti využijú Euklidovu vetu a nezaobídu sa ani bez zručnej manipulácie s algebraickými výrazmi.Úloha 66-I-6-N2
Riešenie*
Úloha 62-I-4-N5
Riešenie*
Úloha 66-I-6-D1
Riešenie*
Úloha 61-II-1
Riešenie*
Iné riešenie*. Podľa vzorca pre druhú mocninu trojčlena platí \[(x - y + z)^2= x^2+ y^2+ z^2 - 2xy + 2xz - 2yz.\] Dosaďme to do pravej strany dokazovanej nerovnosti a urobme niekoľko ďalších ekvivalentných úprav: \[\begin{aligned}
x^2 - y^2+ z^2 &> x^2+ y^2+ z^2 - 2xy + 2xz - 2yz,\\
0 &> 2y^2 - 2xy + 2xz - 2yz,\\
0 &> 2y(y - x) + 2z(x - y),\\
0 &> 2(y - x)(y - z).\end{aligned}\] Posledná nerovnosť už vyplýva z predpokladov úlohy, podľa ktorých je činiteľ \(y - x\) kladný, zatiaľ čo činiteľ \(y - z\) je záporný.
Komentár
Úloha sa dá vyriešiť jednoduchým použitím ekvivalentných úprav a diskusiou v závere, v ktorej je potrebné nezabudnúť na predpoklady z úvodu zadania. Ak študenti sami neprídu na dôkaz pomocou použitia vzorca \(A^2-B^2\), je vhodné im ho ukázať, keďže tak budeme demonštrovať viacero odlišných prístupov k riešeniu úlohy. Zároveň úloha nevyžaduje špeciálne vedomosti a je tak príjemným prepojením tohto a minulého seminára o nerovnostiach.Úloha 65-II-4
Riešenie*
Ak začína Barbora, môže Adam hrať tak, aby vyšiel zlomok s menovateľom \(10c+d\) deliteľným tromi, ktorého čitateľ \(10a + b\) však deliteľný tromi nebude. Na to Adamovi stačí po každom z oboch Barboriných ťahov vhodne čitateľ či menovateľ, napríklad podľa kritéria deliteľnosti tromi mu stačí zabezpečiť, aby sa ciferný súčet \(a+b\) čitateľa rovnal 10 a aby sa ciferný súčet \(c+d\) menovateľa rovnal 9 alebo 12. Adam tak vyhrá, pretože výsledný zlomok nebude možné krátiť tromi, takže sa nebude rovnať žiadnemu zlomku s mocninou čísla 10 v menovateli, akým sa dá zapísať každé číslo s konečným počtom desatinných miest.
Komentár
Úlohu je možné najprv zadať ako hru medzi dvoma hráčmi a až po tom, čo študenti odohrajú niekoľko kôl a vypozorujú zákonitosti, je vhodné pustiť sa do tvrdého riešenia. Zaujímavé tiež môže byť porovnať stratégie jednotlivých študentov medzi sebou, príp. ich po samostatnej práci nechať niekoľko súbojov odohrať znova, aby svoju stratégiu overili v praxi.Úloha B-59-I-3-D1
Riešenie*
Úloha 65-I-6-D2
Riešenie*
Úloha 66-I-5-D1
Ukážte, že pomer obsahov trojuholníkov \(ABC\) a \(ABD\) je pre \(p = 2 : 3\) rovnaký ako pre \(p = 3 : 2\).
Zdôvodnite, prečo pomer obsahov trojuholníkov \(ABC\) a \(ABD\) má hodnotu aspoň 4.
Riešenie*
Úloha 58-I-1-D2
Riešenie*
Úloha B-63-II-1
Riešenie*
Ak \(x = y = z\), vyjde dosadením do ktorejkoľvek zo zadaných rovníc \(y^2 + 12y - 85 = 0\) a odtiaľ \(y = 5\) alebo \(y = -17\).
Ak \(x = y\), \(z = 6 - y\), dostaneme z prvej zadanej rovnice \(y^2 + 36 = 85\), a teda \(y = 7\) alebo \(y = -7\).
Ak \(x = 6 - y\), \(z = y\), dostaneme z poslednej zadanej rovnice opäť \(y^2 + 36 = 85\), a teda \(y = 7\) alebo \(y = -7\).
Ak \(x = z = 6 - y\), dostaneme z druhej zadanej rovnice \(y^2 + 6(12 - 2y) = 85\) čiže \(y^2 - 12y - 13 = 0\) a odtiaľ \(y = -1\) alebo \(y = 13\).
Odpoveď. Sústava rovníc má osem riešení, a to \((5, 5, 5)\), \((-17, -17, -17)\), \((7, 7, -1)\), \((-7, -7, 13)\), \((-1, 7, 7)\), \((13, -7, -7)\), \((7, -1, 7)\), \((-7, 13, -7)\).
Úloha 64-I-2-N3
Riešenie*
Úloha B-65-I-3-D2
Riešenie*
Úloha 61-I-1-N1
Riešenie*
Úloha 65-I-5-N1
Riešenie*
Úloha 59-II-4
Riešenie*
a) Pre \(p = 2\) je riešením sústavy ľubovoľné \(x \in \langle 1006, 1007)\) a \(y = 1 004\).
b) Pre \(p = 3\) nemá sústava žiadne riešenie.
Iné riešenie*. Položme \(\lfloor x \rfloor = a\), potom \(x = a + t\), pričom \(t \in \langle 0, 1)\).
a) Pre \(p = 2\) sústavu prepíšeme na tvar \(y = a-2\) a \(\lfloor 2a-2+t \rfloor = 2 010\). Z poslednej rovnice vyplýva \(2a - 2 = 2 010\), odtiaľ \(a = 1 006\). Keďže \(t \in \langle 0, 1)\), vyhovuje pôvodnej sústave každé \(x \in \langle 1006, 1007)\), pričom \(y = 1 004\).
b) Pre \(p = 3\) dostávame \(y = a - 3\) a \(\lfloor 2a - 3 + t\rfloor = 2 010\). Posledná rovnica je ekvivalentná so vzťahom \(2a - 3 = 2 010\), ktorému nevyhovuje žiadne celé číslo \(a\). Pre \(p = 3\) nemá daná sústava rovníc riešenie.
Úloha 61-I-2-N1
Riešenie*
Úloha 60-I-2-D1
Riešenie*
Úloha B-65-S-2
Riešenie*
Bod \(L\), ktorý je vďaka podmienke \(AB \parallel KL\) súmerne združený s \(K\) podľa \(o\), bude preto ležať v polrovine \(oB\), teda \(KL\) a \(AB\) (a teda aj \(DB\)) budú súhlasne orientované rovnobežné úsečky. Z toho vyplýva zhodnosť súhlasných uhlov \(LKF\) a \(BDF\). Spolu tak dostávame \(|\measuredangle LKF| = |\measuredangle BDF| = |\measuredangle BFK|\).
Priamky \(FB\) a \(KL\) sú potom súmerne združené podľa osi úsečky \(FK\), ktorá prechádza stredom \(C\) kružnice \(k\), a je teda aj jej osou súmernosti. Preto aj priesečníky \(B\) a \(L\) týchto priamok s kružnicou \(k\) sú súmerne združené podľa tejto osi, takže štvoruholník \(KLBF\) je rovnoramenný lichobežník, čiže \(|KL| = |BF|\). Spojením s rovnosťou \(|BF|= |BD|\) polomerov kružnice \(m\) tak dostávame požadovanú rovnosť \(|KL| = |BF| = |BD|\).
Úloha 59-I-4-D2
Riešenie*
Úloha 60-I-1-N2
Riešenie*
Úloha 66-S-2
Riešenie*
| \(n\) | \(V (n)\) |
|---|---|
| 1 | 0 |
| 3 | \(168 = 3 \cdot 48 + 24\) |
| 5 | \(888 = 18 \cdot 48 + 24\) |
| 7 | \(2928 = 61 \cdot 48\) |
| 9 | \(7440 = 155 \cdot 48\) |
Medzi hľadané zvyšky teda patria čísla 0 a 24. Ukážeme, že iné zvyšky už možné nie sú. Na to stačí dokázať, že pre každé nepárne číslo \(n\) platí \(24 \mid V~(n)\). Z školskej časti seminára vieme, že pre každé prirodzené číslo \(n\) platí \(12 \mid V~(n)\), teda aj \(3 \mid V~(n)\). Keďže čísla 3 a 8 sú nesúdeliteľné, stačí ukázať, že pre každé nepárne číslo \(n\) platí \(8 \mid V~(n)\). Využijeme pritom rozklad daného výrazu na súčin \[\label{eq:66S2} V (n) = n^4+ 11n^2 - 12 = (n^2 - 1)(n^2+ 12) = (n - 1)(n + 1)(n^2+ 12).\] Ľubovoľné nepárne prirodzené číslo \(n\) možno zapísať v tvare \(n = 2k - 1\), pričom \(k \in \NN\) . Pre také \(n\) potom dostávame \[V (2k - 1) = [(2k - 1) - 1][(2k - 1) + 1][(2k - 1)^2 + 12] = 4(k - 1)k(4k^2 - 4k + 13),\] a keďže súčin \((k - 1)k\) dvoch po sebe idúcich celých čísel je deliteľný dvoma, je celý výraz deliteľný ôsmimi.
Záver. Daný výraz môže dávať po delení číslom 48 práve len zvyšky 0 a 24.
Poznámka. Poznatok, že \(8 \mid V~(n)\) pre každé nepárne \(n\), možno dokázať aj inak, bez použitia rozkladu [eq:66S2]. Ak je totiž \(n = 2k - 1\), pričom \(k \in \NN\) , tak číslo \[n^2= (2k - 1)^2= 4k^2 - 4k + 1 = 4k(k - 1) + 1\] dáva po delení ôsmimi (vďaka tomu, že jedno z čísel \(k\), \(k - 1\) je párne) zvyšok 1, a teda rovnaký zvyšok dáva aj číslo \(n^4\) (ako druhá mocnina nepárneho čísla \(n^2\)). Platí teda \(n^2 = 8u + 1\) a \(n^4 = 8v + 1\) pre vhodné celé \(u\) a \(v\), takže hodnota výrazu \[V (2k - 1) = (8v + 1) + 11(8u + 1) - 12 = 8(v + 11u)\] je naozaj násobkom ôsmich.
Pripojme aj podobný dôkaz poznatku \(3 \mid V~(n)\) zo seminárneho stretnutia. Pre čísla \(n\) deliteľné tromi je to zrejmé, ostatné \(n\) sú tvaru \(n = 3k \pm 1\), takže číslo \[n^2= (3k \pm 1)^2= 9k^2 \pm 6k + 1 = 3k(3k \pm 2) + 1\] dáva po delení tromi zvyšok 1, rovnako tak aj číslo \(n^4 = (n^2)^2\). Dosadenie \(n^2 = 3u + 1\) a \(n^4 = 3v + 1\) do výrazu \(V (n)\) už priamo vedie k záveru, že \(3 \mid V~(n)\).
Úloha 60-I-5-N1
Riešenie
Komentár
Táto mini-úloha je prípravným krokom k nasledujúcemu všeobecnejšiemu tvrdeniu a zároveň môže pripomenúť použitie dôkazu sporom.Úloha 64-II-2
Riešenie*
Komentár
Po krátkom experimentovaní by malo byť väčšine študentov jasné, ako sa bude šachovnica správať, a tým pádom aj aká bude odpoveď na otázku zo zadania. (Ne)náročnosti úlohy zodpovedá aj jej bodové hodnotenie v krajskom kole, kde sa stala najlepšie hodnotenou úlohou daného ročníka.1Na Slovensku, s priemerom 3,8 b medzi všetkými riešiteľmi a 5,5 b medzi úspešnými riešiteľmi.↩︎
Úloha 60-S-2
Riešenie*
Obsah lichobežníka vypočítame ako súčin jeho výšky s dĺžkou strednej priečky. Výška je v našom prípade rovná dĺžke strany štvorca čiže 6 cm. Jeho stredná priečka má teda dĺžku 2 cm. Z toho vyplýva, že stred úsečky \(KL\) musí ležať na osi strany \(AB\) vo

[fig:60S2_1]
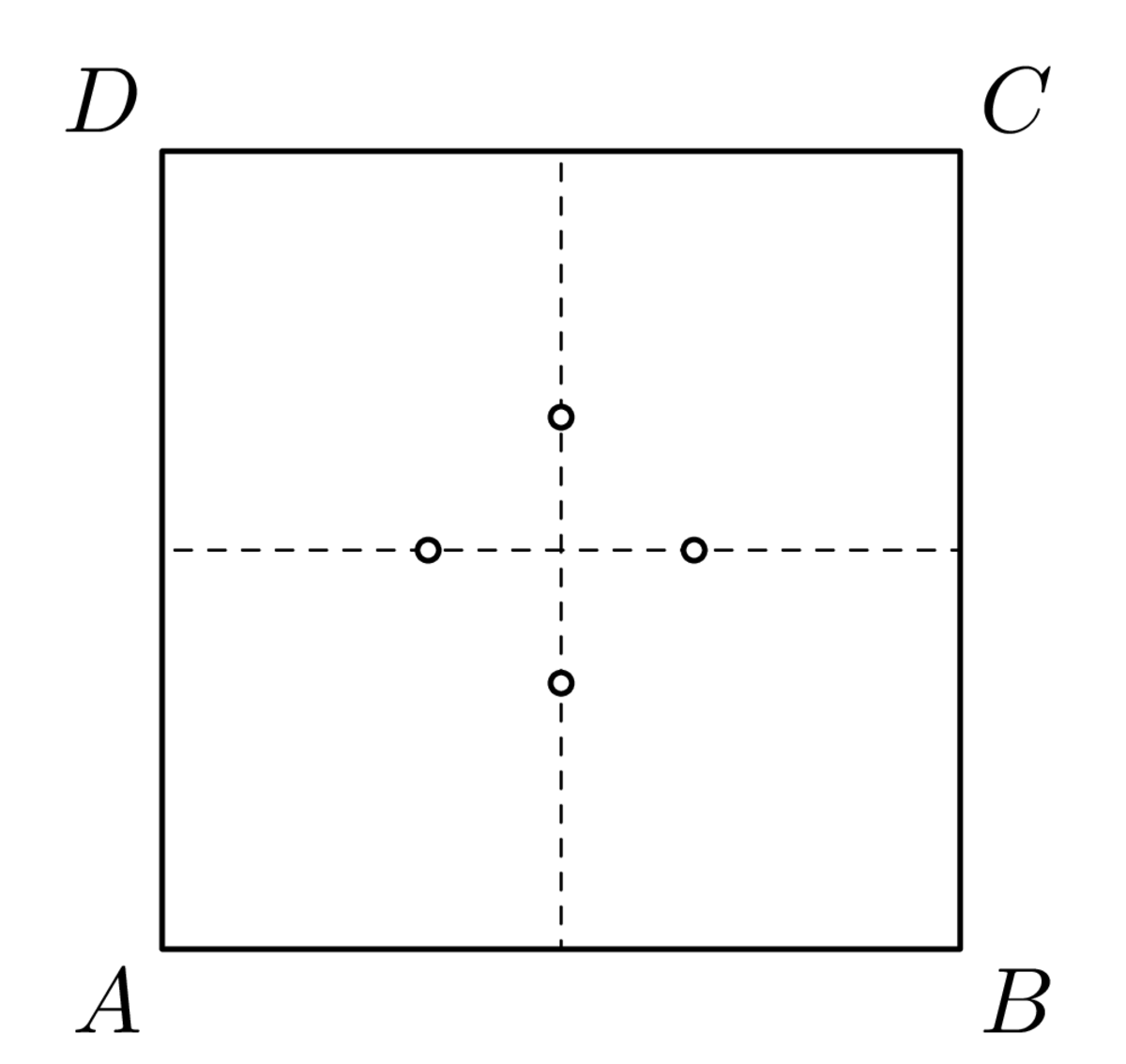
[fig:60S2_2]
vzdialenosti 2 cm od stredu strany \(AB\) (obr. [fig:60S2_1]). Platí to aj naopak: Ak stred úsečky \(KL\) leží v opísanej polohe, bude štvoruholník \(KABL\) lichobežník s obsahom 12 cm\(^2\).
Ak budeme namiesto lichobežníka \(KABL\) uvažovať lichobežník \(KDCL\), vyjde stred priečky \(KL\) na osi úsečky \(CD\) vo vzdialenosti 2 cm od stredu strany \(CD\).
Ak priečka \(KL\) spája body na stranách \(AB\) a \(CD\), dostaneme ďalšie dva možné body ležiace na spojnici stredov úsečiek \(AD\) a \(BC\). Hľadanú množinu teda tvoria štyri body, ktoré ležia na priečkach spájajúcich stredy protiľahlých strán štvorca vo vzdialenosti 1 cm od jeho stredu (obr. [fig:60S2_2]).
Úloha 57-I-1-D2
Riešenie*
Úloha B-64-S-2
Riešenie*
Trojuholníky \(ABP\) a \(ADP\) majú zhodnú výšku z vrcholu \(A\). Pre pomer ich obsahov preto platí \(S : S_{ADP} = |BP| : |DP|\). Podobne pre trojuholníky \(BCP\) a \(CDP\) dostaneme \(S_BCP : S_{CDP} = |BP| : |DP|\). Z toho už vyplýva \(S : S_{ADP} = S_{BCP} : S_{CDP}\), čo vzhľadom na odvodené vzťahy znamená \[\frac{S}{10}=\frac{8 - S}{1 + S}.\] Po úprave tak dostaneme pre \(S\) kvadratickú rovnicu \[S^2+ 11S - 80 = (S + 16)(S - 5) = 0,\] ktorá má dva korene \(-16\) a \(5\). Keďže obsah \(S\) trojuholníka \(ABP\) je nezáporné číslo, vyhovuje iba \(S = 5\). Odtiaľ už ľahko dopočítame z vyššie uvedených vzťahov \(S_{BCP} = 3\) a \(S_{CDP} = 6\). Obsah celého štvoruholníka \(ABCD\) vyjadrený v cm\(^2\) teda je \[S + S_{BCP} + S_{CDP} + S_{ADP} = 5 + 3 + 6 + 10 = 24.\] Záver. Obsah štvoruholníka \(ABCD\) je 24 cm\(^2\).
Úloha B-66-I-3-N2
Riešenie*
Úloha B-58-II-1
Riešenie*
Záver. Daná sústava rovníc má riešenie iba pre \(a = -1\), a to \(x = 0\), \(y = 1\), \(z = 0\). Skúška pri tomto postupe nie je nutná.
Komentár
Úloha vyžaduje umné narábanie so sústavou troch rovníc tak, aby bolo možné uskutočniť záverečnú diskusiu o existencii riešenia pre rôzne hodnoty parametra \(a\). Je tiež vhodné so študentami prediskutovať, prečo v tomto prípade nie je nutné robiť skúšku správnosti.Úloha 65-S-2
a) Koľko ľudí mohlo sedieť pri stole na začiatku, ak v prvom kole vypadol z hry práve jeden hráč?
b) Mohla mať hra jediného víťaza, teda človeka, ktorý po určitom počte kôl zostal v hre sám?
Riešenie*
Ak sú na začiatku hráči aspoň traja, tak v prvom kole vypadne iba jeden hráč \(A\), keď napríklad hráč \(A\) dá hlas sebe a všetci ostatní (sú najmenej dvaja) ho dajú tomu istému hráčovi \(B\), \(B \neq A\) (teda aj hráč \(B\) dá hlas sebe). Nie je to samozrejme jediný spôsob hlasovania s požadovaným výsledkom.
b) Vysvetlíme, prečo jediný hráč v hre nikdy zostať nemôže. Opak by znamenal, že v poslednom kole pred uvedenou situáciou, keď v hre bolo povedzme m hráčov, pričom \(m > 1\), by v dôsledku ich hlasovania vypadlo \(m - 1\) hráčov. Keďže pri tomto hlasovaní bolo rozdaných práve \(m\) hlasov a \(m - 1\) hráčov (tí, čo potom vypadli) dostalo práve jeden hlas, musel aj zvyšný \(m\)-tý hráč dostať práve jeden (zvyšný) hlas, a teda tiež vypadnúť, a to je spor.
Úloha 62-I-4-N1
Z ľubovoľných 82 prirodzených čísel možno vybrať dve čísla tak, aby ich rozdiel bol deliteľný číslom 81. Dokážte.
Riešenie*
Úloha 64-I-6-N4
Riešenie*
Úloha 65-I-2-N1
Riešenie*
Úloha 59-I-2-D1
Riešenie*
Úloha B-59-I-3-N1
Riešenie
Úloha 61-I-4-N5
Riešenie*
Úloha 65-I-3-D5
Riešenie*
Úloha B-59-II-1
Riešenie*

Úloha B-65-I-3-D1
Riešenie*
Úloha 59-I-5
Riešenie*
Z ľavej nerovnosti odstránime zlomky a umocníme ju na druhú, \[\begin{aligned} 25ab(a^2 + 2ab + b^2) &\leq 4(a^4 + 9a^2 b^2 + b^4 + 6a^3 b + 6ab^3 + 2a^2 b^2),\\ 25ab(a^2 + b^2 ) + 50a^2 b^2 &\leq 4a^4 + 4b^4 + 44a^2 b^2 + 24ab(a^2 + b^2 ),\end{aligned}\] takže po úprave dostaneme ekvivalentnú nerovnosť \[4a^4 + 4b^4 - 6a^2 b^2 \geq ab(a^2 + b^2 ).\] Po odčítaní výrazu \(2a^2 b^2\) od oboch strán nerovnosti sa nám podarí na oboch stranách použiť úpravu na štvorec. Dostaneme tak (opäť ekvivalentnú) nerovnosť \[4(a^2 - b^2 )^2 \geq ab(a - b)^2.\] Rozdiel štvorcov v zátvorke na ľavej strane ešte rozložíme na súčin a vzťah upravíme na tvar \(4(a - b)^2 (a + b)^2 \geq ab(a - b)^2\).
Ak \(a = b\), platí rovnosť. Ak \(a \neq b\), môžeme poslednú nerovnosť vydeliť kladným výrazom \((a - b)^2\) a dostaneme tak nerovnosť \(4(a + b)^2 \geq ab\), čiže \(4a^2 + 4b^2 + 7ab \geq 0\). Ľavá strana tejto nerovnosti je vždy kladná, preto vyšetrovaná nerovnosť platí pre všetky kladné čísla \(a, b\), pričom rovnosť v nej nastane práve vtedy, keď \(a = b\).
Komentár
Táto úloha prvýkrát prináša sústavu nerovností a je vhodné so študentmi zopakovať, ako k dokazovaniu sústav nerovností pristupujeme: musíme dokázať riešenie každej nerovnosti zvlášť. V priebehu riešenia opäť využijeme úpravu na štvorec a nezápornosť druhej mocniny reálneho čísla. Úloha sa dá riešiť ešte iným spôsobom, ten si však ukážeme v ďalšom seminári zameranom na nerovnosti.Úloha 59-I-1
Riešenie*
Komentár
Úloha opäť nevyžaduje žiadne matematické znalosti, je však výbornou previerkou toho, ako sú študenti schopní narábať s veľkým množstvom informácií, nestratiť v nich prehľad a využiť ich na zdarné vyriešenie zadaného problému.Úloha B-60-I-1-N5
Riešenie*
Úloha 60-I-4-N1
Riešenie*
Úloha 62-I-4
Riešenie*
Počet všetkých úsečiek \(A_iA_j\) s krajnými bodmi v ľubovoľne vybranej sedemprvkovej množine vrcholov je \((7 \cdot 6) : 2 = 21 > 19\), takže dve z týchto úsečiek ležia v rovnakej z 19 opísaných skupín. Tým je existencia žiadaného lichobežníka dokázaná, nech už je sedemprvková množina vrcholov zvolena akokoľvek.
Poznámka. Úvodnú úvahu o osi úsečky \(A_iA_j\) možno vynechať. Namiesto toho môžeme rovno opísať uvedených 19 deväťprvkových skupín navzájom rovnobežných úsečiek a potom skonštatovať, že ide o všetky možné úsečky \(A_iA_j\), lebo tých je \((19 \cdot 18) : 2 = 19 \cdot 9\), teda práve toľko, koľko je úsečiek v opísaných 19 skupinách.
Iné riešenie*. Zatiaľ čo v prvom riešení sme uvažovali o základniach hľadaného lichobežníka, teraz sa zameriame na jeho ramená alebo uhlopriečky. V oboch prípadoch to musia byť dve zhodné úsečky, lebo každý lichobežník, ktorému možno opísať kružnicu, je rovnoramenný. Osi jeho základní totiž musia prechádzať stredom opísanej kružnice, takže splývajú a tvoria tak os súmernosti celého lichobežníka. Naopak každé dve tetivy jednej kružnice, ktoré majú rovnakú dĺžku kratšiu ako priemer kružnice, nie sú rovnobežné a nemajú spoločný krajný bod, tvoria buď ramená, alebo uhlopriečky (rovnoramenného) lichobežníka (stačí si uvedomiť, že ľubovoľné dve zhodné tetivy jednej kružnice sú súmerne združené podľa priamky prechádzajúce stredom uvedenej kružnice a priesečníkom prislúchajúcich sečníc).
V pravidelnom 19-uholníku \(A_1A_2\,\ldots A_{19}\) majú zrejme všetky úsečky \(A_iA_j\) dokopy len 9 rôznych dĺžok. Vo vybranej sedemprvkovej množine vrcholov má oba krajné body celkom \((7 \cdot 6) : 2 = 21\) úsečiek. Keďže \(21 > 2 \cdot 9\), podľa Dirichletovho princípu niektoré tri z týchto úsečiek majú rovnakú dĺžku (t. j. sú zhodné). Keby každé dve z týchto troch úsečiek mali spoločný vrchol (a vieme, že z ľubovoľného vrcholu vychádzajú nanajvýš dve zhodné strany či uhlopriečky), vytvorili by tieto tri úsečky rovnostranný trojuholník, čo nie je možné, lebo \(3 \nmid 19\). Preto niektoré dve z týchto troch zhodných úsečiek nemajú spoločný krajný bod, takže to sú buď ramená, alebo uhlopriečky rovnoramenného lichobežníka (protiľahlé strany rovnobežníka to byť nemôžu).
Úloha 58-I-4-N2
Riešenie*
Úloha 58-I-1-N1
Riešenie*
Úloha 61-I-5-N6
Riešenie*
Úloha 66-I-2-D5
Riešenie*
Úloha 62-I-6-D1
Riešenie*
Úloha 60-I-3-N2
Riešenie*
Úloha 66-I-1-D4
Riešenie*
Úloha 57-I-5-N1
Dokážte, že v Skupine nemôže byť trojica osôb, ktoré sa poznajú navzájom (tzv. trojuholník známych), ani osoba, ktorá má aspoň troch známych.
Dokážte, že tu nemôže byť trojuholník neznámych ani osoba, ktorá sa nepozná aspoň s tromi osobami.
Nakreslite graf známostí v takej Skupine osôb.
Riešenie*
Úloha 61-II-4
Riešenie*
V prípade \(n = 6\) všetky prípustné dvojice sú \[(1, 3), (1, 4), (1, 5), (1, 6), (2, 5), (3, 5).\] Z tohto zoznamu ľahko odhalíme, že víťaznú stratégiu má (prvá) hráčka Marína. Ak totiž zotrie na začiatku hry číslo 4, musí Tamara zotrieť číslo 1, a keď potom Marína zotrie číslo 6, nemôže už Tamara žiadne ďalšie číslo zotrieť. Okrem tohto priebehu \(4 \rightarrow 1\rightarrow 6\) si môže Marína zaistiť víťazstvo aj inými, pre Tamaru ”vynútenými“ priebehmi, napríklad \(6\rightarrow 1 \rightarrow 4\) alebo \(4 \rightarrow 1 \rightarrow 3 \rightarrow 5 \rightarrow 2\).
V prípade \(n = 12\) je všetkých prípustných dvojíc výrazne väčšie množstvo. Preto si položíme otázku, či všetky čísla od 1 do 12 možno rozdeliť na šesť prípustných dvojíc. Ak totiž nájdeme takú šesticu, môžeme opísať víťaznú stratégiu druhej hráčky (Tamary): ak zotrie Marína pri ktoromkoľvek svojom ťahu číslo \(x\), Tamara potom vždy zotrie to číslo \(y\), ktoré s číslom \(x\) tvorí jednu zo šiestich nájdených dvojíc. Tak nakoniec Tamara zotrie aj posledné (dvanáste) číslo a vyhrá (prípadne hra skončí skôr tak, že Marína nebude môcť zotrieť žiadne číslo).
Hľadané rozdelenie všetkých 12 čísel do šiestich dvojíc naozaj existuje, napríklad \[(1, 4), (2, 9), (3, 8), (5, 12), (6, 11), (7, 10).\] Iné vyhovujúce rozdelenie dostaneme, keď v predošlom dvojice (1, 4) a (6, 11) zameníme dvojicami (1, 6) a (4, 11). Ďalšie, menej podobné vyhovujúce rozdelenie je napríklad \[(1, 6), (2, 5), (3, 10), (4, 9), (7, 12), (8, 11).\] Záver. Pre \(n = 6\) má víťaznú stratégiu Marína, pre \(n = 12\) Tamara.
Komentár
Úloha je náročnejšia ako predchádzajúca, no študenti by mali prvú časť zvládnuť samostatne, v časti druhej môžu svoje sily spojiť s ďalšími spolužiakmi, príp. stratégie, ktoré vymysleli, otestovať pri vzájomnej hre.Úloha 65-I-2
Riešenie*
Uvedomme si, čo podmienka úlohy hovorí o počte znakov \(N\) pripísaných vrcholom jednej a tej istej steny kocky: počet týchto \(N\) je nanajvýš 2 (súčin troch pripísaných \(N\) by bol totiž nepárny, teda v rozpore s danou podmienkou). Keď však danú stenu kocky zvážime súčasne so stenou s ňou rovnobežnou (t. j. stenou protiľahlou), pri ktorej vrcholoch sú tiež nanajvýš dve \(N\), a zohľadníme pritom, že pri ôsmich vrcholoch týchto dvoch stien (teda pri všetkých ôsmich vrcholoch kocky) sú (všetky) štyri \(N\), dôjdeme 1k záveru, že pri vrcholoch každej steny sú práve dve \(N\) (a teda aj dve \(P\)). Naopak, každé také pripísanie štyroch \(N\) a štyroch \(P\) zrejme vyhovuje požiadavkám úlohy.
Stojíme tak pred úlohou určiť počet tých pripísaní štyroch \(N\) a štyroch \(P\) vrcholom kocky \(ABCDEFGH\), pri ktorých sú dve \(N\) a dve \(P\) pri vrcholoch každej steny. Rozdelíme ich na dve skupiny podľa toho, či existuje stena, na ktorej sú obe \(N\) priradené vrcholom susedným (na kocke tak vznikne aspoň jedna hrana ”\(NN\)“), alebo naopak vo všetkých stenách sú obe \(N\) priradené vrcholom protiľahlým (všetky hrany kocky potom budú ”\(N\)P“). Po jednom reprezentantovi oboch skupín vidíme na obr. 1 – pre lepší prehľad bez označenia vrcholov kocky písmenami. Ľahko overíme (výklad tu vynecháme), že znaky v krúžku pri reprezentantoch oboch skupín už jednoznačne určujú znaky pri všetkých ostatných vrcholoch kocky.
Teraz už ľahko usúdime, že v prvej skupine je práve šesť priradení – jednou hranou ”\(NN\)“ je totiž, ako vieme, celé vyhovujúce priradenie určené a má práve dve hrany ”\(NN\)“, ktoré sú pritom rovnobežné a neležia v jednej stene; takých dvojíc hrán je pre kocku \(ABCDEFGH\) práve šesť. Naproti tomu v druhej skupine sú iba dve rzne priradenia – pretože sa jedná o priradenie bez hrany ”\(NN\)“; znakom \(P\) alebo \(N\) pri vrchole \(A\) danej kocky sú totiž, ako vieme, určené znaky pri všetkých ďalších jej vrcholoch. Existuje tak spolu \(6 + 2 = 8\) vyhovujúcich priradení štyroch \(N\) a štyroch \(P\) vrcholom kocky \(ABCDEFGH\).
V ďalšej, jednoduchšej časti nášho postupu určíme, koľkými spôsobmi môžeme štyri \(N\) a štyri \(P\) (pevne pripísané vrcholom kocky) zameniť konkrétnymi číslami 1, 3, 3, 3, 4, 4, 4, 4. Máme zrejme práve štyri možnosti pre výber toho \(N\), ktoré zameníme číslom 1; potom už zvyšné tri \(N\) musíme zameniť číslom 3, rovnako ako všetky štyri \(P\) číslom 4. Počet spôsobov zámen znakov \(N\) a \(P\) danými číslami je tak rovný 4.
Nakoniec uplatníme jednoduché kombinatorické pravidlo súčinu: keďže existuje osem vyhovujúcich pripísaní znakov \(N\) a \(P\) k vrcholom danej kocky a pri každom z nich možno štyrmi spôsobmi zameniť znaky \(N\) a \(P\) danými číslami, je hľadaný počet vyhovujúcich pripísaní daných čísel vrcholom danej kocky rovný \(8 \cdot 4 = 32\).
Úloha 61-I-6-N2
Riešenie*
Komentár
Úloha je malým opakovaním toho, ktoré čísla do 100 sú prvočísla a môžeme ju využiť na pripomenutie definície prvočísla. Rovnako ako aj v nasledujúcich úlohách, aj tu môžeme študentov nechať najprv odohrať niekoľko hier a potom skúsiť ich čiastkové zistenia spoločne pretaviť do univerzálnej stratégie.Úloha 57-I-3
Riešenie*
Skúška. Majme šesť krabičiek a osem guľôčok. Keď do každej krabičky dáme práve jednu guľôčku, ostane \(n = 2\) guľôčok. Keď však odoberieme dve krabičky, môžeme do zostávajúcich štyroch rozdeliť guľôčky práve po dvoch. Podmienky úlohy sú teda splnené. Pre šesť krabičiek a deväť guľôčok urobíme skúšku rovnako ľahko.
Záver. Buď máme šesť krabičiek a osem guľôčok, alebo šesť krabičiek a deväť guľôčok.
Komentár
Úloha, spolu s úlohou predchádzajúcou, je bežnou slovnou úlohou vedúcou na sústavu rovníc. Jej úspešné vyriešenie však vyžaduje umnú manipuláciu s výrazmi.Úloha 63-I-4-N3
a) Ak majú dva trojuholníky rovnakú výšku, potom pomer ich obsahov sa rovná pomeru dĺžok príslušných základní.
b) Ak majú dva trojuholníky zhodné základne, potom pomer ich obsahov sa rovná pomeru príslušných výšok.
Riešenie
b) Označme zhodnú základňu dvoch trojuholníkov \(z\), v trojuholníku \(T_1\) je výška na túto základňu \(v_1\), v trojuholníku \(T_2\) je výška na túto základňu \(v_2\). Pomer obsahov trojuholníkov \(T_1\) a \(T_2\) je \[\frac{S_{T_1}}{S_{T_2}}=\frac{\frac{1}{2}zv_1}{\frac{1}{2}zv_2}=\frac{v_1}{v_2},\] čo je pomer príslušných výšok.
Úloha B-60-I-1-N4
Riešenie*
Úloha 62-I-4-N3
Riešenie*
Úloha 59-I-6-N4
Riešenie*
Úloha 61-I-4-N8
Riešenie*
Úloha 62-I-2-D1
Riešenie*
Úloha 65-I-3-D2
Riešenie*
Úloha 60-I-4-N2
Riešenie*
Úloha 66-I-4-N1
Riešenie
Úloha 65-I-4-D3
Riešenie*
Úloha 58-S-1
Riešenie*
Komentár
Úloha demonštruje jeden zo základných spôsobov dokazovania nerovností: úpravu výrazu na jednej strane nerovnosti na tvar, o ktorom s určitosťou vieme, že je nezáporný/nekladný a jeho porovnanie s nulou. Taktiež si študenti precvičia ekvivalentné úpravy nerovností a úpravy výrazov do tvaru súčinu.Úloha 61-I-4-N4
Riešenie*
Úloha 59-I-3-D3
Riešenie*
Úloha 60-I-4-D1
a) Dokážte, že ak medzi každými štyrmi osobami sú aspoň štyri dvojice známych, tak každé dve osoby, ktoré sa nepoznajú, majú spoločného známeho.
b) Zistite, pre ktoré \(n \geq 4\) existuje skupina osôb, v ktorej sú medzi každými štyrmi osobami aspoň tri dvojice známych a súčasne sa niektoré dve osoby ani nepoznajú, ani nemajú spoločného známeho.
c) Rozhodnite, či v skupine šiestich osôb môžu byť v každej štvorici práve tri dvojice známych a práve tri dvojice neznámych.
Riešenie*
Úloha 66-II-3
Riešenie*
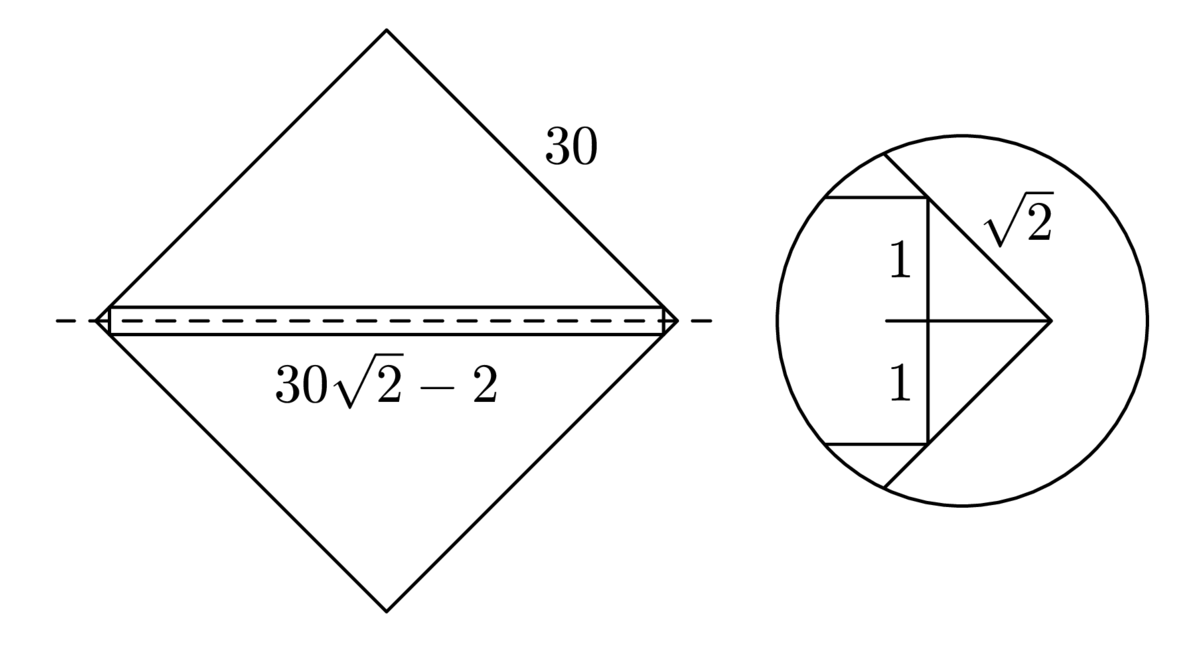
pravouhlého trojuholníka so stranami \(2, \sqrt{2}, \sqrt{2}\), pozri zväčšenú časť obr. 1), takže stačí ukázať, že \(30\sqrt{2}-2\geq 40\). To je ekvivalentné s nerovnosťou \(5\sqrt{2}\geq 7\), čiže \(50 \geq 49\), čo je splnené. Daný obdĺžnik \(32 \times 120\) teda naozaj možno zakryť siedmimi štvorcami so stranou 30.
Úloha 61-S-3
Riešenie
Úloha (Thiele 1986), príklad 3, str. 95
Riešenie*
Komentár
Úloha, v ktorej opäť predtým, než uplatníme znalosti o deliteľnosti, príp. prvočíslach, musíme umne upraviť východiskový tvar rovnice.Thiele, Rüdiger. 1986. Matematické Důkazy. 2. nezměněné vydání. Praha: Státní nakladatelství technické literatury.
Úloha 59-I-5-D2
Riešenie*
Úloha 66-I-2
Riešenie*
| \(n\) | \(V (n)\) |
|---|---|
| 1 | 0 |
| 2 | \(48 = 2^4 \cdot 3\) |
| 3 | \(168 = 2^3 \cdot 3 \cdot 7\) |
| 4 | \(420 = 2^2 \cdot 3 \cdot 5 \cdot 7\) |
Z toho vidíme, že hľadaný deliteľ \(d\) všetkých čísel \(V (n)\) musí byť deliteľom čísla \(2^2 \cdot 3 = 12\), spĺňa teda nerovnosť \(d \leq 12\). Preto ak ukážeme, že číslo \(d = 12\) zadaniu vyhovuje, t. j. že \(V (n)\) je násobkom čísla 12 pre každé prirodzené \(n\), budeme s riešením hotoví.
Úprava \[V (n) = n^4+ 11n^2 - 12 = (12n^2 - 12) + (n^4 - n^2),\] pri ktorej sme z výrazu \(V (n)\) ”vyčlenili“ dvojčlen 1\(2n^2 -12\), ktorý je zrejmým násobkom čísla 12, redukuje našu úlohu na overenie deliteľnosti číslom 12 (teda deliteľnosti číslami 3 a 4) dvojčlena \(n^4 - n^2\) . Využijeme na to jeho rozklad \[n^4 - n^2 = n^2(n^2 - 1) = (n - 1)n^2(n + 1).\] Pre každé celé \(n\) je tak výraz \(n^4 - n^2\) určite deliteľný tromi (také je totiž jedno z troch po sebe idúcich celých čísel \(n - 1\), \(n\), \(n + 1\)) a súčasne aj deliteľný štyrmi (zaručuje to v prípade párneho \(n\) činiteľ \(n^2\), v prípade nepárneho \(n\) dva párne činitele \(n-1\) a \(n+1\)).
Dodajme, že deliteľnosť výrazu \(V (n)\) číslom 12 možno dokázať aj inými spôsobmi, napríklad môžeme využiť rozklad \(V (n) = n^4+ 11n^2 - 12 = (n^2+ 12)(n^2 - 1)\) z predchádzajúcej úlohy alebo prejsť k dvojčlenu \(n^4 + 11n^2\) a podobne.
Záver. Hľadané číslo \(d\) je rovné 12.
Komentár
Úloha je okrem využitia všetkých doterajších poznatkov zaradená aj z dôvodu prvého kroku riešenia. Je vhodné študentom ukázať, že preskúmanie výrazu pre niekoľko malých hodnôt \(n\) nám môže pomôcť utvoriť si predstavu o tom, ako sa bude výraz správať ďalej, príp. vytvoriť hypotézu, ktorú sa neskôr pokúsime dokázať. Táto metóda nájde uplatnenie nielen v tejto konkrétnej úlohe, ale aj v ďalších partiách matematiky.Úloha B-65-I-5-D2
Riešenie*
Úloha 57-I-3-N1
Riešenie
Úloha 65-I-3
Nájdite všetky reálne čísla \(x\) a \(y\), pre ktoré daný výraz nadobúda svoju najmenšiu hodnotu.
Určte všetky dvojice celých nezáporných čísel \(x\) a \(y\), pre ktoré je hodnota daného výrazu rovná číslu 16.
Riešenie*
a) Prvé dva sčítance v poslednom súčte sú druhé mocniny, majú teda nezáporné hodnoty. Minimum určite nastane v prípade, keď pre niektoré \(x\) a \(y\) budú oba základy rovné nule (v tom prípade pre inú dvojicu základov už bude hodnota výrazu \(V (x, y)\) väčšia). Obe rovnosti \(x - y = 0\), \(x + 1 = 0\) súčasne naozaj nastanú, a to zrejme iba pre hodnoty \(x = y = -1\). Dodajme (na to sa zadanie úlohy nepýta), že \(V_{min} = V~(-1, -1)= 3\). Daný výraz tak nadobúda svoju najmenšiu hodnotu iba pre \(x = y = -1\).
b) Podľa úpravy z úvodu riešenia platí \[V (x, y) = 16 \Leftrightarrow (x -y)^2+ (x + 1)^2+ 3 = 16 \Leftrightarrow (x -y)^2+ (x + 1)^2= 13.\] Oba sčítance \((x - y)^2\) a \((x + 1)^2\) sú (pre celé nezáporné čísla \(x\) a \(y\)) z množiny \(\{0, 1, 4, 9, 16,\,\ldots \}\). Jeden preto zrejme musí byť 4 a druhý 9. Vzhľadom na predpoklad \(x \geq 0\) je základ \(x+1\) mocniny \((x+1)^2\) kladný, musí preto byť rovný 2 alebo 3 (a nie \(-2\) či \(-3\)). V prvom prípade, t. j. pre \(x = 1\), potom pre základ mocniny \((x - y)^2\) dostávame podmienku \(1 - y = \pm\), teda \(y = 1 \pm 3\), čiže \(y = 4\) (hodnota \(y = -2\) je zadaním časti b) vylúčená). V druhom prípade, keď \(x = 2\), dostaneme podobne z rovnosti \(x - y = 2 - y = \pm 2\) dve vyhovujúce hodnoty \(y = 0\) a \(y = 4\). Celkovo teda všetky hľadané dvojice \((x, y)\) sú \((1, 4), (2, 0)\) a \((2, 4)\).
Komentár
Záverečná úloha stavia na poznatkoch z predchádzajúcich úloh, avšak vyžaduje dodatočnú analýzu, preto sme ju zvolili ako vyvrcholenie prvého algebraického seminára.Úloha B-57-II-1
Riešenie*
Ak \(b = a\), majú obidve rovnice tvar \(x^2-ax-a = 0\). Práve jedno riešenie existuje práve vtedy, keď diskriminant \(a^2 + 4a\) je nulový. To platí pre \(a = 0\) a pre \(a = -4\). Pretože \(b = a\), má súčet \(a + b\) v prvom prípade hodnotu \(0\) a v druhom prípade hodnotu \(-8\).
Ak \(x = 1\), dostaneme z daných rovníc \(a + b = 1\), teda \(b = 1-a\). Rovnice potom majú tvar \[x^2-ax + a-1 = 0 \ \ \ \ \text{a} \ \ \ \ x^2 + (a-1)x-a = 0.\] Prvá má korene \(1\) a \(a-1\), druhá má korene \(1\) a \(-a\). Práve jedno spoločné riešenie tak dostaneme vždy s výnimkou prípadu, keď \(a-1 = -a\), čiže \(a = \frac{1}{2}\) – vtedy sú spoločné riešenia dve.
Záver. Najmenšia hodnota súčtu \(a + b\) je \(-8\) a je dosiahnutá pre \(a = b = -4\). Najväčšia hodnota súčtu \(a + b\) je \(1\); túto hodnotu má súčet \(a + b\) pre všetky dvojice \((a, 1-a)\), kde \(a\neq \frac{1}{2}\) je ľubovoľné reálne číslo.
Komentár
Úloha nadväzuje na predchádzajúcu, opäť rovnice v zadaní sčítame. Viac ako náročnosťou výpočtu je úloha zaujímavá svojim rozborom, kde je potrebné dať pozor na to, aby študenti správne zvážili oba prípady (\(a=b\), \(x=1\)).Úloha 62-I-4-N2
Riešenie*
Úloha 66-I-4-N2
Riešenie
Komentár
Predchádzajúce dve jednoduchšie úlohy majú prípravný charakter na nasledujúcu úlohu a domácu prácu. Študenti si prostredníctvom nich zopakujú metódy riešenia sústav rovníc s viacerými neznámymi. Tieto metódy by študentom mali byť známe zo ZŠ, ak však zistíme, že ich používanie nie je až také samozrejmé, je vhodné zaradiť niekoľko jednoduchších úloh, napr. z (Kubát, Hrubý, and Pilgr 2000).Kubát, Josef, Dag Hrubý, and Josef Pilgr. 2000. Sbírka úloh Z Matematiky Pro Střední školy: Maturitní Minimum. 1. vydání. Praha: Prometheus.
Úloha 61-I-3-N3
Riešenie*
Úloha 61-I-4-N1
Riešenie*
Úloha 57-I-4-D3
Riešenie*
Úloha 60-I-1
Riešenie*
Komentár
Ak sa študenti rozhodnú riešiť sústavy rovníc pre spomínané štyri prípady, je to v poriadku, na záver by však bolo inšpiratívne ukázať im aj rýchlejší postup.Úloha
Riešenie

Keďže uhly \(ABD\) a \(BDC\) sú striedavé, majú rovnakú veľkosť. Podobne uhly \(BAC\) a \(ACD\) sú rovnako veľké, pretože sú takisto dvojicou striedavých uhlov. Potom sú trojuholníky \(ABU\) a \(CDU\) zhodné, keďže sa zhodujú v jednej strane \(|AB|=|CD|\) a v dvoch k nej priľahlých uhloch. Preto aj \(|AU|=|UC|\), \(|BU|=|UD|\) a tvrdenie je dokázané.
Úloha B-63-S-3
Riešenie

[fig:B63S3_1]
zvyčajným spôsobom \(a\), \(b\), \(c\) dĺžky jednotlivých strán, platí \[a = y + z, \ \ \ \ b = z + x, \ \ \ \ c = x + y.\] Sčítaním týchto troch rovníc dostaneme (pomocou \(s\) ako zvyčajne označujeme polovičný obvod trojuholníka) \[2s = a + b + c = 2x + 2y + 2z,\] takže nám vyjde \[\label{eq:B63S3} x + y + z = s, \ \ \ \ x = s - a,\ \ \ \ y = s - b, \ \ \ \ z = s - c.\] Pozrime sa teraz na pripísanú kružnicu trojuholníku \(ABC\), ktorá sa dotýka jeho strany \(BC\) v bode \(P\) a polpriamok \(AB\) a \(AC\) v bodoch \(R\) a \(Q\) (obr. [fig:B63S3_2]). Zo zhodnosti úsekov príslušných dotyčníc k tejto kružnici máme \[|AR| = |AQ|, \ \ \ \ |BR| = |BP|, \ \ \ \ |CP| = |CQ|,\] odkiaľ vychádza \[\begin{aligned} 2|AR| = |AR| + |AQ| & = |AB| + |BR| + |AC| + |CQ| = \\ & = |AB| + |BP| + |AC| + |CP| = a + b + c = 2s,\end{aligned}\] čiže \(|AR| = |AQ| = s\). Z tejto rovnosti ale vyplýva, že \(|BP| = |BR| = s - c\), čo je podľa [eq:B63S3] zároveň dĺžka z úsečky \(CX\), teda \(|BP| = |CX|\). To znamená, že body \(P\) a \(X\) sú súmerne združené podľa stredu úsečky \(BC\).

[fig:B63S3_2]
Analogicky by sme odvodili rovnosti \(|BK| = s\) a \(|CL| = s\) pre body dotyku \(K\) a \(L\) kružníc pripísaných stranám \(CA\) a \(AB\) (obr. [fig:B63S3_2]) trojuholníka \(ABC\) s priamkou \(a\). Z týchto posledných rovností však vidíme, že \(|BL| = s - a = |CK|\), teda aj body \(K\) a \(L\) sú súmerne združené podľa stredu úsečky \(BC\). Body \(K\) a \(L\) sú známe (z troch daných bodov na priamke sú to tie dva krajné), poznáme teda aj stred \(S\) strany \(BC\) (je to stred úsečky \(KL\)) a bod \(X\) nájdeme ako obraz tretieho daného bodu \(P\) v stredovej súmernosti podľa stredu úsečky \(BC\).
Úloha 62-I-2-D5
Riešenie*
Úloha 65-I-4-N2
Riešenie*
Úloha 63-S-3
Riešenie*
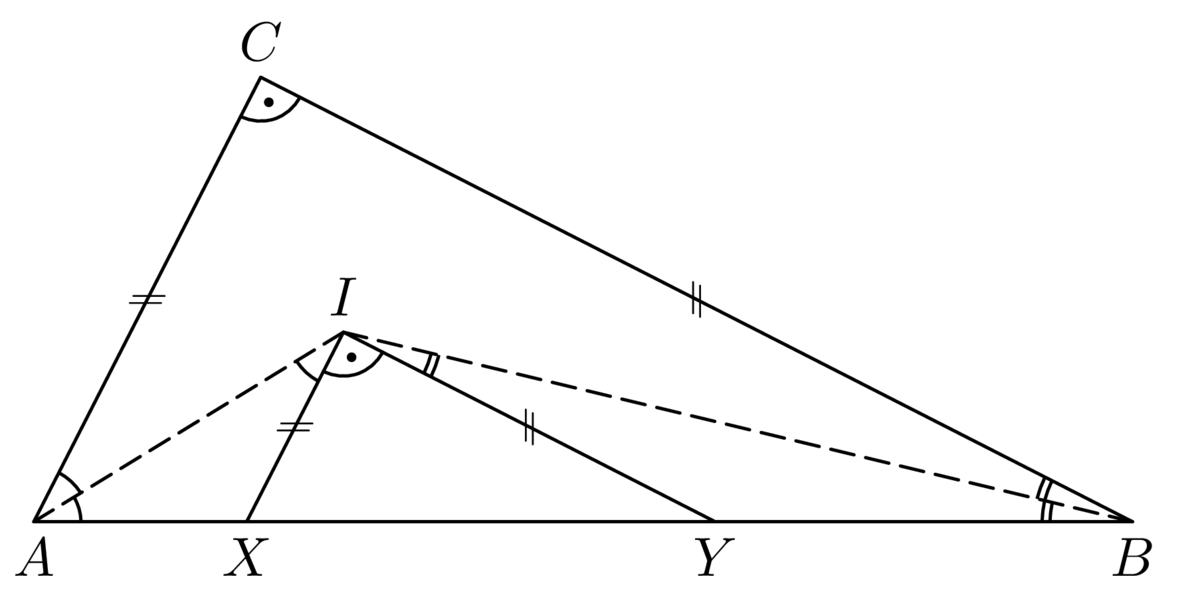
Komentár
Úloha už vyžaduje trochu viac invencie a postrehu, keďže kľúčovým krokom v riešení je všimnúť si, že trojuholníky \(AIX\) a \(BIY\) sú rovnoramenné. K tomu však študentov môže naviesť poloha bodu \(I\), ktorý leží na osi uhlov a to, že rovnobežky \(AC\) a \(XI\), resp. \(BC\) a \(YI\) sú preťaté priečkami \(AI\), resp. \(BI\), takže v náčrtku vieme nájsť niekoľko dvojíc zhodných uhlov. Úloha tak kombinuje použitie Pytagorovej vety aj vlastnosti rovnoramenných trojuholníkov.Úloha 66-I-3
Riešenie*

[fig:66I3_1]
Pytagorova veta pre pravouhlé trojuholníky \(ACD\) a \(BCD\) vedie k dvojakému vyjadreniu druhej mocniny spoločnej odvesny \(CD\), pričom v situácii naľavo dostaneme \[|CD|^2= b^2- \bigg(\frac{2}{3}c\bigg)^2= a^2 - \bigg(\frac{1}{3}c\bigg)^2,\] odkiaľ po jednoduchej úprave poslednej rovnosti dostaneme vzťah \[3(b^2 - a^2) = c^2.\] Pre druhú situáciu vychádza analogicky \[3(a^2 -b^2) = c^2.\] Závery pre obe možnosti možno zapísať jednotne ako rovnosť s absolútnou hodnotou \[3|a^2 - b^2 | = c^2.\] Ak použijeme rozklad \(|a^2 - b^2 | = |a - b|(a + b)\) a nerovnosť \(c < a + b\) (ktorú ako je známe spĺňajú dĺžky strán každého trojuholníka \(ABC\)), dostaneme z odvodenej rovnosti \[3|a - b|c < 3|a - b|(a + b) = c^2,\] odkiaľ po vydelení kladnou hodnotou \(c\) dostaneme \(3|a - b| < c\), ako sme mali dokázať. Zdôraznime, že nerovnosť \(3|a-b|c < 3|a-b|(a+b)\) sme správne zapísali ako ostrú – v prípade \(a = b\) by síce prešla na rovnosť, avšak podľa nášho odvodenia by potom platilo \(c^2 = 0\), čo odporuje tomu, že ide o dĺžku strany trojuholníka.
Iné riešenie*. Nerovnosť, ktorú máme dokázať, možno po vydelení tromi zapísať bez absolútnej hodnoty ako dvojicu nerovností \[-\frac{1}{3}c < a - b < \frac{1}{3}c.\] Opäť ako v pôvodnom riešení rozlíšime dve možnosti pre polohu päty \(D\) uvažovanej výšky a ukážeme, že vypísanú dvojicu nerovností možno upresniť na tvar \[-\frac{1}{3} < a - b < 0,\ \ \ \ \text{respektíve} \ \ \ \ 0 < a - b <\frac{1}{3}c,\] podľa toho, či nastáva situácia z ľavej či pravej časti obr. [fig:66I3_1].
Pre situáciu z obr. [fig:66I3_1] naľavo prepíšeme avizované nerovnosti \(-\frac{1}{3}c < a - b < 0\) ako \(a < b < a +\frac{1}{3}c\) a odvodíme ich z pomocného trojuholníka \(ACE\), pričom \(E\) je stred úsečky \(AD\), takže body \(D\) a \(E\) delia stranu \(AB\) na tri zhodné úseky dĺžky \(\frac{1}{3}c\).

[fig:66I3_2]
V obr. [fig:66I3_2] sme rovno vyznačili, že úsečka \(EC\) má dĺžku \(a\) ako úsečka \(BC\), a to v dôsledku zhodnosti trojuholníkov \(BCD\) a \(ECD\) podľa vety \(sus\). Preto je pravá z nerovností \(a < b < a +\frac{1}{3}c\) porovnaním dĺžok strán trojuholníka \(ACE\), ktoré má všeobecnú platnosť.
Ľavú nerovnosť \(a < b\) odvodíme z druhého všeobecného poznatku, že totiž v každom trojuholníku oproti väčšiemu vnútornému uhlu leží dlhšia strana. Stačí nám teda zdôvodniť, prečo pre uhly vyznačené na obr. [fig:66I3_2] platí \(|\measuredangle CAE| < |\measuredangle AEC|\). To je však jednoduché: zatiaľ čo uhol \(CAE\) je vďaka pravouhlému trojuholníku \(ACD\) ostrý, uhol \(AEC\) je naopak tupý, pretože k nemu vedľajší uhol \(CED\) je ostrý vďaka pravouhlému trojuholníku \(CED\).
Pre prípad situácie z obr. [fig:66I3_1] napravo možno predchádzajúci postup zopakovať s novým bodom \(E\), tentoraz stredom úsečky \(BD\). Môžeme však vďaka súmernosti podľa osi \(AB\) konštatovať, že z dokázaných nerovností \(-\frac{1}{3}c < a - b < 0\) pre situáciu naľavo vyplývajú nerovnosti \(-\frac{1}{3}c < b - a < 0\) pre situáciu napravo, z ktorých po vynásobení číslom \(-1\) dostaneme práve nerovnosti \(0 < a - b <\frac{1}{3}\), ktoré sme mali v druhej situácii dokázať.
Komentár
Nosným prvkom úlohy je opäť Pytagorova veta, väčšiu pozornosť však vyžaduje rozbor úlohy, keďže päta výšky sa môže nachádzať v dvoch rôznych polohách.Úloha B-65-II-2
Riešenie*

[fig:B65II2_1]
na polomer \(BF\) kružnice \(m\), a preto sa priamka \(AF\) dotýka kružnice \(m\) v bode \(F\) (obr. [fig:B65II2_1]). Z rovnosti úsekového uhla zovretého tetivou \(DF\) s dotyčnicou \(AF\) a obvodového uhla nad tou istou tetivou máme (ako už je vyznačené na obrázku) \[|\measuredangle AFD| = |\measuredangle DEF|.\] Zo súmernosti úsečky \(EF\) podľa osi \(AB\) tak vyplýva \[|\measuredangle AFD| = |\measuredangle DEF| = |\measuredangle DFE|,\] čo znamená, že \(FD\) je osou uhla \(AFE\).
Iné riešenie*. Označme \(\beta\) veľkosť uhla \(ABF\) a dopočítajme veľkosti uhlov \(DFE\) a \(AFE\). Trojuholník \(DBF\) je rovnoramenný, lebo jeho ramená \(BD\) a \(BF\) sú polomery kružnice \(m\), preto \[|\measuredangle DFB| = \frac{1}{2}(180^\circ-\beta) = 90^\circ-\frac{\beta}{2}.\] Keďže podobne aj trojuholník \(EBF\) je rovnoramenný s osou \(BD\), platí \[|\measuredangle EFB| = 90^\circ-\beta.\] Spojením oboch predchádzajúcich rovností tak dostávame \[|\measuredangle DFE| = |\measuredangle DFB| - |\measuredangle EFB| =\frac{\beta}{2}.\] Z vlastností Tálesovej kružnice \(k\) nad priemerom \(AB\) vieme, že uhol \(AFB\) je pravý. Pritom jeho časť uhol \(EFB\) má, ako sme už zistili, veľkosť \(90^\circ-\beta\), takže jeho druhá časť, uhol \(AFE\), má veľkosť \(\beta\), čo je presne dvojnásobok veľkosti uhla \(DFE\). Tým sme dokázali, že priamka \(FD\) je osou uhla \(AFE\).
Iné riešenie*. Nad oblúkom \(AE\) kružnice \(k\) sa zhodujú uhly \(ABE\) a \(AFE\) (obr. [fig:B65II2_2]). Oblúku \(DE\) kružnice \(m\) prislúcha obvodový uhol \(DFE\) a stredový uhol \(DBE\). Spolu tak dostávame \[|\measuredangle DFE| = \frac{1}{2} |\measuredangle DBE| = \frac{1}{2} |\measuredangle ABE| = \frac{1}{2} |\measuredangle AFE|,\] čo dokazuje, že \(FD\) je osou uhla \(AFE\).

[fig:B65II2_2]
Komentár
Úlohu je možné riešiť viacerými rôznymi spôsobmi, preto je to opäť vhodný priestor na to, aby ši študenti svoje riešenia porovnali a skúsili obhájiť pred spolužiakmi. V úlohe sa znova vyskytla spoločná tetiva dvoch kružníc, pekne tak nadväzuje na úlohu predchádzajúcu.Úloha 64-I-6-N3
Riešenie*
Úloha 61-S-1
Riešenie*
V prípade \(a = 2\) (vzhľadom na to, že \(b\) je nepárne) platí \[a \cdot [a, b] = 2 \cdot [2, b] = 2 \cdot 2b = 4b,\] čo znamená, že prvá rovnosť v [eq:61S1] je splnená jedine pre \(b = 45\). Vtedy \(b \cdot (a, b) = 45 \cdot (2, 45) = 45\), takže je splnená aj druhá rovnosť v [eq:61S1], a preto dvojica \(a = 2, b = 45\) je riešením úlohy.
V prípade \(a = 6\) podobne dostaneme \[a \cdot [a, b] = 6 \cdot [6, b] = 6 \cdot 2 \cdot [3, b] = 12 \cdot [3, b],\] čo znamená, že prvá rovnosť v [eq:61S1] je splnená práve vtedy, keď \([3, b] = 15\). Tomu vyhovujú jedine hodnoty \(b = 5\) a \(b = 15\). Z nich však iba hodnota \(b = 15\) spĺňa druhú rovnosť v [eq:61S1], ktorá je teraz v tvare \(b\cdot(6, b) = 45\). Druhým riešením úlohy je teda dvojica \(a = 6\), \(b = 15\), žiadne ďalšie riešenia neexistujú.
Záver. Hľadané dvojice sú dve, a to \(a = 2, b = 45\) a \(a = 6, b = 15\).
Iné riešenie*. Označme \(d = (a, b)\). Potom \(a = ud\) a \(b = vd\), pričom \(u, v\) sú nesúdeliteľné prirodzené čísla, takže \([a, b] = uvd\). Z rovností \[a \cdot [a, b] = ud \cdot uvd = u^2vd^2 \ \ \ \text{a} \ \ \ \ b \cdot (a, b) = vd \cdot d = vd^2\] vidíme, že číslo \(a \cdot [a, b]\) je \(u^2\)-násobkom čísla \(b \cdot (a, b)\), takže zadaná rovnosť množín môže byť splnená jedine tak, ako sme zapísali vzťahmi (1) v prvom riešení. Tie teraz môžeme vyjadriť rovnosťami \[u^2vd^2= 180 \ \ \ \text{a} \ \ \ \ vd^2= 45.\] Preto platí \(u^2 =180/45= 4\), čiže \(u = 2\). Z rovnosti \(vd^2 = 45 = 3^2 \cdot 5\) vyplýva, že buď \(d = 1\) (a \(v = 45\)), alebo \(d = 3\) (a \(v = 5\)). V prvom prípade \(a = ud = 2 \cdot 1 = 2\) a \(b = vd = 45 \cdot 1 = 45\), v druhom \(a = ud = 2 \cdot 3 = 6\) a \(b = vd = 5 \cdot 3 = 15\).
Poznámka. Keďže zo zadanej rovnosti okamžite vyplýva, že obe čísla \(a, b\) sú deliteľmi čísla 180 (takým deliteľom je dokonca aj ich najmenší spoločný násobok \([a, b]\)), je možné úlohu vyriešiť rôznymi inými cestami, založenými na testovaní konečného počtu dvojíc konkrétnych čísel \(a\) a \(b\). Takýto postup urýchlime, keď vopred zistíme niektoré nutné podmienky, ktoré musia čísla \(a, b\) spĺňať. Napríklad spresnenie rovnosti množín na dvojicu rovností (1) možno (aj bez použitia úvahy o parite čísel \(a, b\)) vysvetliť všeobecným postrehom: súčin \(a \cdot [a, b]\) je vždy deliteľný súčinom \(b \cdot (a, b)\), pretože ich podiel možno zapísať v tvare \[\frac{a \cdot [a, b]}{b \cdot (a, b)}=\frac{a}{(a, b)}\cdot\frac{[a, b]}{b},\] teda ako súčin dvoch celých čísel.
Komentár
Úloha je zložitejšia ako predchádzajúce, dá sa však riešiť mnohými spôsobmi a bude iste zaujímavé vidieť rôzne študentské riešenia. Je taktiež vhodným miestom na to, aby sme študentov nechali diskutovať o prístupoch medzi sebou a prípadne skúšali hľadať slabiny jednotlivých zdôvodnení. Určite považujeme za vhodné zmieniť poslednú rovnosť z poznámky, keďže ide o zaujímavý postreh a metóda vhodného zapísania tvaru zlomku je užitočná nielen tu. Na túto úlohu nadväzuje komplexnejšia domáca práca, ktorá však vychádza z veľmi podobného princípu.Úloha 57-I-3-N2
Riešenie*
Úloha 66-I-2-N1
Riešenie
Komentár
Táto jednoduchá úloha zoznámi žiakov s poznatkom často využívaným v úlohách zameraných na dokazovanie deliteľnosti číslom, ktoré je násobkom troch: z troch po sebe idúcich prirodzených čísel je vždy práve jedno deliteľné tromi.Úloha 61-I-3-N1
Riešenie*
Komentár
Úloha je relatívne jednoduchá a nevyžaduje žiadne špeciálne znalosti, zároveň však nie je triviálna. Tvorí tak príjemné preklenutie medzi školskými a olympiádnymi príkladmi.Úloha B-58-I-5-D1
Riešenie*
Úloha 60-I-3-N1
Vypočítajte obsah trojuholníka \(ADP\).
Vypočítajte obsah lichobežníka \(ABCD\).
Riešenie*
Úloha 61-I-3-N2
Riešenie*
Úloha 62-I-2-N1
Riešenie*
Komentár
Vyššie dokázaná nerovnosť je špeciálnym prípadom tzv. AG-nerovnosti medzi aritmetickým a geometrickým priemerom ľubovoľných nezáporných čísel. Jej všeobecnejší tvar pre viac ako dve čísla však v tomto momente nepovažujeme za dôležité so študentami pokrývať, keďže AG-nerovnosť sa v úlohách kategórie C vyskytla v posledných rokoch veľmi zriedka (a aj vtedy bolo nerovnosti možné dokázať inými metódami). Je to však veľmi užitočný nástroj, ktorému by sme sa venovali v pokračovaní seminára vo vyšších ročníkoch.Jeho využitie budeme demonštrovať v nasledujúcej úlohe.
Úloha 60-I-2-N1
Riešenie*
Úloha 59-I-3
Riešenie*
Iné riešenie*. Rovnicu upravíme na tvar \(2x - \frac{5}{2} = \lfloor x\rfloor\). Taká rovnica bude splnená práve vtedy, keď číslo \(2x - \frac{5}{2}\) bude celé a bude spĺňať nerovnosti \(x - 1 < 2x - \frac{5}{2} \leq x\), ktoré sú ekvivalentné s podmienkou \(\frac{3}{2} < x \leq \frac{5}{2}\). Pre takéto \(x\) zrejme hodnoty výrazu \(2x - \frac{5}{2}\) vyplnia interval \(( \frac{1}{2}, \frac{5}{2} \rangle\). V ňom ležia práve dve celé čísla 1 a 2, teda hľadané \(x\) nájdeme z rovníc \(2x - \frac{5}{2} = 1\) a \(2x - \frac{5}{2} = 2\).
Komentár
Aj napriek tomu, že funkcia dolná celá časť nie je bežným učivom preberaným v školách, nemala by analýza úlohy robiť žiakom veľké problémy.Úloha 64-I-2
Riešenie*
Ak sa otočí 15-minútová ručička o uhol \(\alpha\), otočí sa 3-minútová ručička o uhol \(5\alpha\) a minútová ručička o uhol \(15\alpha\). Keďže každé dve ručičky v hľadaných polohách spolu zvierajú uhol \(120^{\circ}\) a 3-minútová ručička je rýchlejšia ako 15-minútová, dajú sa hľadané polohy získať ako riešenia rovnice \(5\alpha-\alpha = k \cdot 120^{\circ}\), ktorými sú uhly \(\alpha = k \cdot 30^{\circ}\), pričom \(k\) nadobúda kladné celé hodnoty, ktoré nie sú násobkami troch, inak by sa dotyčné ručičky prekrývali.
Môžeme teda postupovať tak, že budeme testovať hodnoty \(\alpha = k\cdot 30^{\circ}\) postupne pre jednotlivé hodnoty čísla \(k\). Naozaj tak začneme a priebežne uvidíme, ako sa dajú po niekoľkých krokoch vďaka periodickosti získať všetky ďalšie riešenia danej úlohy.
Uvažujme najskôr \(k = 1\), teda \(\alpha = 30^{\circ}\). Pri tejto hodnote sa otočila najrýchlejšia ručička o uhol \(450^{\circ}\). V tomto okamihu sa najpomalšia ručička nachádza na čísle 1 ciferníka, druhá ručička na čísle 5 a najrýchlejšia ručička na čísle 3. Tento prípad teda nie je riešením danej úlohy.
Nech je ďalej \(k = 2\), čiže \(\alpha = 60^{\circ}\). Pri tejto hodnote sa otočila najrýchlejšia ručička o uhol \(900^{\circ}\). V tomto okamihu sa najpomalšia ručička nachádza na čísle 2 ciferníka, druhá ručička na čísle 10 a najrýchlejšia ručička na čísle 6. Tento prípad je teda jedným riešením danej úlohy.
Vidíme, že môžeme zostaviť tabuľku, z ktorej jednoducho vyčítame všetky riešenia:
| 15-minútová | 3-minútová | minútová | je riešením? | čas | |
| \(k=1\) | 1 | 5 | 3 | nie | 1,25 min |
| \(k=2\) | 2 | 10 | 6 | áno | \(2\cdot 1,25\) min |
| \(k=4\) | 4 | 8 | 12 | áno | \(4\cdot 1,25\) min |
| \(k=5\) | 5 | 1 | 3 | nie | |
| \(k=7\) | 7 | 11 | 9 | nie | |
| \(k=8\) | 8 | 4 | 12 | áno | \(8\cdot 1,25\) min |
| \(k=10\) | 10 | 2 | 6 | áno | \(10\cdot 1,25\) min |
| \(k=11\) | 11 | 7 | 9 | nie | |
| \(k=12\) | 12 | 12 | 12 | nie |
Do tabuľky sme uviedli aj ”zakázanú“ hodnotu \(k = 12\) deliteľnú tromi, pri ktorej sa všetky tri ručičky prekryjú, takže v ďalšom priebehu sa budú ich polohy periodicky opakovať. Časy, v ktorých to nastane, budú vždy o 15 minút dlhšie. Zistili sme tak, že všetky hľadané časy sú
\[\begin{aligned} t &= (12n + 2) \cdot 1, 25\,\text{min} =(15n + 2, 5)\,\text{min},\\ t &= (12n + 4) \cdot 1, 25\,\text{min}= (15n + 5)\,\text{min},\\ t &= (12n + 8) \cdot 1, 25\,\text{min} = (15n + 10)\,\text{min},\\ t &= (12n + 10) \cdot 1, 25 \,\text{min} = (15n + 12, 5)\,\text{min},\end{aligned}\]
pričom \(n = 0, 1, 2,\,\ldots\)
Úloha 60-I-1-D1
Riešenie*
Úloha 61-I-4-N7
Riešenie*
Úloha 60-I-5-N3
Riešenie*
Úloha 60-I-1-N1
Riešenie
Úloha 57.I-1-D1
Riešenie*
Úloha B-62-II-1
Riešenie*
Nech naopak pre reálne čísla \(p\), \(q\) a \(k \neq -1\) platí \(kp^2 = (k+1)^2q\). Uvažujme dvojicu reálnych čísel \[x_1 =\frac{-kp}{k + 1} \ \ \ \ \text{a} \ \ \ \ x_2 =\frac{-p}{k + 1}.\] Také čísla (pre ktoré platí \(x_1 = kx_2\)) sú koreňmi danej kvadratickej rovnice, ak spĺňajú obe rovnosti [eq:B62II1]. Overenie urobíme dosadením: \[\begin{aligned}
x_1 + x_2 &= \frac{-kp}{k + 1}+\frac{-p}{k + 1}=\frac{-(k + 1)p}{k + 1}= -p,\\
x_1 x_2 &=\frac{-kp}{k + 1}\cdot\frac{-p}{k + 1}=\frac{kp^2}{(k + 1)^2}=\frac{(k + 1)^2q}{(k + 1)^2}= q.\end{aligned}\] Tým je celý dôkaz hotový.
Úloha 64-I-6-N5
Riešenie*
Úloha 57-I-6-D1
Riešenie*
Úloha 58-II-3
a) Dokážte, že medzi vybranými číslami sú najviac štyri deliteľné tromi. b) Ukážte, že vybraných čísel môže byť 26.
Riešenie*
\[\begin{aligned} T_0 &= \{9, 18, 27,\,\ldots , 99\},\\ T_1 &= \{1, 10, 19,\,\ldots, 91\},\\ T_2 &= \{2, 11, 20,\,\ldots , 92\},\\ \vdots\\ T_8 &= \{8, 17, 26,\,\ldots , 98\}.\end{aligned}\]
a) Našou úlohou je dokázať, že v \(T_0\cup T_3 \cup T_6\) ležia najviac štyri vybrané čísla. Z každej z tried \(T_0, T_3, T_6\) môžu pochádzať najviac dve z vybraných čísel (súčet ľubovoľných troch čísel z jednej takej triedy už totiž deliteľný deviatimi je). Keďže súčet ľubovoľných troch čísel, ktoré po jednom ležia v triedach \(T_0, T_3 a T_6\), je deviatimi deliteľný, aspoň jedna z týchto tried žiadne vybrané číslo neobsahuje. Z oboch vyslovených záverov vyplýva dokazované tvrdenie: vybraných čísel deliteľných tromi je totiž najviac \(2 + 2 + 0 = 4\).
b) Ukážeme, že vyhovujúci výber môže obsahovať 26 čísel. Vyberieme po dvoch číslach z \(T_0, T_3\) a po 11 číslach (teda všetky čísla) z \(T_1\) a \(T_2\). Dostaneme tak celkom \(2 \cdot 2 + 2 \cdot 11 = 26\) čísel; pritom súčet ľubovoľných troch z nich dáva po delení deviatimi zvyšok aspoň \(0 + 0 + 1 = 1\), najviac však \(2 + 3 + 3 = 8\), takže deviatimi deliteľný byť nemôže.
Úloha 61-I-2-N2
\(A\), \(C\), \(V\),
\(A\), \(U\), \(R\),
\(A\), \(P\), \(Q\),
\(A\), \(B\), \(R\).
Riešenie*
Úloha 63-I-4-N4
Riešenie*
Úloha 62-I-2-N1
Riešenie*
Podobným obratom alebo priamym použitím uvedenej AG-nerovnosti (v niektorých prípadoch aj niekoľkonásobným) dokážte ďalšie nerovnosti \[2abc \leq a^2+ b^2c^2 \ , \ a^4+ b^4 \geq a^3b + ab^3 \, \ (1 + a + b)^2 \geq 3(a + b + ab),\] \[\frac{a}{b^2}+\frac{b}{a^2}\geq \frac{1}{a}+\frac{1}{b}\ , \ \frac{1}{ab}+\frac{1}{cd} \geq \frac{8}{(a+b)(c+d)}\ , \ \bigg(a+\frac{1}{b} \bigg) \bigg( b+\frac{1}{c} \bigg) \bigg( c+\frac{1}{a}\bigg) \geq 8,\] v ktorých \(a, b, c, d\) označujú ľubovoľné kladné čísla.
Úloha 64-I-5-N4
Riešenie
Komentár
Všeobecnejší pohľad na predchádzajúci problém by sme dostali skrz pohľad na exponenty prvočísel, z ktorých sú čísla \(a, b, c\) zložené. Skúmaná rovnosť nastane len v prípade, že sú všetky tri čísla navzájom po dvoch nesúdeliteľné.Zároveň úloha demonštruje riešenie uvedením protipríkladu, čo je princíp, s ktorým sme sa v seminároch zatiaľ nestretli a jeho spomenutie je určite vhodné.
Úloha (Herman, Kučera, and Šimša 2011), príklad 2.3, str. 174
Riešenie*
Komentár
Úloha, ktorá vyžaduje viac uvažovania, než tvrdého počítania, je zaujímavá práve jediným výsledkom.Herman, Jiří, Radan Kučera, and Jaromír Šimša. 2011. Metody řešení Matematických úloh I. Brno: MUNI Press.
Úloha 57-I-6-D2, resp. 53-II-4
Riešenie*
V druhej časti riešenia sme mohli postupovať aj nasledovne. Pre číslo \(V = (167 + y) \cdot 13\) vychádzajú z nerovností \(10 \leq y \leq 99\) odhady \(2301 \leq V~\leq 3 458\). Zistíme preto, ktoré z čísel \(\overline{2bb2}\), kde \(b \in \{3, 4, 5, 6, 7, 8, 9\}\) a čísel \(\overline{3bb3}\), kde \(b \in \{0, 1, 2, 3, 4\}\), sú deliteľné trinástimi. Aj keď sa týchto dvanásť čísel dá rýchlo otestovať, urobme to všeobecne ich čiastočným vydelením trinástimi:
\[\begin{aligned} \overline{2bb2} &= 2 002 + 110b = 13 \cdot (154 + 8b) + 6b,\\ \overline{3bb3} &= 3 003 + 110b = 13 \cdot (231 + 8b) + 6b.\end{aligned}\]
Vidíme, že vyhovuje jedine číslo \(\overline{3bb3}\) pre \(b = 0\). Vtedy \(167 + y = 231\), takže \(y = 64\).
Záver. Žiaci mali počítať príklad \(167 + 64 \cdot 13\), teda \(x = 167\), \(y = 64\) a \(z = 13\).
Komentár
Na prvý pohľad sa môže zdať, že úloha nepatrí do tohto seminára, ako sa však v priebehu riešenia ukáže, má tu svoje miesto. Taktiež zaujímavým spôsobom spája poznatky o deliteľnosti, príp. sa v jej riešení uplatnia odhady – túto metódu sme už taktiež v dnešnom seminári využili.Úloha B-58-I-2-N1
Riešenie*
Úloha 59-I-1-N4
Riešenie*
Úloha 65-I-3-D1, resp. B-61-S-1
Riešenie*
Uvažujme preto nasledujúce rozklady: \[18 = 1 + 17 = 3 + 15 = 5 + 13 = 7 + 11 = 9 + 9.\] Medzi uvedenými súčtami je iba jeden (18 = 9 + 9) súčtom druhých mocnín dvoch celých čísel. Môžu teda nastať nasledujúce štyri prípady: \[\begin{aligned}
2x + 1 &= 3, & 2y + 1 &= 3, & \text{ t. j.}\ \ x &= 1, y = 1,\\
2x + 1 &= 3, & 2y + 1 &= -3, & \text{ t. j.} \ \ x &= 1, y = -2,\\
2x + 1 &= -3, & 2y + 1 &= 3, & \text{ t. j.} \ \ x &= -2, y = 1,\\
2x + 1 &= -3, & 2y + 1 &=-3, & \text{ t. j.} \ \ x &= -2, y = -2.\\\end{aligned}\] Záver. Danej rovnici vyhovujú práve štyri dvojice celých čísel \((x, y)\), a to \((1, 1)\), \((1, -2)\), \((-2, 1)\) a \((-2, -2)\).
Iné riešenie*. Danú rovnicu možno upraviť na tvar \(x(x + 1) + y(y + 1) = 4\), z ktorého vidno, že číslo 4 je nutné rozložiť na súčet dvoch celých čísel, z ktorých každé je súčinom dvoch po sebe idúcich celých čísel. Keďže najmenšie hodnoty výrazu \(t(t+ 1)\) pre kladné aj záporné celé \(t\) sú 0, 2, 6, 12, …, do úvahy prichádza iba rozklad \(4 = 2 + 2\), takže každá z neznámych \(x, y\) sa rovná jednému z čísel 1 či \(-2\) – jediných celých čísel \(t\), pre ktoré \(t(t+ 1) = 2\). Navyše je jasné, že naopak každá zo štyroch dvojíc \((x, y)\) zostavených z čísel \(1, -2\) je riešením danej úlohy.
Úloha 59-I-1-N2
Riešenie*
Úloha 63-I-5-N3+63-I-5-N4, resp. 55-I-1
Dokážte, že pre všetky celé kladné čísla \(m\) je rozdiel \(m^6 - m^2\) deliteľný šesťdesiatimi.
Určte všetky kladné celé čísla \(m\), pre ktoré je rozdiel \(m^6 - m^2\) deliteľný číslom 120.
Riešenie*
b) Už sme ukázali, že v prípade nepárneho \(m\) je súčin \((m^2-1)(m^2 + 1)\) deliteľný ôsmimi a číslo \(n = m^6- m^2\) je teda deliteľné číslom \(120 = 8 \cdot 3 \cdot 5\). Ak je však číslo \(m\) párne, sú čísla \(m^2 -1\), \(m^2 + 1\) nepárne, žiadne nie je deliteľné dvoma. Číslo \(n\) je potom deliteľné ôsmimi iba v prípade, že \(m^2\) je deliteľné ôsmimi, teda \(m\) je deliteľné štyrmi. Číslo \(n\) je potom deliteľné šestnástimi, tromi a piatimi, a preto dokonca číslom 240.
Záver. Naše výsledky môžeme zhrnúť. Číslo \(n = m^6 - m^2\) je deliteľné číslom 120 práve vtedy, keď \(m\) je nepárne alebo deliteľné štyrmi.
Komentár
Sada dvoch na seba nadväzujúcich úloh využíva poznatky získané pri riešení jednoduchších prípravných úloh zo začiatku seminára a vyžaduje sústredené a starostlivé aplikovanie všetkých z nich.Úloha 63-I-3-N1
Riešenie*
Úloha 57-I-4-D2
Riešenie*
Úloha B-60-I-1
Riešenie*
Ak \(x = y = z\), prejde pôvodná sústava na jedinú rovnicu \(\sqrt{2x^2} = x + 1\), ktorá má dve riešenia \(x_{1,2} = 1 \pm \sqrt{2}\). Každá z trojíc \((1 \pm \sqrt{2}, 1 \pm \sqrt{2}, 1 \pm{2})\) je zrejme riešením pôvodnej sústavy.
Ak sú niektoré dve z čísel \(x, y, z\) rôzne, napríklad \(x \neq z\), vyplýva z [eq:B60I1] rovnosť \(x+z = - 1\). Dosadením \(x+1 = - z\) do druhej rovnice sústavy dostávame \(y = 0\) a potom z tretej rovnice máme \(x^2 + (x + 1)^2 = 1\), čiže \(x(x + 1) = 0\). Posledná rovnica má dve riešenia \(x = 0\) a \(x = - 1\), ktorým zodpovedajú \(z = - 1\) a \(z = 0\). Ľahko overíme, že obe nájdené trojice \((0, 0, - 1)\) a \((- 1, 0, 0)\) sú riešeniami danej sústavy, rovnako aj trojica \((0, - 1, 0)\), ktorú dostaneme ich permutáciou.
Daná sústava má päť riešení: \((0, 0, - 1), (0, - 1, 0), ( - 1, 0, 0), (1 +\sqrt{2}, 1 +\sqrt{2}, 1 +\sqrt{2})\) a \((1 -\sqrt{2}, 1 -\sqrt{2}, 1 -\sqrt{2})\).
Komentár
Posledné dve úlohy seminára kombinujú princípy z prvých dvoch úloh: vhodné sčítanie a odčítanie rovníc medzi sebou a úpravu na súčin členov, ktorý je rovný nule. Dôležité však je, aby boli študenti pozorní pri vyvodzovaní záverov a pokryli v ich riešení všetky možnosti. Zároveň je posledná úloha pekným príkladom symetrie, je vhodné so študentami prediskutovať, ako táto úlohu zjednodušuje.Úloha 63-I-6
Riešenie*
Úloha 62-S-1
Riešenie*
Poznámka. Rovnostranný trojuholník so stranou \(a\) má výšku veľkosti \(v = \frac{1}{2}a \sqrt{3}\), takže skúmané polomery sú \(R =\frac{2}{3}v \big(=\frac{1}{3}a\sqrt{3}\big)\) a \(r =\frac{1}{3}v \big(=\frac{1}{6}a\sqrt{3}\big)\), a preto \[S = \pi ( R^2 - r^2) = \pi \big( \tfrac{4}{9} -\tfrac{1}{9})v^2= \pi \cdot \tfrac{1}{3}\cdot\tfrac{3}{4}a^2= \pi \big( \tfrac{1}{2}a\big)^2= T.\]
Komentár
Úloha je relatívne jednoduchá, využíva znalosť o bode dotyku vpísanej kružnice a taktiež pripravuje študentov na nasledujúcu zložitejšiu analýzu.Úloha 59-I-3-D2
Riešenie*
Úloha 63-I-1
Riešenie*
Hľadaná najmenšia hodnota výrazu \(V\) je teda rovná 8.
Komentár
Riešenie úlohy vyžaduje prácu so sústavou dvoch rovníc, avšak manipulácia tejto sústavy nie je až taká zložitá, takže zaradenie úlohy bez toho, aby sme sa systematicky venovali riešeniu sústav rovníc, nepokladáme za problematické.Úloha 62-I-2-N1
Riešenie
Úloha 58-II-1
a) Dokážte, že pre každé reálne číslo \(x\)platí \(V (x) \geq 3\).
b) Nájdite najväčšiu hodnotu \(V (x)\).
Riešenie
a) Keďže \(x^4 +1 > 0\) pre každé \(x\), nerovnosť \(V (x) \geq 3\) je ekvivalentná s nerovnosťou \(5x^4 - 4x^2 + 5 \geq 3(x^4 + 1)\), čiže \(2x^4 - 4x^2 + 2 \geq 0\). Výraz na ľavej strane je rovný \(2(x^2 - 1)^2\), takže je nezáporný pre každé \(x\).
b) Využime nasledujúcu úpravu: \[V (x) =\frac{5x^4 - 4x^2 + 5}{x^4 + 1}=\frac{5(x^4 +1)}{x^4 + 1}-\frac{4x^2}{x^4 + 1}=5-\frac{4x^2}{x^4 + 1}.\] Keďže zlomok \[\frac{4x^2}{x^4 + 1}\] je vďaka párnym mocninám premennej \(x\) pre ľubovoľné reálne číslo \(x\) nezáporný, nadobúda výraz \(V\) svoju najväčšiu hodnotu \(V_{max}\) práve vtedy, keď \[\frac{4x^2}{x^4 + 1}=0\] teda práve vtedy, keď \(x = 0\). Dostávame tak \(V_{max} = V (0) = 5\).
Úloha 59-I-6-N2
Riešenie*
Úloha 57-I-6
Riešenie*
Zrejme tiež \(c \neq 0\) (v opačnom prípade by platilo \(a = b = c = x = 0\)). Ostatné možnosti vyšetríme zostavením nasledujúcej tabuľky.
| \(c\) | \(9c\) | \(a+b+c\) | \(a+b\) |
|---|---|---|---|
| 1 | 9 | 9 | 8 |
| 2 | 18 | 8 | 6 |
| 3 | 27 | 7 | 4 |
| 4 | 36 | 6 | 2 |
Rovnosť [eq:57I6] možno prepísať na tvar \[\label{eq:57I6_2} 100(b - a - d) = 10d + a + 11b - 8c.\] Hodnota pravej strany je aspoň \(-72\) a menšia ako 200, lebo každé z čísel \(a, b, c, d\) je najviac rovné deviatim. Takže buď \(b - a - d = 0\), alebo \(b - a - d = 1\).
V prvom prípade po substitúcii \(d = b - a\) upravíme vzťah [eq:57I6_2] na tvar \(8c = 3(7b - 3a)\), z ktorého vidíme, že \(c\) je násobkom troch. Z prvej tabuľky potom vyplýva \(c = 3, a = 4 - b\), čo po dosadení do rovnice \(8c = 3(7b - 3a)\) vedie k riešeniu \(a = b = 2, c = 3\). Pôvodné číslo je teda \(x = 223\) a jeho deväťnásobok \(9x = 2 007.\)
V druhom prípade dosadíme \(d = b - a - 1\) do [eq:57I6_2] a zistíme, že \(8c + 110 = 3(7b-3a)\). Výraz \(8c+110\) je teda deliteľný tromi, preto číslo \(c\) dáva po delení tromi zvyšok 2. Dosadením jediných možných hodnôt \(c = 2\) a \(b = 6 - a\) do poslednej rovnice zistíme, že \(a = 0\), čo je v rozpore s tým, že číslo \(x = 100a + 10b + c\) je trojciferné.
Záver. Klárka dostala štvorciferné číslo 2 007.
Poznámka. Prvá tabuľka ponúka jednoduchší, ale numericky pracnejší postup priameho dosadzovania všetkých prípustných hodnôt čísel \(a, b, c\) do rovnice [eq:57I6]. Počet všetkých možností možno obmedziť na desať odhadom \(b \geq a\), ktorý zistíme pomocou vhodnej úpravy vzťahu [eq:57I6] napríklad na tvar [eq:57I6_2]. Riešenie uvádzame v druhej tabuľke.
| \(a\) | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 1 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(b\) | 7 | 6 | 5 | 4 | 5 | 4 | 3 | 3 | 2 | 1 |
| \(c\) | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 4 |
| \(9x\) | 1539 | 2349 | 3159 | 3969 | 1368 | 2178 | 2988 | 1197 | 2007 | 1026 |
Úloha 59-I-2-N2
Riešenie*
Úloha 65-I-3-N1
Riešenie*
Druhý výraz upravíme podobným spôsobom, obdržíme však súčet troch druhých mocnín: \(x^2+ 4y^2+ 3z^2- 2x - 12y - 6z + 13= (x^2-2x+1)+(4y^2-12y+9)+3(z^2-2z+1)=(x-1)^2+(2y-3)^2+3(z-1)^2\). Všetky tri sčítance sú nezáporné a teda aj ich súčet bude nezáporný a rovný nule bude v prípade, ak základy všetkých troch mocnín budú tiež rovné nule, teda \(x=1\), \(y=\frac{3}{2}\) a \(z=1\).
Pohľad na posledné dva členy posledného výrazu nám napovie, že pravdepodobne opäť využijeme podobnú úpravu ako v predchádzajúcich prípadoch, základy mocnín však budú obsahovať dve premenné. Skutočne rozpísaním člena \(2x^2=x^2+x^2\) a preusporiadaním poradia členov dostávame \((x^2-4xy+4y^2)+(x^2-2xy+z^2)\), odkiaľ je už zrejmé, že výraz bude mať tvar súčtu dvoch druhých mocnín \((x-2y)^2+(x-z)^2\). Výraz je vždy nezáporný a nulovú hodnotu nadobúda pre \(x=2y=z\).
Komentár
Cieľom úlohy je zopakovať použitie vzorcov \((A\pm B)^2\) v trochu menej priamočiarych mnohočlenoch než na aké je priestor v bežnom vyučovaní. Zároveň rozpísanie člena \(2x^2\) na súčet dvoch rovnakých členov je trik, na ktorý je vhodné študentov upozorniť, keďže tento princíp nájde uplatnenie v nejednej úlohe.Úloha 59-I-2-D2
Riešenie*
Úloha 65-I-3-D4
a) Dokážte, že pre každé reálne číslo \(x\) platí \(V (x) \geq 3\).
b) Nájdite najväčšiu hodnotu \(V (x)\).
Riešenie*
Úloha 65-I-6-D1
Riešenie*
Úloha 60-I-5-D2
Riešenie*
Úloha 63-I-3-N3
Riešenie*
Úloha 60-I-5-N2
Riešenie
Alternatívne môžeme vzťah dokázať úvahou o exponentoch prvočísel, z ktorých sú čísla \(a\) a \(b\) zložené. Nech \(a=p_1^{\alpha_1}\cdot p_2^{\alpha_2} \cdots p_k^{\alpha_k}\) a \(b=p_1^{\beta_1}\cdot p_2^{\beta_2} \cdots p_k^{\beta_k}\), kde \(p_1\) až \(p_k\) sú prvočísla a \(\alpha_k, \beta_k\) prirodzené čísla. Potom
\[\begin{aligned} (a,b) &=p_1^{\min\{\alpha_1, \beta_1\}}\cdot p_2^{\min\{\alpha_2, \beta_2\}}\cdots p_k^{\min\{\alpha_k, \beta_k\}},\\ [a,b] &=p_1^{\max\{\alpha_1, \beta_1\}}\cdot p_2^{\max\{\alpha_2, \beta_2\}}\cdots p_k^{\max\{\alpha_k, \beta_k\}},\\ ab &=p_1^{\alpha_1+\beta_1}\cdot p_2^{\alpha_2+\beta_2}\cdots p_k^{\alpha_k, \beta_k}.\end{aligned}\]
Keďže pre akékoľvek čísla \(\alpha, \beta\) platí \(\max\{\alpha, \beta\}+\min\{\alpha, \beta\}=\alpha+\beta\), a to vo všetkých prípadoch \(\alpha < \beta\), \(\alpha = \beta\), \(\alpha > \beta\), je naše tvrdenie dokázané.
Komentár
Predchádzajúce tvrdenie je stavebným kameňom mnohých úloh o spoločných násobkoch a deliteľoch, najmä myšlienka zápisu prirodzených čísel \(a\) a \(b\) v tvare \(a=ud\) a \(b=vd\), kde \(u\) a \(v\) sú prirodzené čísla také, že \((u,v)=1\) a \(d=(a,b)\) nájde uplatnenie veľmi často.Úloha 64-I-1
Riešenie*
Z prvej rovnice vidíme, že musí byť \(4 - y \geq 0\), teda \(y \leq 4\). V druhej rovnici môžeme teda odstrániť absolútnu hodnotu. Dostaneme tak \[|y - 4| = 4 - y = x + 8,\ \ \ \ \mathrm{ t.\,j.}\ \ \ \ - y = x + 4.\] Po dosadení za \(x + 4\) do prvej rovnice dostaneme \[|-y| = |y| = 4 - y.\] Keďže \(y \leq 4\), budeme ďalej uvažovať dva prípady.
Pre \(0 \leq y \leq 4\) riešime rovnicu \(y = 4 - y\), a teda \(y = 2\). Nájdenej hodnote \(y = 2\) zodpovedá po dosadení do druhej rovnice \(x = -6\).
Pre \(y < 0\) dostaneme rovnicu \(-y = 4 - y\), ktorá však nemá riešenie.
Záver. Daná sústava rovníc má práve jedno riešenie, a to \((x, y) = (-6, 2)\).
Iné riešenie*. Odstránením absolútnych hodnôt v oboch rovniciach, t. j. rozborom štyroch možných prípadov, keď
a) \((x + 4 \geq 0) \wedge (y - 4 \geq 0), \ \mathrm{ t.\,j.} \ (x \geq -4) \wedge (y \geq 4)\),
b) \((x + 4 \geq 0) \wedge (y - 4 < 0), \ \mathrm{ t.\,j.} \ (x \geq -4) \wedge (y < 4)\),
c) \((x + 4 < 0) \wedge (y - 4 \geq 0), \ \mathrm{ t.\,j.} \ (x < -4) \wedge (y \geq 4)\),
d) \((x + 4 < 0) \wedge (y - 4 < 0), \ \mathrm{ t.\,j.} \ (x < -4) \wedge (y < 4)\),
zistíme, že prípady a), b), c) nedávajú (vzhľadom na uvedené obmedzenia v jednotlivých prípadoch) žiadne reálne riešenie. V prípade d) potom dostaneme jediné riešenie \((x, y) = (-6, 2)\) danej sústavy.
Komentár
V úvode riešenia pripomenieme vzťah \(\sqrt{a^2}=|a|\), ktorý nám pomôže transformovať sústavu zo zadania na sústavu rovníc s absolútnou hodnotou, ktorú by študenti mali byť schopní bez väčších komplikácií vyriešiť.Úloha
Riešenie
Kadleček, Jiří. 1996. Geometrie V Rovině a V Prostoru: Pro Střední školy. Praha: Prometheus.
Úloha 62-I-3-N2
Riešenie*
Úloha 61-I-4-N2
Riešenie*
Úloha 63-I-3-N2
Riešenie
Úloha 66-I-1-N1
\(2xyz \leq x^2+ y^2z^2\),
\((x^2-y^2)^2\geq 4xy(x - y)^2\).
Riešenie
b) Výraz z pravej strany nerovnosti prevedieme na opačnú stranu a upravíme nasledujúcim spôsobom: \[\begin{aligned} ((x-y)(x+y))^2-4xy(x-y)^2 &\geq 0,\\ (x-y)^2(x+y)^2-4xy(x-y)^2 &\geq 0,\\ (x-y)^2((x+y)^2-4xy) &\geq 0,\\ (x-y)^2(x+2xy+y^2-4xy) &\geq 0,\\ (x-y)^4 &\geq 0.\end{aligned}\] Posledná nerovnosť je zrejme pravdivým tvrdením a pôvodná nerovnosť je tak dokázaná.
Komentár
Úloha neprináša žiadny nový princíp, je však dobrým tréningom práce s upravovaním výrazov, podobne ako úloha nasledujúca.Úloha B-61-II-3
Dokážte, že obsahy trojuholníkov \(ABC\) a \(PQK\) sú rovnaké.
Dokážte, že obvod trojuholníka \(ABC\) nie je väčší ako obvod trojuholníka \(PQK\).Kedy nastane rovnosť obvodov?
Riešenie*

Štvoruholník \(SLCM\) je štvorec so stranou dĺžky \(r\) a \(|AM| = x\), \(|BL| = y\). Obsah trojuholníka \(ABC\) je rovný súčtu obsahov trojuholníkov \(ABS\), \(BCS\) a \(CAS\), teda \[S_{ABC}=\frac{(x + y)r + (y + r)r + (x + r)r}{2}= (x + y + r)r.\] Obsah trojuholníka \(ABC\) je zároveň rovný \[S_{ABC}=\frac{|AC| \cdot |BC|}{2}=\frac{(x + r)(y + r)}{2}=\frac{xy}{2}+\frac{(x + y + r)r}{2}=\frac{xy}{2}+\frac{S_{ABC}}{2}.\] Odtiaľ dostávame \(S_{ABC} = xy\), čiže \(S_{ABC} = S_{PQK}\), čo sme mali dokázať.
b) V trojuholníku \(ABC\) sú dĺžky strán \(a = y + r\), \(b = x + r\), \(c = x + y\). Obvod trojuholníka \(ABC\) je \(a + b + |AB|\), obvod trojuholníka \(PQK\) je \(x\sqrt{2} + y\sqrt{2} + |PQ|\).
Zrejme platí \(|AB| \leq |PQ|\) (\(|AB|\) je vzdialenosťou rovnobežiek \(AP\), \(BQ\), (obr. 1). Rovnosť nastane jedine v prípade \(|AP| = |BQ|\), čiže \(x = y\). Ešte dokážeme, že \(a + b \leq x\sqrt{2} + y\sqrt{2}\), teda že \(a + b \leq c\sqrt{2}\). Posledná nerovnosť je ekvivalentná s nerovnosťou, ktorú dostaneme jej umocnením na druhú, pretože obe jej strany sú kladné. Dostaneme tak \(a^2 +b^2 +2ab \leq 2c^2\). Keďže v pravouhlom trojuholníku \(ABC\) platí \(a^2 + b^2 = c^2\), máme dokázať nerovnosť \(2ab \leq a^2 + b^2\), ktorá je však ekvivalentná s nerovnosťou \(0 \leq (a - b)^2\). Tá platí pre všetky reálne čísla \(a\), \(b\) a rovnosť v nej nastane jedine pre \(a = b\), t. j. \(x = y\).
Celkovo vidíme, že obvod trojuholníka \(ABC\) je menší alebo rovný obsahu trojuholníka \(PQK\) a rovnosť nastane práve vtedy, keď je pravouhlý trojuholník \(ABC\) rovnoramenný.
Úloha 63-I-3-N4
Riešenie
Komentár
Úvodné dve jednoduché úlohy majú prípravný charakter na úlohu nasledujúcu a sú skôr rozcvičkou, než náročnou aplikáciou vedomostí o prvočíslach.Úloha 58-I-2-D2
Riešenie
Úloha 62-I-3-D1
Riešenie*
Úloha 63-II-2
Riešenie*
Skupina \(A\) obsahuje všetkých hráčov, ktorí majú po dvoch výhrach a dvoch prehrách. Skupina \(B\) pozostáva z hráčov s jednou výhrou, jednou prehrou a dvoma remízami. Skupina \(C\) obsahuje hráčov so štyrmi remízami.
Vojto a Tomáš sú jediní víťazi, preto nepatria do skupiny \(C\). Nepatria ani do skupiny \(B\), pretože v opačnom prípade by s nimi museli všetci traja hráči zo skupiny \(C\) s horším výsledkom remizovať (a každý hráč skupiny B má len dve remízy).
Z toho vyplýva, že Vojto a Tomáš majú po dvoch výhrach a dvoch prehrách a skupina \(C\) je prázdna. Zvyšní traja hráči tak majú po jednej výhre, jednej prehre a dvoch remízach, ktoré museli uhrať navzájom medzi sebou.
Záver. Peter a Martin spolu remizovali.
Iné riešenie*. Využijeme (nadbytočný) údaj, že Vojto porazil Petra: Keby mali Vojto a Tomáš po jednej výhre, jednej prehre a dvoch remízach, musel by aj Peter patriť medzi víťazov turnaja. Jediný v poradí nižší celkový výsledok sú totiž štyri remízy, Peter však jednu partiu prehral, a tak musel aj jednu vyhrať. Vojto a Tomáš majú 1preto po dvoch výhrach a dvoch prehrách. Ak Peter prehral s Vojtom, musel poraziť Tomáša. (Nemohol mať dve prehry, keďže bol v poradí nižšie ako Tomáš a Vojto. Ani nemohol s Tomášom, ktorý žiadnu remízu nemá, remizovať.) Potrebný druhý bod získal dvoma remízami – s Martinom a nepomenovaným piatym hráčom.
Záver. Peter a Martin spolu remizovali.
Úloha 57-I-1
Riešenie*
Položme preto \(n = 2^a \cdot 3^b \cdot 5^c\), pričom \(a, b, c\) sú prirodzené čísla. Čísla \(\sqrt[3]{3n}\) a \(\sqrt[5]{5n}\) sú celé, preto je exponent \(a\) násobkom troch a piatich. Aj \(\sqrt{2n}\) je celé číslo, preto musí byť číslo \(a\) nepárne. Je teda nepárnym násobkom pätnástich: \(a \in \{15, 45, 75,\,\ldots\}\). Analogicky je exponent \(b\) taký násobok desiatich, ktorý po delení tromi dáva zvyšok 2: \(b \in \{20, 50, 80,\,\ldots\}\). Napokon \(c\) je násobok šiestich, ktorý po delení piatimi dáva zvyšok 4: \(c \in \{24, 54, 84,\,\ldots\}\). Z podmienky, že \(n\) je najmenšie, dostávame \(n = 2^{15} \cdot 3^{20} \cdot 5^{24}\).
Presvedčíme sa ešte, že dané odmocniny sú prirodzené čísla: \[\sqrt{2n} = 2^8 \cdot 3^{10} \cdot 5^{12},\ \ \ \sqrt[3]{3n} = 2^5 \cdot 3^7 \cdot 5^8, \ \ \ \sqrt[5]{5n} = 2^3 \cdot 3^2 \cdot 5^5.\]
Záver. Hľadaným číslom je \(n = 2^{15} \cdot 3^{20} \cdot 5^{24}\).
Komentár
Úloha je netradičným príkladom uplatnenia poznatkov o rozklade čísla na súčin prvočísel a vďaka návodnej úlohe by študenti mali byť dostatočne pripravení na jej samostatné riešenie.Úloha B-65-I-3
Riešenie*

[fig:B65I3_1]
polomeru \(r_1\) kružnice \(k_1\) je priamo úmerná dĺžke úsečky \(AS_1\) a podobne veľkosť \(r_2\) priamo úmerná dĺžke úsečky \(BS_2\). Keď zväčšíme polomer jednej z kružníc, musí sa nutne polomer druhej kružnice zmenšiť.
Kružnica \(k_2\) nemôže mať polomer väčší ako najväčšia kružnica, ktorú možno do trojuholníka \(ABC\) vpísať. Takou kružnicou je zrejme kružnica \(k\) do trojuholníka \(ABC\) vpísaná. A naopak najmenší polomer bude mať kružnica \(k_2\), ak zvolíme \(k_1 = k\). (Že v oboch opísaných prípadoch pre \(k_2 = k\) aj pre \(k_1 = k\) existuje príslušná kružnica \(k_1\), resp. \(k_2\), je vcelku zrejmé.)
Stačí teda vypočítať polomer \(r\) kružnice \(k\) do trojuholníka \(ABC\) vpísanej a polomer kružnice \(k_2\), ktorá sa dotýka kružnice \(k\) a strán \(AB\) a \(BC\) daného trojuholníka.
Polomer \(r\) vpísanej kružnice vypočítame napríklad zo vzorca \(2S_{ABC} = ro\), pričom \(S_{ABC}\) označuje obsah trojuholníka \(ABC\) a \(o\) jeho obvod. Obsah daného pravouhlého trojuholníka \(ABC\) s preponou \(AB\) je pri zvyčajnom označení dĺžok strán rovný \(\frac{1}{2}ab.\) Prepona v trojuholníku \(ABC\) má (v centimetroch) podľa Pytagorovej vety veľkosť \(c= \sqrt{a^2 + b^2}=\sqrt{3^2 + 4^2} = 5\). Maximálny polomer kružnice \(k_2\) je teda \[r =\frac{2S_{ABC}}{o}=\frac{ab}{a+b+c}=\frac{3\cdot 4}{3+4+5}= 1.\]
Pre výpočet polomeru \(r_2\) kružnice \(k_2\), ktorá sa dotýka kružnice \(k\) a strán \(AB\) a \(BC\), označme \(D\) a \(E\) body, v ktorých sa kružnice \(k\) a \(k_2\) dotýkajú strany \(AB\), a \(F\), \(G\) dotykové body kružnice k postupne so stranami \(BC\) a \(AC\) (obr. [fig:B65I3_2]). Keďže daný trojuholník je

[fig:B65I3_2]
pravouhlý, je \(S_1FCG\) štvorec so stranou dĺžky \(r = 1\), takže \(|BF| = |BD| = 2\) a podľa Pytagorovej vety \(|BS_1| =\sqrt{5}\). Z podobnosti pravouhlých trojuholníkov \(BES_2\) a \(BDS_1\) potom vyplýva \[\frac{r_2}{|BS_2|}=\frac{r}{|BS_1|}, \ \ \ \ \text{čiže} \ \ \ \ \frac{r_2}{\sqrt{5}- r_2 - 1}=\frac{1}{\sqrt{5}}.\] Po úprave tak pre hľadanú hodnotu neznámej \(r_2\) dostaneme lineárnu rovnicu \[r_2(\sqrt{5} + 1) =\sqrt{5}-1,\] ktorú ešte zjednodušíme vynásobením \(\sqrt{5}-1\). Zistíme tak, že najmenšia možná hodnota polomeru kružnice \(k_2\) je rovná \[r_2 = \frac{3-\sqrt{5}}{2}.\]
Úloha B-59-I-3-N2
Riešenie
Úloha 58-I-3-N2, resp. 54-I-5
Riešenie*
Čísla \(1 111 = 11\cdot 101\) a \(11111 = 41\cdot 271\) však majú vo svojom rozklade trojmiestne prvočísla, takže nemôžu byť súčinom dvojmiestnych čísel. Ostáva preto jediná možnosť: \[abc = k~\cdot 111 111 = k~\cdot 3 \cdot 7 \cdot 11 \cdot 13 \cdot 37.\] Pozrime sa, ako môžu byť prvočísla 3, 7, 11, 13, 37 rozdelené medzi jednotlivé činitele \(a, b, c\). Pretože súčiny \(37 \cdot 3\) a \(3 \cdot 7 \cdot 11\) sú väčšie ako 100, musí byť prvočíslo 37 samo ako jeden činiteľ a zvyšné štyri prvočísla 3, 7, 11, 13 musia byť rozdelené do dvojíc. Keďže aj súčin \(11 \cdot 13\) je väčší ako 100, prichádzajú do úvahy iba rozdelenia na činitele \(3 \cdot 11, 7 \cdot 13\) a 37, alebo na činitele \(3 \cdot 13\), \(7 \cdot 11\) a 37. K týmto činiteľom ešte pripojíme možné činitele z rozkladu číslice \(k\) a dostaneme riešenia dvoch typov: \[a = 33k_1, b = 91, c = 37k_2, \ \ \ \ \text {pričom} \ \ k_1 \in \{1, 2, 3\}, k_2 \in \{1, 2\},\] \[a = 39k_1, b = 77, c = 37k_2,\ \ \ \ \text{pričom}\ \ k_1 \in \{1, 2\}, k_2 \in \{1, 2\},\] Hľadaný počet trojíc čísel \(a, b, c\) je teda \(3 \cdot 2 + 2 \cdot 2 = 10\).
Komentár
Posledná úloha seminára je zaujímavá myšlienkou, že čísla, ktoré majú všetky cifry rovnaké, sú násobkami čísel 11, 111, 1111, …. Ďalšia analýza uplatní poznatky o rozklade čísla na súčin prvočísel a je tak ďalším príkladom úlohy, v ktorej musia študenti zapojiť vedomosti z predchádzajúcich seminárov.Úloha 65-I-3-D3
Riešenie*
Úloha 64-I-2-N1
Riešenie
Úloha 59-I-4-N1
Riešenie*
Úloha 66-I-2-D4
Riešenie*
Úloha 61-I-1-N3
Riešenie*
Úloha 66-I-4-D1
Riešenie*
Úloha 64-I-3
Riešenie*
Ak \(k = 0\), je počet kociek pokrývajúcich dva krížiky rovný nule, preto vyhrá Simona.
Ak \(0 < k \leq 32\), umiestni Simona krížiky napr. iba na biele políčka šachovnice. Potom pod žiadnou kockou nie sú dva krížiky, preto vyhrá Simona.
Ak \(k > 32\), pričom \(k\) je párne, umiestni Simona 32 krížikov na biele políčka a zvyšné krížiky kamkoľvek. Potom pod párnym počtom kociek sú dva krížiky (takých kociek je totiž práve \(k - 32\), pretože každá dominová kocka pokrýva jedno biele a jedno čierne políčko šachovnice), takže vyhrá Simona.
Ak \(32 < k \leq 61\), pričom k je nepárne, nenapíše Simona krížiky do troch políčok v jednom z ”bielych rohov“, t. j. do rohového bieleho a do dvoch susedných čiernych políčok, ale napíše ich do všetkých ostatných 31 bielych políčok a zvyšok do akýchkoľvek čiernych políčok (okrem spomenutých dvoch). Na bielych políčkach je teda nepárny počet krížikov a na čiernych párny počet krížikov. Okolo každého čierneho políčka s krížikom sú všetky biele políčka tiež s krížikom, preto každá kocka, ktorá zakrýva čierne políčko s krížikom, zakrýva dva krížiky. Iné kocky dva krížiky nezakrývajú. Preto opäť vyhrá Simona.
Ak \(k = 63\), dva krížiky nie sú iba pod jedinou kockou, preto v takom prípade vyhrá Lenka, a to bez potreby akejkoľvek stratégie.
Odpoveď. Pre každé \(0 \leq k \leq 64\), \(k \neq 63\), má vyhrávajúcu stratégiu Simona, pri \(k = 63\) vyhráva automaticky Lenka.
Úloha 58-I-6-D3
Riešenie*
Úloha B-60-I-1-N1
Riešenie*
Úloha 61-II-3
Riešenie*

[fig:61II3_1]
Teraz si všimneme, že pre dĺžky strán trojuholníka \(ADE\) platí \[|AD| : |DE| : |AE| = \frac{2}{3}a : \frac{1}{2}a : \frac{5}{6}a = 4 : 3 : 5,\] takže podľa (obrátenej časti) Pytagorovej vety má trojuholník \(ADE\) pravý uhol pri vrchole \(D\), a teda rovnobežník \(ABCD\) je obdĺžnik. Dotyčnica \(BC\) kružnice vpísanej štvoruholníku \(ABCE\) je teda kolmá na dve jej (navzájom rovnobežné) dotyčnice \(AB\) a \(CE\). To už zrejme znamená, že bod dotyku dotyčnice \(BC\) je stredom úsečky \(BC\) (vyplýva to zo zistenej kolmosti vyznačeného priemeru kružnice na jej vyznačený polomer).
Iné riešenie*. Ukážeme, že požadované tvrdenie možno dokázať aj bez toho, aby sme si všimli, že rovnobežník \(ABCD\) je v danej úlohe obdĺžnikom. Namiesto toho využijeme, že úsečka \(CE\) je stredná priečka trojuholníka \(ABF\), pričom \(F\) je priesečník polpriamok \(BC\) a \(AE\) (obr. [fig:61II3_2]), lebo \(CE \parallel AB\) a \(|CE| =\frac{1}{2}|AB|\). Označme preto \(a = |AB| = 2|CE|\),

[fig:61II3_2]
\(b = |BC| = |CF|\) a \(e = |AE| = |EF|\) (rovnosť \(2a = 3b\) použijeme až neskôr). Rovnako ako v prvom riešení využijeme rovnosť \(b+e = a+\frac{1}{2}a (=\frac{3}{2}a)\), ktorá platí pre dĺžky strán dotyčnicového štvoruholníka \(ABCE\). Kružnica jemu vpísaná sa dotýka strán \(BC\), \(CE\), \(AE\) postupne v bodoch \(P\), \(Q\), \(R\) tak, že platia rovnosti \[|CP| = |CQ|, \ \ \ \ |EQ| = |ER| \ \ \ \ \text{a tiež}\ \ \ \ |FP| = |FR|.\] Pre súčet zhodných dĺžok \(|FP|\) a \(|FR|\) teda platí \[\begin{aligned} |FP| + |FR| &= (b + |CP|) + (e + |ER|) = (b + e) + (|CP| + |ER|) =\\ &=\frac{3}{2}a + (|CQ| + |EQ|) = \frac{3}{2}a + \frac{1}{2}a = 2a,\end{aligned}\] čo znamená, že \(|FP| = |FR| = a\).
Teraz už riešenie úlohy ľahko dokončíme. Rovnosť \(|BP| =\frac{1}{2}b\), ktorú máme v našej situácii dokázať, vyplýva z rovnosti \[|BP| = |BF| - |FP| = 2b -a,\] keď do nej dosadíme zadaný vzťah \(a=\frac{3}{2}b\).
Komentár
Úloha nadväzuje na predchádzajúcu a využíva rovnosť súčtov dĺžok opačných strán dotyčnicového štvoruholníka. Ďalej študenti uplatnia buď Pytagorovu vetu alebo vedomosti o stredných priečkach v trojuholníku, čo úlohu činí zaujímavou z hľadiska pestrosti.Rovnosť sa odvodí rozpísaním dĺžok strán na ich úseky vymedzené bodmi dotyku vpísanej kružnice a následným využitím toho, že každé dva z týchto úsekov, ktoré vychádzajú z rovnakého vrcholu štvoruholníka, sú zhodné.↩︎
Úloha 62-II-3
Riešenie*
Komentár
Úloha je veľmi podobná tej, ktorou sme sa zaoberali na stretnutí, slúži tak na overenie toho, či si študenti princíp riešenia osvojili. Zároveň ale zadanie nie je zapísané priamo rovnosťou, takže úloha precvičí aj schopnosť transformovať slovný text na matematický zápis.Úloha 65-I-1
Riešenie*
Úloha B-59-S-1
Riešenie*
Z oboch nájdených riešení dostaneme tú istú dvojicu rovníc \(x(x - 2) = 3\), \(x(x + 2) = 3\). Korene prvej z nich sú čísla \(-1\) a \(3\), ich aritmetický priemer je \(1\). Korene druhej rovnice sú čísla \(1\) a \(-3\), ich aritmetický priemer je \(-1\).
Úloha 61-I-1-N2
Riešenie*
Úloha 60-I-2
Riešenie*
Podobne to funguje aj z druhej strany. Ak pre nejakú dvojicu prirodzených čísel \(x,y\) platí \(50 \mid 19x + 3y\), tak \(19x + 3y = 50l\) pre nejaké prirodzené číslo \(l\). Z tejto rovnosti vyjadríme číslo \(y\); dostaneme \(y = (50l - 19x)/3\) (ďalší postup by bol podobný, aj keby sme vyjadrili \(x\) namiesto \(y\)). Po dosadení dostaneme \[23x + y = 23x + \frac{50l - 19x}{3}=\frac{69x + 50l - 19x}{3}=\frac{50 \cdot (x + l)}{3}.\] O výslednom zlomku vieme, že je to prirodzené číslo. Čitateľ tohto zlomku je deliteľný číslom 50. V menovateli je len číslo 3, ktoré je nesúdeliteľné s 50, preto sa číslo 50 nemá s čím z menovateľa vykrátiť a teda číslo \(23x + y\) je deliteľné 50.
Iné riešenie*. Zrejme \(3 \cdot (23x + y) - (19x + 3y) = 50x\), čiže ak 50 delí jedno z čísel \(23x + y\) a \(19x + 3y\), tak delí aj druhé z nich.
Úloha 66-I-3-N1
Riešenie*

Úloha 57-I-4
obdĺžnik 2 cm \(\times\) 4 cm,
obdĺžnik \(\sqrt{2}\) cm \(\times 4 \sqrt{2}\) cm.
Riešenie*
b) Celková dĺžka strán všetkých dielov tangramu je \(10\sqrt{2}\) cm. Je teda rovná obvodu obdĺžnika, ktorý máme zložiť. Odtiaľ a z textu návodnej úlohy 1 vyplýva, že všetky strany dielov tangramu musia byť umiestnené na hranici Skladaného obdĺžnika. To však nie je možné, lebo protiľahlé strany kosodĺžnikového dielu majú vzdialenosť menšiu ako 1 cm, ale najmenšia vzdialenosť protiľahlých strán obdĺžnika je \(\sqrt{2}\) cm. Záver. Obdĺžnik 2 cm \(\times\) 4 cm sa z tangramu zložiť dá, obdĺžnik \(\sqrt{2}\) cm \(\times\) 4\(\sqrt{2}\) cm sa zložiť nedá.
Úloha 63-I-3
Riešenie*
Komentár
Úloha vyžaduje vhodnú manipuláciu rovnosti zo zadania a potom už len dostatočne pozornú analýzu vzniknutých možností.Úloha 66-I-3-N2
Riešenie*
Úloha 62-I-5-N1
b) Určte všetky prirodzené čísla m, pre ktoré je rozdiel \(m^6 - m^2\) deliteľný číslom 120.
Riešenie*
Úloha 61-I-5-N4
Riešenie*
Úloha 61-I-3-N4, resp. 50-II-1
Riešenie*
| \(d\) | \(u+1\) | \(v+1\) | \(u\) | \(v\) | \(a\) | \(b\) |
|---|---|---|---|---|---|---|
| 1 | 2 | 25 | 1 | 24 | 1 | 24 |
| 1 | 5 | 10 | 4 | 9 | 4 | 9 |
| 2 | 5 | 5 | 4 | 4 | 8 | 8 |
| 5 | 2 | 5 | 1 | 4 | 5 | 20 |
V prípade \(d=2\) dostaneme \(u=v=4\), to je však spor s tým, že \(u\) a \(v\) sú nesúdeliteľné. Preto má úloha práve tri riešenia.
Komentár
Úloha okrem vhodného zapísania čísel \(a\), \(b\) a \([a,b]\) vyžaduje ešte vhodnú úpravu rovnosti zo zadania, opäť tak kombinuje algebraické poznatky s poznatkami z oblasti teórie čísel.Úloha B-59-I-5
Riešenie*
Uhly \(ACD\) a \(ABD\) sú obvodové nad tetivou \(AD\), preto sú zhodné. Uhol \(FEC\) je zhodný s uhlom \(ECB\) (striedavé uhly) a ten je zhodný s obvodovým uhlom \(DAB\). Podľa vety \(uu\) sú teda trojuholníky \(ECF\) a \(ABD\) naozaj podobné.
Iné riešenie*. Obvodové uhly \(DAB\) a \(DCB\) sú zhodné, rovnako aj uhly \(ADC\) a \(ABC\), a preto sú trojuholníky \(ADE\) a \(CBE\) podobné. Odtiaľ vyplýva \(|AE|/|AD| = |CE|/|CB| = |CE|/|AB|\). Analogicky aj trojuholníky \(DEB\) a \(AEC\) sú podobné, odkiaľ \(|BE|/|BD| = |CE|/|AC| = |CE|/|AB|\). Z rovností \(|AE|/|AD| = |CE|/|AB|= |BE|/|BD|\) vyplýva podobnosť trojuholníka s dĺžkami strán \(|AE|\), \(|CE|\), \(|BE|\) s trojuholníkom \(ABD\).
Úloha 61-I-2-N4
Riešenie*
Úloha 60-I-3-D4
Riešenie*
Úloha 62-I-6-N1
Riešenie*
Úloha 64-I-1-N2
a) \(|x + 2| = y - 1, |y - 5| = -x \ \ [x = -3, y = 2]\)
b) \(|x - 1| = y, |x - 2| = y + 2\) [sústava nemá riešenie]
c) \(|x| = y + 1, x = |y| + 1 \ \ [x = 1, y = 0]\)
Riešenie*
Úloha B-66-I-5-N2
Riešenie*
Úloha 59-I-5-N2
Riešenie*
Úloha 64-I-3-N3
Riešenie
Komentár
Zaujímavé bude sledovať, ako efektívne sa budú študenti schopní zhostiť úlohy. Keďže má úloha jednoznačný číselný výsledok, môžeme po chvíli samostatnej práce nechať študentov porovnať svoje výsledky a pokúsiť zistiť pôvod prípadných nezrovnalostí.Úloha 59-I-3-N1
Riešenie
Úloha 66-I-6-D2
Riešenie*
Úloha 59-II-3
Riešenie*

[fig:59II3_1]
Poznámka. Existencia tetív \(NP\) a \(NQ\) v zadaní je zaručená vďaka predpokladu, že kružnica \(l\) má väčší polomer ako kružnica \(k\). Ak označíme \(C\) stred úsečky \(SM\) a \(E\) ten priesečník kružnice \(k\) s osou úsečky \(SM\), ktorý leží v polrovine \(SMO\), bude stred O kružnice \(l\) ležať na polpriamke \(CE\) až za bodom \(E\) (obr. [fig:59II3_2]). Ďalší priesečník \(N\) oboch

[fig:59II3_2]
kružníc preto padne do pásu medzi rovnobežkami \(SM\) a \(N_0 E\) v polrovine \(OCS\), pričom \(N_0\) je štvrtý vrchol kosoštvorca s vrcholmi \(S\), \(M\), \(E\). Na to stačí ukázať, že kružnica \(l\) pretne polpriamku \(EN_0\) až za bodom \(N_0\), teda že jej polomer \(OS\) je väčší ako dĺžka úsečky \(ON_0\). Toto porovnanie dvoch strán trojuholníka \(OSN_0\) jednoducho vyplýva z porovnania jeho vnútorných uhlov: uhol pri vrchole \(N_0\) je najväčší, lebo oba uhly pri protiľahlej strane \(OS\) sú menšie ako \(60^\circ\) (trojuholník \(ESN_0\) je rovnostranný). Ľahko nahliadneme, že každá z rovnobežiek uvedeného pásu pretína každú z oboch kružníc v dvoch bodoch (vždy súmerne združených podľa príslušnej osi kolmej na \(SM\)). Tým je dokázaná nielen existencia oboch tetív \(NP\) a \(NQ\), ale aj to, že ich krajné body \(P\) a \(Q\) ležia na rovnakej strane od bodu \(N\) (ako na obr. [fig:59II3_1]), lebo oba body zrejme ležia v polrovine opačnej k spomenutej polrovine \(OCS\).
Komentár
Diskusia v poznámke je len zaujímavým doplnkom úlohy, existencia tetív je totiž predpokladom zadania a nie je nutné ju dokazovať. Úloha využíva úvahu, že lichobežník, ktorého základne sú rovnobežné tetivy danej kružnice, je rovnoramenný, ktorá môže byť pre študentov zaujímavým uvedomením.Úloha 60-I-4-D2
a) Ukážte, že panovník môže rytierov rozsadiť k dvom stolom tak, aby každý rytier sedel pri rovnakom stole najviac s jedným nepriateľom.
b) Ukážte, že v prípade ľubovoľného takéhoto rozsadenia sedí pri každom stole najviac 16 rytierov. (Nepriateľstvo je vzájomný vzťah: Ak \(A\) je nepriateľom \(B\), tak aj \(B\) je nepriateľom \(A\).)
Riešenie*
Úloha 66-I-1-D3, resp. 58-I-6
Riešenie*
Úloha 57-I-2
Riešenie*
Analogicky zistíme zhodnosť trojuholníkov \(SBK\) a \(SBL\), ďalej \(SCL\) a \(SCM\), a nakoniec \(SDM\) a \(SDN\). Na základe uvedených zhodností môžeme položiť \[|\measuredangle BSK| = |\measuredangle BSL| = \beta, \ \ \ \ |\measuredangle CSL| = |\measuredangle CSM| = \gamma, \ \ \ \ |\measuredangle DSM| = |\measuredangle DSN| = \delta.\] Odtiaľ a z obr. 1 potom dostávame \[\begin{aligned}
|\measuredangle ASD| - |\measuredangle CSD| &= (\alpha + \delta)- (\gamma + \delta) = \alpha - \gamma =\\
&= (\alpha + \beta) - (\gamma + \beta) = |\measuredangle ASB| - |\measuredangle BSC| = 40^\circ.\end{aligned}\] Záver. \(|\measuredangle ASD| -|\measuredangle CSD| = 40^\circ\).
Komentár
Úloha je relatívne nezložitým úvodom do seminára a nadväzuje na posledné geometrické stretnutie, ktoré sa zaoberalo opísanými a vpísanými kružnicami trojuholníku. Pre úplnosť len dodajme, že štvoruholník, ktorému je možné vpísať kružnicu, sa nazýva dotyčnicový.Úloha 64-I-5-N2
Riešenie
Úloha 65-I-1-D2, resp. 55-II-4
Riešenie*
Komentár
Úloha opäť ukazuje, že upravenie podmienok zo zadania do vhodného tvaru, o ktorom môžeme ďalej diskutovať, je často kľúčovým krokom v riešení. V tomto prípade ide o podmienku \(q=kp+1\) a následný rozbor hodnôt v čitateli a menovateli zlomku. To by v študentoch malo umocniť dojem, že zručné narábanie s algebraickými výrazmi nájde svoje široké uplatnenie.Úloha 66-I-2-D3
Riešenie*
Úloha 62-I-2
Riešenie*
Komentár
Druhá z dvojice úloh, v ktorej majú študenti nájsť najväčšiu/najmenšiu hodnotu. Podobne ako v predchádzajúcej úlohe nám k tomu pomôže nezápornosť druhej mocniny reálneho čísla, tu ju však musíme skombinovať ešte s ďalšími závermi z úlohy. Predpokladáme, že úloha pre študentov bude výzvou a pravdepodobne budú potrebovať niekoľkých miestach poradiť (napr. skúmanie druhej mocniny súčtu \(S\) je netriviálnym nápadom).Úloha 60-II-3
Dokážte, že priamky \(KM\) a \(CM\) zvierajú pravý uhol.
Vypočítajte dĺžky ramien lichobežníka \(ABCD\).
Riešenie*
Bod \(L\) je stredom úsečky \(KC\), preto na osi súmernosti úsečky \(KM\) leží nielen výška rovnostranného trojuholníka \(KLM\), ale aj stredná priečka trojuholníka \(KMC\). Preto je priamka \(CM\) kolmá na \(KM\). Ostáva vypočítať dĺžky ramien lichobežníka \(ABCD\). Označme \(P\) stred úsečky \(EB\). Keďže \(CM\) je kolmá na \(KM\), je ťažnica \(CP\) kolmá na \(EB\), takže trojuholník \(EBC\) je rovnoramenný, a teda aj daný lichobežník \(ABCD\) je rovnoramenný. Dĺžku ramena \(BC\) teraz vypočítame z pravouhlého trojuholníka \(PBC\), v ktorom poznáme dĺžku odvesny \(PB\). Pre druhú odvesnu \(CP\) zrejme platí \[|CP| = \frac{3}{2} |CM| = 3\cdot \frac{\sqrt{3}}{2}|KM|,\] čo jednoducho vyplýva z vlastností trojuholníka \(KMC\). A keďže z podobnosti trojuholníkov \(KMC\) a \(APC\) máme \(|KM| =\frac{2}{3}|AP|\), dostávame (počítané v centimetroch) \[|CP| = 3\cdot \frac{\sqrt{3}}{2}|KM| = 3\cdot \frac{\sqrt{3}}{2}\frac{2}{3}|AP| =\sqrt{3}\frac{2}{3}|AB| = 12\sqrt{3}.\] Potom \[|BC| =\sqrt{|PB|^2 + |PC|^2} =\sqrt{36 + 12^2\cdot 3} = 6\sqrt{1 + 12} = 6\sqrt{13}.\] Ramená daného lichobežníka majú dĺžku \(6\sqrt{13}\) cm.
Alternatívny dôkaz kolmosti priamok KM a CM. Keďže bod \(L\) je stredom úsečky \(KC\) a zároveň \(|LK| = |LM|\), lebo trojuholník \(KLM\) je rovnostranný, leží bod \(M\) na Tálesovej kružnici nad priemerom \(KC\), takže trojuholník \(KMC\) je pravouhlý.
Úloha 60-I-2-D2
Riešenie
Úloha 62-I-4-N8
Riešenie*
Úloha 62-II-4
Riešenie*
V druhej časti riešenia ukážeme, že vyhovuje \(v = 11\). Všetkých 20 vrcholov dvadsaťuholníka rozdelíme na päť štvoríc vrcholov štvorcov \(A_1 A_6 A_{11} A_{16}, A_2 A_7 A_{12} A_{17}, A_3 A_8 A_{13} A_{18}, A_4 A_9 A_{14} A_{19}\) a \(A_5 A_{10} A_{15} A_{20}\). Ak teraz vyberieme ľubovoľne 11 vrcholov, budú vďaka nerovnosti \(11 > 5\cdot 2\) medzi vybranými aspoň tri vrcholy niektorého z piatich uvedených štvorcov (Dirichletov princíp). Ostáva dodať, že akékoľvek tri vrcholy štvorca zrejme tvoria pravouhlý rovnoramenný trojuholník.
Odpoveď. Hľadané najmenšie číslo v je rovné číslu 11.
Úloha 63-I-5
Riešenie*
Deliteľnosť tromi: Pretože číslo 2 013 je deliteľné tromi, stačí dokázať deliteľnosť tromi zmenšeného súčtu \[S - 2 013 = n^4 + 2n^2= n^2(n^2+ 2).\] V prípade \(3 \mid n\) je všetko jasné, v opačnom prípade je \(n = 3k \pm 1\) pre vhodné celé \(k\), takže platí \(3 \mid n^2 + 2\), lebo \(n^2 + 2 = 3(3k^2 + 2k + 1)\).
Deliteľnosť číslom 32: Keďže \(2 016 = 32 \cdot 63\), stačí dokázať deliteľnosť číslom 32 zmenšeného súčtu \[S - 2 016 = n^4+ 2n^2 - 3 = (n^2+ 1)^2 - 2^2= (n^2+ 3)(n2 - 1).\] Predpokladáme, že \(n\) je nepárne, teda \(n = 2k + 1\) pre vhodné celé \(k\), preto platí \[n^2+ 3 = (2k + 1)^2+ 3 = 4(k^2+ k + 1)\ \ \ \mathrm{a} \ \ \ n^2 - 1 = (2k + 1)^2 - 1 = 4k(k + 1).\] Odtiaľ vyplýva, že \(32 \mid (n^2 + 3)(n^2 - 1)\), lebo číslo \(k(k + 1)\) je párne.
Poznámka. Deliteľnosť číslom 32 sa dá dokazovať i bez vykonaného algebraického rozkladu trojčlena \(n^4 + 2n^2 - 3\), z ktorého po dosadení \(n = 2k + 1\) roznásobením dostaneme \[n^4+ 2n^2 - 3 = 16k^4+ 32k^3+ 32k^2+ 16k = 16k(k^3+ 2k^2+ 2k + 1).\] Pre párne \(k\) je deliteľnosť takto upraveného výrazu číslom 32 zrejmá. Pre nepárne \(k\) je zase párny súčet \(k^3 + 1\), takže je párny i druhý činiteľ \(k^3 + 2k^2 + 2k + 1\).
Úloha 65-S-3
Riešenie*

Iné riešenie*. Označme \(\alpha\) veľkosti vnútorných uhlov pri základni \(AC\) rovnoramenného trojuholníka \(SAC\). Potom jeho vonkajší uhol pri vrchole \(S\), čiže uhol \(CSB\), má veľkosť \(2\alpha\), ktorú má aj uhol \(CAD\), pretože polpriamka \(AB\) je jeho osou (obr. 1). Rovnoramenné trojuholníky \(ACD\) a \(SCB\) sa tak zhodujú vo vnútorných uhloch pri svojich hlavných vrcholoch \(A\) a \(S\), a sú teda podobné. Preto je pomer ich obvodov rovný pomeru dĺžok ich ramien, a ten má naozaj hodnotu menšiu ako 2, lebo ramená trojuholníka \(ACD\) sú kratšie ako priemer danej kružnice, zatiaľ čo ramená trojuholníka \(SCB\) majú dĺžku jej polomeru.
Úloha 60-I-3-D1
Riešenie*
Úloha B-66-I-5-N1
Riešenie*
Úloha B-65-I-5-N1
Riešenie*
Úloha 62-I-5-D1
Riešenie*
Úloha 58-I-4-N1
Riešenie

Úloha B-66-S-2
Riešenie*
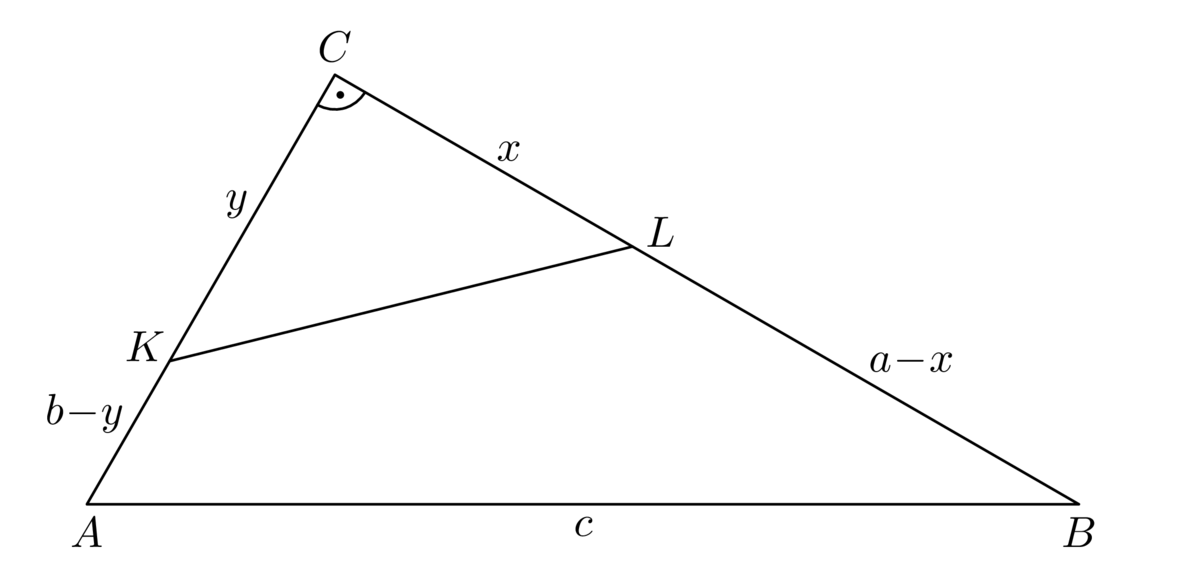
Použitím Pytagorovej vety v pravouhlom trojuholníku \(KLC\) dostaneme \(|KL|^2= x^2 + y^2\), takže skúmaný súčet môžeme upraviť nasledujúcim spôsobom: \[\begin{aligned} |AK|^2+ |KL|^2+ |LB|^2 & = (b - y)^2+ x^2+ y^2+ (a - x)^2=\\ & = 2x^2+ 2y^2 - 2ax - 2by + a^2+ b^2=\\ & = 2\bigg(x-\frac{a}{2}\bigg)^2+ 2\bigg( y -\frac{b}{2}\bigg)^2+\frac{a^2 + b^2}{2}=\\ & = 2\bigg(x -\frac{a}{2}\bigg)^2+ 2\bigg( y -\frac{b}{2}\bigg)^2+\frac{c^2}{2}.\end{aligned}\] Vďaka nezápornosti druhých mocnín z toho vidíme, že skúmaný výraz nadobúda svoju najmenšiu hodnotu, konkrétne \(\frac{1}{2}c\), práve vtedy, keď \(x =\frac{1}{2}a\) a súčasne \(y=\frac{1}{2}b\), teda práve vtedy, keď body \(K\), \(L\) sú postupne stredmi odvesien \(AC\), \(BC\) daného pravouhlého trojuholníka \(ABC\).
Záver. Najmenšia možná hodnota skúmaného súčtu je rovná \(\frac{1}{1}c^2\). Túto hodnotu dostaneme práve vtedy, keď body \(K\), \(L\) budú postupne stredmi odvesien \(AC\), \(BC\) daného pravouhlého trojuholníka.
Úloha 60-II-1
Riešenie*
Ak sú na tabuli aspoň dve nuly, ľahko sa presvedčíme, že súčet každých dvoch čísel z tabule je tam tiež. Dostávame, že trojica \(t, 0, 0\) je pre ľubovoľné reálne číslo \(t\) riešením úlohy.
Ak je na tabuli práve jedna nula, je tam trojica \(a, b, 0,\) pričom \(a\) aj \(b\) sú nenulové čísla. Súčet \(a + b\) teda nie je rovný ani \(a\), ani \(b\), musí preto byť rovný 0. Dostávame tak ďalšiu trojicu \(t, -t, 0\), ktorá je riešením úlohy pre ľubovoľné reálne číslo \(t\). Ak na tabuli nie je ani jedna nula, súčet \(a + b\) nie je rovný ani \(a\), ani \(b\), preto \(a + b = c\). Z rovnakých dôvodov je \(b + c = a\) a \(c + a = b\). Dostali sme sústavu troch lineárnych rovníc s neznámymi \(a, b, c\), ktorú môžeme vyriešiť. Avšak hneď z prvých dvoch rovníc po dosadení vyjde \(b + (a + b) = a\), čiže \(b = 0\). To je v spore s tým, že na tabuli žiadna nula nie je.
Záver. Úlohe vyhovujú trojice \(t, 0, 0\) a \(t, -t, 0\) pre ľubovoľné reálne číslo \(t\) a žiadne iné.
Úloha 61-I-3-N5
Riešenie*
Úloha 57-I-2-N2
Riešenie*
Úloha 61-I-5-N7
Riešenie*
Úloha 62-I-3
Riešenie*
V páse medzi priamkami AB a CD sú hľadanými bodmi práve tie, ktorých súčet vzdialeností od priamok \(BC\) a \(AD\) je rovný \(\frac{1}{6}o + |AB|\). Sú to teda body, ktoré ležia zvonka pásu určeného priamkami \(BC\) a \(AD\) a majú od bližšej z nich vzdialenosť rovnú \(\frac{2}{6}o : 2 = \frac{1}{12}o\). Množinu hľadaných bodov v páse medzi \(AB\) a \(CD\) tak tvoria dve úsečky \(B_1 C_1\) a \(A_1 D_1\) znázornené na . Ich krajné body \(A_1\), \(B_1\) ležia na priamke \(AB\) zvonka úsečky \(AB\) tak, že \(|AA_1 | = |BB_1 | =\frac{1}{12}o\); krajné body \(C_1\), \(D_1\) ležia na priamke \(CD\) zvonka úsečky \(CD\) tak, že \(|CC_1 | = |DD_1 | = \frac{1}{12}o\).
V páse medzi priamkami \(BC\) a \(AD\) sú hľadanými bodmi práve tie, ktorých súčet vzdialeností od priamok \(AB\) a \(CD\) je rovný \(\frac{1}{6}o + |BC|\). Sú to teda body, ktoré ležia zvonka pásu určeného priamkami \(AB\) a \(CD\) a ktoré majú od bližšej z nich vzdialenosť \(\frac{1}{12}o\). Množinu hľadaných bodov v páse medzi \(BC\) a \(AD\) tak tvoria dve úsečky \(A_2 B_2\) a \(C_2 D_2\), pritom krajné body \(B_2\), \(C_2\) ležia na priamke \(BC\) zvonka úsečky \(BC\) tak, že \(|BB_2 | = |CC_2 | =\frac{1}{12}o\) a krajné body \(A_2\), \(D_2\) ležia na priamke \(AD\) zvonka úsečky \(AD\) tak, že \(|AA_2 | = |DD_2 | =\frac{1}{12}o\).
Ostáva nájsť hľadané body mimo zjednotenia oboch uvažovaných pásov, teda body ležiace v nejakom zo štyroch pravých uhlov \(A_1 AA_2\), \(B_1 BB_2\), \(C_1 CC_2\), \(D_1 DD_2\). Z vyššie uvedených úvah vyplýva, že v každom z týchto uhlov hľadáme práve tie body, ktorých súčet vzdialeností od oboch ramien uhla je rovný hodnote \(\frac{1}{12}o\). Vzhľadom na symetriu ukážeme len to, že také body uhla \(A_1 AA_2\) vyplnia úsečku \(A_1 A_2\); v ostatných troch uhloch to potom budú úsečky \(B_1 B_2\), \(C_1 C_2\), \(D_1 D_2\) .
Všimnime si najskôr, že body \(A_1\), \(A_2\) sú jediné body na ramenách uhla \(A_1 AA_2\), ktoré majú požadovanú vlastnosť. Pre ľubovoľný vnútorný bod \(X\) uhla \(A_1 AA_2\) označme \(d_1\), \(d_2\) vzdialenosti bodu \(X\) od ramien \(AA_1\), resp. \(AA_2\). Hľadáme potom práve tie body \(X\), pre ktoré platí \(d_1 +d_2 =\frac{1}{12}o\) . Túto teraz vyriešime úvahou o obsahu S útvaru \(AA_1 XA_2\), ktorý je buď trojuholník, alebo konvexný či nekonvexný štvoruholník.
Obsah \(S\) je vždy rovný súčtu obsahov dvoch trojuholníkov \(AA_1 X\) a \(AA_2 X\): \[S = S_{AA_1 X} + S_{AA_2 X} =\frac{1}{2}|AA_1 |d_1 + \frac{1}{2}|AA_2 |d_2 = \frac{1}{2} \cdot \frac{1}{12}o \cdot (d_1 + d_2 ).\] Rovnica \(d_1 +d_2 =\frac{1}{12}o\) je tak splnená práve vtedy, keď obsah \(S\) má rovnakú hodnotu ako obsah \(S_0\) pravouhlého trojuholníka \(AA_1 A_2\), ktorého obe odvesny majú zhodnú dĺžku \(\frac{1}{12}o\). Hľadané body \(X\) sú teda práve tie, pre ktoré je útvar \(AA_1 XA_2\) trojuholník; ak je totiž \(AA_1 XA_2\) konvexný, resp. nekonvexný štvoruholník, platí zrejme \(S > S_0\), resp. \(S < S_0\). Hľadané body \(X\) uhla \(AA_1 A_2\) preto naozaj tvoria úsečku \(A_1 A_2\).
Odpoveď. Hľadaná množina je zjednotením ôsmich úsečiek, ktoré tvoria hranicu osemuholníka \(A_1 A_2 B_2 B_1 C_1 C_2 D_2 D_1\).
Poznámka. Z je tiež zrejmé, že rovnica \(d_1 + d_2 = c\), pričom \(c = |AA_1 | = |AA_2|\), bude splnená práve vtedy, keď bude \(|X_1 A_1 | = d_1\) a \(|X_2 A_2| = d_2\), t. j. práve vtedy, keď budú oba trojuholníky \(XX_1 A_1\) a \(XX_2 A_2\) rovnoramenné. To zrejme nastane práve vtedy, keď bude uhol \(A_1 XA_2\) priamy, pretože \(|\measuredangle AA_1 A_2 | = 45^\circ\).
Úloha 57-S-1
Riešenie*
Úloha 62-I-3-N1
Riešenie*
Úloha B-57-I-5-N3
Riešenie
Komentár
Jednoduchá úloha na úvod, v ktorej študenti aplikujú znalosti o závislosti medzi hodnotou diskriminantu a počtom riešení kvadratickej rovnice. Ten potom vedie na riešenie sústavy dvoch rovníc s dvomi neznámymi.Úloha 58-I-2-D1
Riešenie
Úloha 58-I-3-N3
Riešenie*
Úloha 64-II-4
a) Nájdite dve copaté čísla \(a, b\) také, že \(a \cdot b =2015\).
b) Rozhodnite, či existujú tri copaté čísla \(a, b, c\) také, že čísla \(a \cdot b\), \(b \cdot c\) a \(c \cdot a\) sú všetky prirodzené.
Riešenie*
Podobne vyhovuje každá z nekonečne veľa dvojíc \[a = 2 015 \cdot \frac{5^m}{2^n},\ \ \ b =\frac{2^n}{5^m},\] pričom \(m\) a \(n\) sú ľubovoľné prirodzené čísla. Uvedené číslo \(a\) má \(n\) desatinných miest, číslo \(b\) ich má \(m\).
b) Taká trojica copatých čísel neexistuje. Každé copaté číslo, ktoré má za desatinnou čiarkou poslednú nenulovú cifru na \(k\)-tom mieste, t. j. na mieste rádu \(10^{-k}\), môžeme pre vhodné prirodzené číslo s zapísať ako \(s \cdot 10^{-k} (k \geq 1)\). Pritom \(s\) nie je deliteľné desiatimi, môže teda byť deliteľné iba jedným z prvočísel 2 alebo 5, a to ľubovoľnou jeho mocninou.
Súčinom dvoch copatých čísel \(a = s/10^k\) a \(b = t/10^l\) dostaneme prirodzené číslo iba vtedy, keď je súčin \(st\) deliteľný \(10^{k+l}\) , čiže keď jedno z čísel \(s, t\) je deliteľné \(2^k+l\) a druhé \(5^k+l\), pričom \(k + l = 2\). Ak sú teda \(a = s/10^k\), \(b = t/10^l\), \(c = u/10^m\) ľubovoľné copaté čísla také, že súčiny \(a \cdot b\) a \(a \cdot c\) sú prirodzené čísla, je z predchádzajúcej úvahy zrejmé, že obe čísla \(t\) aj \(u\) musia byť buď obe nepárne a deliteľné piatimi, alebo naopak obe párne a nedeliteľné piatimi, takže ich súčin tu nemôže byť deliteľný desiatimi, teda súčin \(bc = tu/10^{l+m}\) nemôže byť celý.
Úloha 61-I-2-N5
Riešenie*
Úloha 65-II-1
Riešenie*
Záver. Hľadaná najmenšia možná hodnota daného výrazu je -32.
Úloha 64-S-3
Riešenie*
Ak je \(p = 5\), je \(q = p + 8 = 13\), takže \(r \in \{17, 19, 23, 29, 31,\,\ldots \}\) a \(n \in \{1 105,1 235, 1 495,\) \(1 885, 2 015,\,\ldots\}\). V tejto množine je zrejme najmenšie číslo s ciferným súčtom 8 číslo \(2 015\).
Ak je \(p > 5\), je \(p = 11\) najmenšie prvočíslo také, že aj \(q = p + 8\) je prvočíslo. Preto \(p = 11\), \(q = 19\), a teda \(r = 23\), takže pre zodpovedajúce čísla \(n\) platí \(n = 11 \cdot 19 \cdot 23= 4 807 > 2 015\).
Komentár
Úloha príjemne spája poznatky o deliteľnosti a prvočíslach a nemala by pre študentov byť neprekonateľnou výzvou.Úloha 58-S-3
Riešenie*
Vyriešme rovnicu [eq:58S3] vzhľadom na neznámu \(x\) (v ktorej je, na rozdiel od neznámej \(y\), rovnica lineárna): \[\begin{aligned} \label{eqs:58S3} 2x +\frac{x}{y}+ xy &= 2 009, \nonumber \\ 2xy + x + xy^2 &= 2 009y, \nonumber\\ x(y + 1)^2 &= 2 009y, \nonumber \\ x &= \frac{2009y}{(y + 1)^2}.\end{aligned}\] Hľadáme práve tie prirodzené čísla \(y\), pre ktoré má nájdený zlomok celočíselnú hodnotu, čo možno vyjadriť vzťahom \((y + 1)^2 \mid 2009y\). Keďže čísla \(y\) a \(y + 1\) sú nesúdeliteľné, sú nesúdeliteľné aj čísla \(y\) a \((y +1)^2\), takže musí platiť \((y +1)^2 \mid 2009 = 7^2 \cdot 41\). Keďže \(y +1\) je celé číslo väčšie ako 1 (a činitele 7, 41 sú prvočísla), poslednej podmienke vyhovuje iba hodnota \(y = 6\), ktorej po dosadení do [eqs:58S3] zodpovedá \(x = 246\). (Skúška nie je nutná, lebo rovnice [eq:58S3] a [eqs:58S3] sú v obore prirodzených čísel ekvivalentné.)
Hľadané čísla v uvažovanom poradí sú 246 a 6.
Komentár
Úloha je zaujímavá v tom, že na prvý pohľad nemusí riešiteľ tušiť, že ide o problém využívajúci poznatky z deliteľnosti. Zároveň vyžaduje netriviálnu zručnosť a nápad pri upravovaní počiatočnej rovnice do vhodného tvaru, nadväzuje tým na predchádzajúce semináre o algebraických výrazoch a rovniciach. Úloha je tak peknou ukážkou toho, že v matematike (a nielen tam) nie sú znalosti a koncepty nesúvisiace, ale často sú vzájomne prepojené.Úloha 62-I-1-D2
Riešenie*
Úloha 62-I-2-D2
Riešenie*
Úloha 57-S-3
Riešenie*
Ak má osoba \(A\) práve štyroch známych, napríklad osoby \(B\), \(C\), \(D\) a \(E\), existuje v Skupine osôb \(A\), \(B\), \(C\), \(D\), \(E\) najviac 10 známostí (, dvojice známych znázorňujú úsečky), a tak sa osoba \(F\) musí poznať s niektorou osobou \(X \in \{B, C, D, E\}\). Možnosť šírenia správy od ľubovoľnej osoby ku ktorejkoľvek inej ľahko overíme podľa .
Iné riešenie*. Znázornenie ktorejkoľvek množiny práve jedenástich dvojíc známych v Skupine šiestich osôb dostaneme odstránením štyroch z pätnástich hrán úplného grafu (, v ňom z každého uzla vychádza práve päť hrán). Po odstránení iba štyroch hrán z grafu na musí teda z každého vrcholu vychádzať aspoň jedna hrana. V Skupine teda neexistuje človek, ktorý by nikoho nepoznal. Aby sa preto správa nemohla od niektorej z osôb rozšíriť ku všetkým ostatným, musela by v príslušnom grafe existovať buď aspoň jedna oddelená dvojica, alebo dve oddelené trojice, v ktorých sa osoby môžu poznať navzájom. V žiadnej z týchto situácií však počet dvojíc známych neprevyšuje sedem, ako vidíme z . Tým je tvrdenie úlohy dokázané.
Úloha 60-I-5-D1
Riešenie*
Úloha B-66-I-3-N3
Riešenie*
Úloha 57-I-1-N1
Riešenie*
Komentár
Úloha je prípravou k riešeniu komplexnejšieho problému, ktorý nasleduje.Úloha 63-I-1-N1-N4
b) Určte najmenšiu možnú hodnotu výrazu \(W = 9 - ab\), kde \(a, b\) sú reálne čísla spĺňajúce podmienku \(a + b = 6\). Pre ktoré hodnoty \(a, b\) je \(W\) minimálne?
c) Určte najmenšiu možnú hodnotu výrazu \(Y = 12-ab\), kde \(a, b\) sú reálne čísla spĺňajúce podmienku \(a + b = 6\). Pre ktoré hodnoty \(a, b\) je \(Y\) minimálne?
d) Určte najväčšiu možnú hodnotu výrazu \(K = 5 + ab\), kde \(a, b\) sú reálne čísla spĺňajúce podmienku \(a + b = 8\). Pre ktoré hodnoty \(a, b\) je \(K\) maximálne?
Riešenie
a) Výraz \((x-2)^2\) je pre všetky reálne čísla \(x\) nezáporný, jeho minimálna hodnota tak je 0, v prípade \(x=2\). Najmenšia hodnota výrazu \(V\) je potom 5.
b) Z podmienky vyjadríme premennú \(a\) pomocou premennej \(b\), teda \(a=6-b\), dosadíme do \(W\) a upravíme použitím vzorca \((A-B)^2\): \(W=9-ab=9-(6-b)b=(b-3)^2\). Hodnota výrazu \(W\) je tak vždy nezáporná a \(W_{min}=0\), čo nastane pre \(b=3\) a \(a=3\).
c) Všimneme si, že \(Y=W+3\) a keďže aj podmienka je v tomto prípade rovnaká, platí \(Y=(b-3)^2+3\). Potom \(Y_{min}=3\) pre \(a=3\) a \(b=3\).
d) Podobne ako v predchádzajúcich častiach, vyjadríme z podmienky premennú \(a\) pomocou premennej \(b\): \(a=8-b\) a dosadíme do výrazu \(K\): \(K = 5 + 8a - a^2= -(a - 4)^2+ 21\), kde sme využili tzv. úpravu na štvorec. Vidíme, že časť \(-(a-4)^2\) je vždy nekladná, preto \(K_{max}=21\) pre \(a = b = 4\).
Komentár
V častiach c) a d) predchádzajúcej úlohy sme využili tzv. úpravu výrazu na štvorec. Aj napriek tomu, že tento úkon je v ŠVP zaradený až v neskoršej časti školského roka (v časti o kvadratických rovniciach), považujeme za vhodné študentov s metódou zoznámiť už teraz. Je totiž prirodzene spojená s úpravami výrazov, jej pochopenie je možné aj bez širších znalostí riešenia kvadratických rovníc a v úlohách MO nájde uplatnenie často.Úloha 58-S-2
Riešenie*
Zistili sme, že trojuholník \(ADC\) má pri vrcholoch \(C, D\) zhodné vnútorné uhly, je teda rovnoramenný, a preto \(|AD| = |AC|\).

Komentár
Úloha je zameraná na nájdenie veľkosti vhodných uhlov1 a využitie poznatku, že uhly pri základni rovnoramenného trojuholníka majú rovnakú veľkosť.V anglickej literatúre sa tejto metóde – počítaniu veľkostí všemožných uhlov – hovorí angle-chasing.↩︎
Úloha 59-S-2
Riešenie*

\(ACB\) (Tálesova veta). Trojuholníky \(ABC\) a \(AOD\) sú tak podobné podľa vety \(uu\), lebo sa zhodujú v uhloch \(ACB\), \(ADO\) a v spoločnom uhle pri vrchole \(A\). Z uvedenej podobnosti vyplýva \[\label{eq:59S2}
\frac{|BC|}{|OD|}=\frac{|AB|}{|AO|}.\] Zo zadaných číselných hodnôt vychádza \(|OD| = |OB| = 4\) cm, \(|OS| = |SB| - |OB| = 2\) cm, \(|OA| = |OS| + |SA| = 8\) cm a \(|AB| = 12\) cm. Podľa [eq:59S2] je teda \(|BC| : 4\,\text{cm} = 12 : 8\) a odtiaľ \(|BC| = 6\) cm. Z Pytagorovej vety pre trojuholník \(ABC\) nakoniec zistíme, že \(|AC| = \sqrt{12^2 - 6^2}\,\text{cm}= 6\) cm.
Úloha 58-I-6-N1
Riešenie*
Úloha 62-I-2-N1
Riešenie*
Poznámka. Dodajme, že upravená nerovnosť \[abc + a + b + c +\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{abc}\geq 8\] vyplýva okamžite aj z nerovnosti medzi aritmetickým a geometrickým priemerom ôsmich čísel \[abc, \ \ \ \ a, \ \ \ \ b, \ \ \ \ c, \ \ \ \ \frac{1}{a}, \ \ \ \ \frac{1}{b}, \ \ \ \ \frac{1}{c}, \ \ \ \ \frac{1}{abc},\] lebo ich súčin (a teda aj geometrický priemer) je rovný číslu 1, takže ich aritmetický priemer má hodnotu aspoň 1.
Iné riešenie*. V dokazovanej nerovnosti sa najskôr zbavíme zlomkov, a to tak, že obe jej strany vynásobíme kladným číslom \(abc\). Dostaneme tak ekvivalentnú nerovnosť \[(ab + 1)(bc + 1)(ac + 1) = 8abc,\] ktorá má po roznásobení ľavej strany tvar \[a^2b^2c^2 + a^2bc + ab^2c + abc^2 + ab + ac + bc + 1 \geq 8abc.\] Poslednú nerovnosť možno upraviť na tvar \[(abc -1)^2 + ab(c - 1)^2 + ac(b - 1)^2 + bc(a - 1)^2 \geq 0.\] Táto nerovnosť už zrejme platí, lebo na ľavej strane máme súčet štyroch nezáporných výrazov. Pritom rovnosť nastane práve vtedy, keď má každý z týchto štyroch výrazov nulovú hodnotu, teda práve vtedy, keď \[abc - 1 = c -1 = b - 1 = a - 1 = 0,\] čiže \[a = b = c = 1.\]
Iné riešenie*. Danú nerovnosť možno dokázať aj bez roznásobenia jej ľavej strany. Stačí napísať tri AG-nerovnosti \[\frac{1}{2}\bigg(a+\frac{1}{b} \bigg)\geq \sqrt{\frac{a}{b}}, \ \ \ \ \frac{1}{2}\bigg(b+\frac{1}{c} \bigg)\geq \sqrt{\frac{b}{c}}, \ \ \ \frac{1}{2}\bigg(c+\frac{1}{a} \bigg)\geq \sqrt{\frac{c}{a}},\] Ich vynásobením dostaneme \[\frac{1}{2}\bigg(a+\frac{1}{b} \bigg)\cdot\frac{1}{2}\bigg(b+\frac{1}{c} \bigg)\cdot \frac{1}{2}\bigg(c+\frac{1}{a} \bigg)\geq \sqrt{\frac{a}{b}} \cdot \sqrt{\frac{b}{c}}\cdot \sqrt{\frac{c}{a}} =1,\] odkiaľ po násobení ôsmimi obdržíme dokazovanú nerovnosť. Rovnosť v nej nastane práve vtedy, keď nastane rovnosť v každej z troch použitých AG-nerovností, teda práve vtedy, keď sa čísla v každej dvojici rovnajú: \[a =\frac{1}{b}, \ \ \ \ b =\frac{1}{c}, \ \ \ \ c =\frac{1}{a}.\] Z prvých dvoch rovností vyplýva \(a = c\), po dosadení do tretej rovnosti potom vychádza \(a = c = 1\), teda aj \(b = 1\).
Komentár
Študenti možno úlohu vyriešia iným spôsobom než využitím AG-nerovnosti. V tom prípade však riešenie predvedieme, aby študenti získali predstavu, ako sa táto nerovnosť dá efektívne využívať.Úloha 61-II-2
Riešenie*
Záver. Cifry na kartičkách sú 8, 2 a 1.
Poznámka. Riešiť odvodenú rovnicu \(26a + 2 = 64b + 73c\) pre neznáme (nenulové a navzájom rôzne) cifry \(a, b, c\) možno viacerými úplnými a systematickými postupmi, uviedli sme len jeden z nich.
Komentár
Úloha je zložitejšia než úvodné dve. Vychádza síce z rozvinutého zápisu čísla, avšak vyžaduje dodatočnú netriviálnu analýzu. Bude preto iste zaujímavé diskutovať so študentmi o tom, ako k pristupovali k riešeniu rovnice \(26a + 2 = 64b + 73c\).Úloha 66-I-5-prvá časť
Riešenie*

[fig:66I5_1]
Napriek tomu, že sa podľa obrázka zdá, že bod \(P\) na úsečke \(XY\) naozaj leží, musíme tento poznatok dokázať, teda odvodiť argumentáciou nezávislou na presnosti nášho rysovania. Na to určite stačí preukázať, že obe úsečky \(PX\), \(PY\) zvierajú s priamkou \(RT\) zhodné uhly (na obrázku vyznačené otáznikmi). Všimnime si, že tieto úsečky sú ťažnicami trojuholníkov \(RSP\) a \(TUP\), ktoré sa zhodujú vo vnútorných uhloch (vyznačených oblúčikmi) pri rovnobežných stranách \(RS\) a \(TU\), takže ide o trojuholníky podobné, a to s koeficientom \(k = |TU|/|RS|\). S rovnakým koeficientom platí aj podobnosť týchto trojuholníkov vyťatých ich ťažnicami, presnejšie podobnosť \(RXP \sim TYP\). Z nej už želaná zhodnosť uhlov \(RPX\) a \(TPY\) aj želaná rovnosť \(|PY | = k|PX|\) (vďaka rovnakému koeficientu) vyplýva. Všetko o bode \(P\) je tak dokázané; podobne sa overia aj obe vlastnosti bodu \(Q\) - ukáže sa, že úsečky \(QX\) a \(QY\) zvierajú ten istý uhol s priamkou \(RQ\) a ich dĺžky sú zviazané rovnosťou \(|QY | = k|QX|\), a to vďaka tomu, že \(QX\) a \(QY\) sú ťažnice v dvoch navzájom podobných trojuholníkoch \(RSQ\) a \(UTQ\).
Komentár
Úloha je prípravou na riešenie záverečného problému tohto seminára a pripomína študentom metódu dôkazu toho, že bod \(P\) leží na priamke úsečke \(XY\).Úloha 63-I-5-N1
Riešenie
a) \(n=3k\): \(n^3+2n=(3k)^3+2\cdot 3k=27k^3+6k=3k(9k^2+2)\), tvrdenie platí.
b) \(n=3k+1\): \(n^3+2n=(3k+1)^3+2(3k+1)=(27k^3+27k^2+9k+1)+(6k+2)=27k^3+27k^2+15k+3=3(9k^3+9k^2+5k+1)\), tvrdenie platí.
c) \(n=3k+2\): \(n^3+2n=(3k+2)^3+2(3k+2)=(27k^3+54k^2+36k+8)+(6k+4)=27k^3+54k^2+42k+12=3(9k^3+18k^2+14k+4)\), a preto \(3\mid n^3+2n\) aj v tomto prípade.
Iné riešenie. Môžeme sa inšpirovať predchádzajúcou úlohou a opäť využiť poznatok, že súčin troch po sebe idúcich čísel je vždy deliteľný tromi. Číslo \(n^3+2n\) môžeme napísať ako \(n^3-n+3n\). Číslo \(n^3-n\) je deliteľné tromi pre každé prirodzené \(n\), keďže ide o súčin troch po sebe idúcich čísel: \(n^3-n=n(n^2-1)=n(n-1)(n+1)\). \(3\mid 3n\) a preto aj \(3\mid n^3+2n\).
Komentár
Úloha zoznamuje študentov s ďalším možným postupom pri dokazovaní deliteľnosti výrazu daným prirodzeným číslom \(m\): rozdelenie na \(m\) možností podľa zvyšku po delení číslom \(m\) a dokázanie tvrdenia pre každú z týchto možností zvlášť. Je vhodné diskutovať so študentmi o výhodnosti tejto metódy pre (ne)veľké \(m\).V druhom prístupe k riešeniu sme využili to, že sme číslo \(2n\) zapísali v na prvý pohľad zložitejšom tvare \(-n+2n\), čo nám však v konečnom dôsledku pomohlo úlohu elegantne vyriešiť. Táto myšlienka nájde uplatnenie aj v iných úlohách (o.ı. aj v úlohe 7.10), preto ak s ňou študenti neprídu sami, je vhodné na ňu upozorniť.
Úlohu je možné dokázať použitím matematickej indukcie, avšak tá nie je štandardnou náplňou osnov nematematických gymnázií, preto sme toto riešenie nezvolili ako vzorové. Ak sa však študenti s dôkazom použitím indukcie stretli, je vhodné s nimi rozobrať aj tento spôsob riešenia.
Úloha 60-I-3
a) Dokážte, že \(S_B = S_D\).
b) Vypočítajte rozdiel \(S_C - S_A\).
c) Vysvetlite, prečo neplatí \(S_A + S_C = S_B + S_D\).
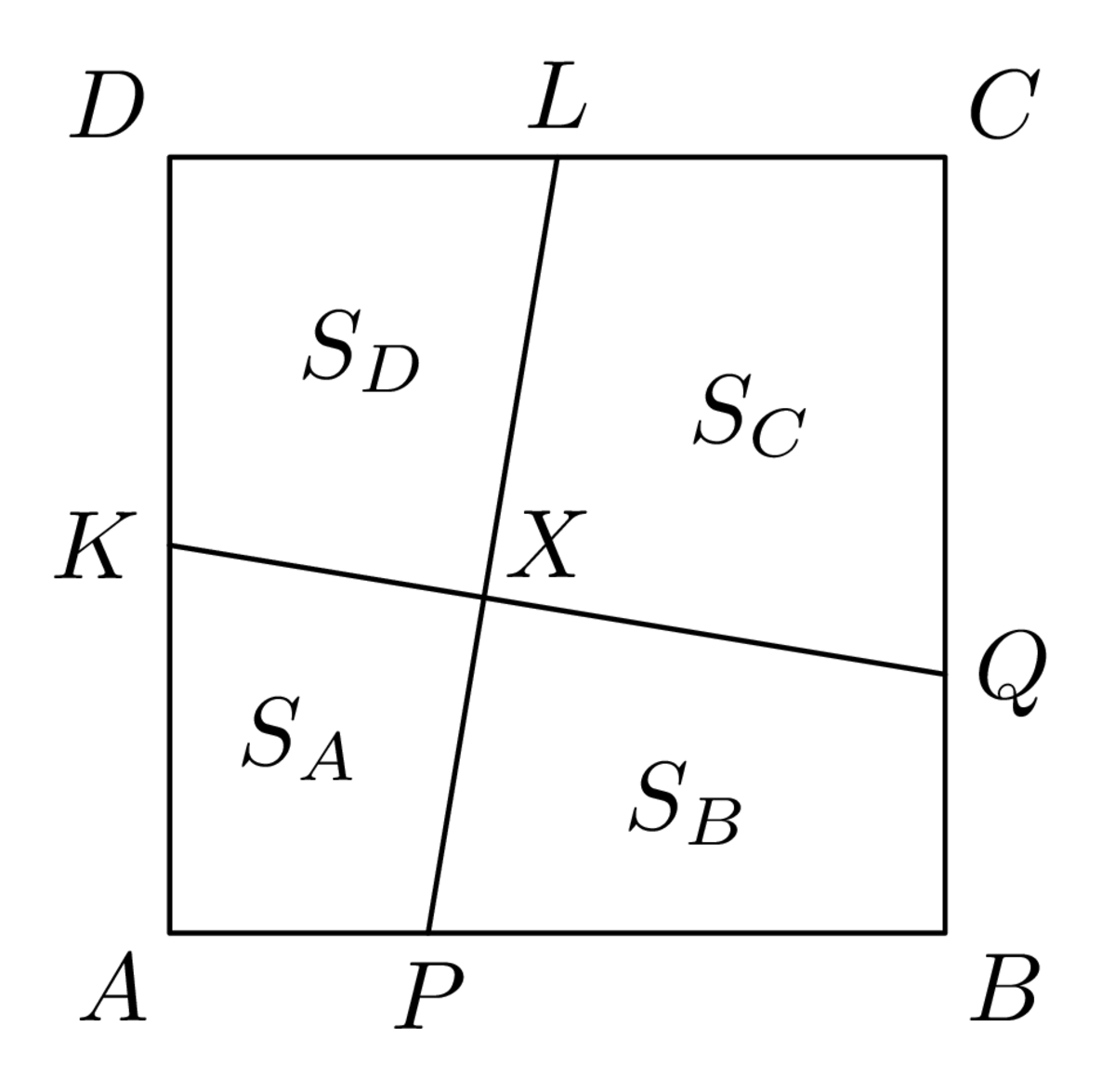
Riešenie*
b) Ľahko sa nám podarí vypočítať obsah pravouhlého lichobežníka \(ABQK\), lebo poznáme dĺžky základní aj výšku. Dostaneme \[S_A + S_B =\bigg( \frac{1}{2}+\frac{1}{3}\bigg)\cdot \frac{1}{2}=\frac{5}{12}\,\text{cm}^2.\] Podobne výpočtom obsahu lichobežníka \(PBCL\) dostaneme \[S_C + S_B =\bigg(\frac{1}{2}+\frac{2}{3}\bigg)\cdot\frac{1}{2}=\frac{7}{12}\,\text{cm}^2.\] Odčítaním prvej získanej rovnosti od druhej dostávame \(S_C - S_A =\frac{7}{12}-\frac{5}{12}=\frac{1}{6}\,\text{cm}^2\).
c) Nerovnosť medzi obsahmi \(S_A + S_C\) a \(S_B + S_D\) (ktorých priame výpočty nie sú v silách žiakov 1. ročníka) môžeme zdôvodniť nasledovným spôsobom: Súčet týchto dvoch obsahov je 1 cm\(^2\), takže sa nerovnajú práve vtedy, keď je jeden z nich menší ako \(\frac{1}{2}\) cm\(^2\). Bude to obsah \(S_B +S_D\) (rovný \(2S_B\), ako už vieme), keď ukážeme, že obsah \(S_B\) je menší ako \(\frac{1}{4}\) cm\(^2\). Urobíme to tak, že do celého štvorca \(ABCD\) umiestnime bez prekrytia štyri kópie štvoruholníka \(PBQX\). Ako ich umiestnime, vidíme na obr. [fig:60I3_2], pričom \(M\), \(N\) sú stredy strán \(BC\), \(AB\) a \(R\), \(S\) body, ktoré delia strany \(CD\), \(DA\) v pomere \(1 : 2\).

[fig:60I3_2]
[fig:60I3_3]
Iné riešenie* časti c). Tentoraz namiesto nerovnosti \(S_B + S_ D < \frac{1}{2}\) cm\(^2\) dokážeme ekvivalentnú nerovnosť \(S_A +S_C >\frac{1}{2}\) cm\(^2\). Preto sa pokúsime štvoruholník \(APXK\) tak, aby ležal pri štvoruholníku \(XQCL\) a aby sa ich obsahy dali geometricky sčítať. Uhly \(AKQ\) a \(DLP\) sú zhodné a \(| AK | = | DL |\), preto môžeme štvoruholník \(APXK\) premiestniť vo štvorci \(ABCD\) do jeho \(D\) tak, že k štvoruholníku \(XQCL\) priľahne pozdĺž strany \(LX\) svojou stranou \(LY\), pričom \(Y\) je priesečník úsečiek \(SM\) a \(PL\) z pôvodného riešenia (obr. [fig:60I3_3]). Obsah \(S_A + S_C\) je potom obsahom šesťuholníka \(DSYXQC\). Prečo je väčší ako \(\frac{1}{2}\) cm\(^2\), môžeme zdôvodniť napríklad takto:
Úsečka spájajúca bod \(L\) so stredom \(U\) úsečky \(KQ\) pretne úsečku \(SM\) v jej strede \(V\). Štvoruholník \(UQMV\) má obsah rovný polovici obsahu rovnobežníka \(KQMS\), teda rovný obsahu trojuholníka \(KMS\). Preto má šesťuholník \(DSV UQC\) obsah rovný obsahu štvoruholníka \(KMCD\), t. j. polovici obsahu štvorca \(ABCD\). Obsah \(S_A +S_C\) je ešte väčší, a to o obsah štvoruholníka \(XUVY\). Teda naozaj \(S_A + S_C >\frac{1}{2}\) cm\(^2\).
Komentár
Prvé dve časti sú príjemným úvahovým rozohriatím k časti tretej, ktorá vyžaduje trochu viac invencie. Demonštruje však zaujímavý prístup k riešeniu a porovnávanie obsahov obrazcov namiesto priameho výpočtu obsahov.Úloha B-58-S-1
Riešenie*
Daná sústava rovníc má riešenie iba pre dve hodnoty parametra \(a\), jednak pre \(a = -1\), keď je jej jediným riešením \((x, y) =\big(-\frac{1}{2}, \frac{3}{2}\big)\), jednak pre \(a=\frac{3}{2}\), keď \((x, y) = (2, -1)\).
Skúška dosadením je jednoduchá, možno ju vynechať takýmto zdôvodnením: Sústava dvoch rovníc, ktorú sme dostali (a vyriešili) sčítaním a odčítaním druhej a tretej rovnice, je s dvojicou pôvodných rovníc ekvivalentná. Zostávajúca (prvá) rovnica sústavy je potom ekvivalentná s kvadratickou rovnicou [eq:B58S1_2], ktorej riešením sme našli možné hodnoty parametra \(a\).
Úloha 63-I-6-N1
Riešenie*
Úloha B-62-II-4
Riešenie*
Poznámka. Akonáhle pomocou zhodných uhlov \(ALK\) a \(LKC\) zistíme, že priamky \(AB\) a \(CD\) sú rovnobežné, môžeme konštatovať, že oba tetivové štvoruholníky \(ADLK\) a \(BLKC\) sú buď pravouholníky, alebo rovnoramenné lichobežníky so zhodnými uhlami pri základniach. V oboch prípadoch to už zrejme zaručuje rovnobežnosť druhej dvojice priamok \(AD\) a \(BC\).
Úloha 60-II-4
Riešenie*
Iné riešenie*. Ukážeme, že ak je číslo \(x+y +z -xyz\) záporné, tak číslo \(xy +yz +zx-3\) je kladné. Predpokladajme, že \(x + y + z < xyz\). Tým skôr \(x < xyz\). Po skrátení kladného čísla \(x\) dostaneme \(yz > 1\). Podobne odvodíme odhady \(xy > 1\) a \(zx > 1\). Teraz ich stačí sčítať a máme \(xy + yz + zx > 3\).
Iné riešenie*. Tvrdenie úlohy dokážeme sporom. Predpokladajme, že \(x + y + z < xyz\) a zároveň \(xy + yz + zx < 3\). Obe tieto nerovnosti sú symetrické, preto môžeme predpokladať, že čísla \(x, y, z\) sú označené tak, že \(z\) je najmenšie. Z druhej nerovnosti dostaneme, že \(xy < 3\). Potom však \(x + y + z < xyz < 3z\), teda \(x + y < 2z\). To je však spor s tým, že číslo z je najmenšie.
Komentár
Úloha je zaujímavá tým, že na prvý pohľad nemusí vyzerať ako úloha o nerovnostiach a tiež študentom nemusí byť úplne jasné, z ktorého konca úlohu uchopiť. Môže to byť tiež dobrá príležitosť na ukážku toho, ako sa dá uplatniť dôkaz sporom.Úloha 66-I-1D3
Riešenie*
Úloha B-65-I-5-D1
Riešenie*
Úloha 66-I-4-N3
Riešenie*
Komentár
Úloha využíva takmer rovnaký princíp ako prvé dve seminárne úlohy, vyžaduje však dodatočnú analýzu plynúcu z poslednej podmienky, čo úlohe pridáva na náročnosti. Poslednou úlohou tejto gradovanej série je domáca práca, ktorej analýza povedie k riešeniu niekoľkých sústav troch rovníc s tromi neznámymi.Úloha 61-I-5-N8
Riešenie*
Úloha 60-II-2
Riešenie*
V prvom prípade máme \(n^2 + 6n = n^2 + 2n + 1\), teda \(4n = 1\), tomu však žiadne celé číslo \(n\) nevyhovuje.
V druhom prípade máme \(n^2 + 6n = n^2 + 4n + 4\), teda \(2n = 4\). Dostávame tak jediné riešenie \(n = 2\).
Iné riešenie*. Budeme skúmať rozklad \(n^2 + 6n = n(n+ 6)\). Spoločný deliteľ oboch čísel \(n\) a \(n + 6\) musí deliť aj ich rozdiel, preto ich najväčším spoločným deliteľom môžu byť len čísla 1, 2, 3 alebo 6. Tieto štyri možnosti rozoberieme.
Keby boli čísla \(n\) a \(n+6\) nesúdeliteľné, muselo by byť každé z nich druhou mocninou. Rozdiel dvoch druhých mocnín prirodzených čísel však nikdy nie je 6. Pre malé čísla sa o tom ľahko presvedčíme, a pre \(k = 4\) už je rozdiel susedných štvorcov \(k^2\) a \((k - 1)^2\) aspoň 7. Vlastnosť, že 1, 3, 4, 5 a 7 je päť najmenších rozdielov dvoch druhých mocnín, využijeme aj ďalej.
Ak je najväčším spoločným deliteľom čísel \(n\) a \(n+6\) číslo 2, je \(n = 2m\) pre vhodné \(m\), ktoré navyše nie je deliteľné tromi. Ak \(n(n + 6) = 4m(m + 3)\) je štvorec, musí byť aj \(m(m + 3)\) štvorec. Čísla \(m\) a \(m + 3\) sú však nesúdeliteľné, preto musí byť každé z nich druhou mocninou prirodzeného čísla. To nastane len pre \(m = 1\), čiže \(n = 2\). Ľahko overíme, že \(n(n + 6)\) je potom naozaj druhou mocninou celého čísla.
Ak je najväčším spoločným deliteľom čísel \(n\) a \(n + 6\) číslo 3, je \(n = 3m\) pre vhodné nepárne \(m\). Ak \(n(n+6) = 9m(m+2)\) je štvorec, musia byť nesúdeliteľné čísla \(m\) a \(m+2\) tiež štvorce. Také dva štvorce však neexistujú.
Ak je najväčším spoločným deliteľom čísel \(n\) a \(n + 6\) číslo 6, je \(n = 6m\) pre vhodné \(m\). Ak \(n(n + 6) = 36m(m + 1)\) je štvorec, musia byť štvorce aj obe nesúdeliteľné čísla \(m\) a \(m + 1\), čo nastane len pre \(m = 0\), my však hľadáme len kladné čísla \(n\).
Úlohe vyhovuje jedine \(n = 2\).
Komentár
K správnemu riešeniu úlohy vedú mnohé cesty. Prvé uvedené riešenie je trochu trikové, avšak nápadité, a preto ak ho študenti neobjavia, je vhodné im ho na záver ukázať. Nie je tiež nepravdepodobné, že študenti budú skúšať, ako sa číslo \(n^2+6n\) správa pre rôzne hodnoty \(n\), čo by ich mohlo naviesť na správu cestu nájdenia jediného riešenia.Úloha 58-I-5
Riešenie*
\[\begin{aligned} T_0 &= \{11, 22, 33, . . . , 99\},\\ T_1 &= \{1, 12, 23, . . . , 89\},\\ T_2 &= \{2, 13, 24, . . . , 90\},\\ \vdots\\ T_{10} &= \{10, 21, 32, . . . , 98\}.\\\end{aligned}\]
Ak vyberieme jedno číslo z \(T_0\) (viac ich ani vybrať nesmieme) a všetky čísla z \(T_1, T_2, T_3, T_4\) a \(T_5\), dostaneme vyhovujúci výber \(1 + 5 \cdot 9 = 46\) čísel, lebo súčet dvoch čísel z \(0, 1, 2, 3, 4, 5\) je deliteľný jedenástimi jedine v prípade 0 + 0, z množiny \(T_0\) sme však vybrali iba jedno číslo.
Na druhej strane, v ľubovoľnom vyhovujúcom výbere je najviac jedno číslo zo skupiny \(T_0\) a najviac 9 čísel z každej zo skupín \[T_1 \cup T_{10}, \ \ T_2 \cup T_9, \ \ T_3 \cup T_8, \ \ T_4 \cup T_7, \ \ T_5 \cup T_6,\] lebo pri výbere 10 čísel z niektorej skupiny \(T_i \cup T_{11-i}\) by medzi vybranými bolo niektoré číslo zo skupiny \(T_i\) a aj niektoré číslo zo skupiny \(T_{11-i}\); ich súčet by potom bol deliteľný jedenástimi. Celkom je teda vo výbere najviac \(1 + 5 \cdot 9 = 46\) čísel.
Poznámka. Možno uvedené riešenie vyzerá príliš trikovo. Avšak počiatočné úvahy každého riešiteľa k nemu rýchlo vedú: iste záleží len na zvyškoch vybraných čísel, takže rozdelenie na triedy \(T_i\) a vyberanie z nich je prirodzené. Je jasné, že z \(T_0\) môže byť vybrané len jedno číslo a všetko ďalšie, o čo sa musíme starať, je požiadavka, aby sme nevybrali zároveň po čísle zo skupiny \(T_i\) aj zo skupiny \(T_{11-i}\). Ak je už vybrané niektoré číslo z triedy \(T_i\), kde \(i\neq 0\), môžeme pokojne vybrať všetky čísla z \(T_i\), to už skúmanú vlastnosť nepokazí. Je preto dokonca jasné, ako všetky možné výbery najväčšieho počtu čísel vyzerajú.
Komentár
Je veľmi vhodné sa k tejto úlohe v nasledujúcom seminári vrátiť s poznámkou, že množiny \(T_1,\,\ldots, T_{10}\) nazývame zvyškové triedy.Úloha B-66-I-3
Riešenie*
Tetivový štvoruholník \(ABCD\) je teda rovnoramenný lichobežník či pravouholník, v ktorom sú (zhodné) trojuholníky \(DAB\) a \(ADC\) súmerne združené podľa spoločnej osi \(o_1\) strán \(AD\), \(BC\). Tá však prechádza stredom \(O\) kružnice \(k\). V uvedenej súmernosti si tak zodpovedajú aj ťažiská \(K\) a \(L\) oboch zhodných trojuholníkov \(DAB\) a \(ADC\) . Os úsečky \(KL\) teda prechádza stredom \(O\) kružnice \(k\). Navyše oba body \(K\) a \(L\) sú rôzne, pretože zodpovedajúce si ťažnice z (rôznych) vrcholov \(B\) a \(C\) sa pretínajú v strede spoločnej strany \(AD\) oboch zhodných trojuholníkov, zatiaľ čo ťažiská sú vnútornými bodmi oboch úsečiek.
Analogicky dokážeme, že aj \(ABDE\) je rovnoramenný lichobežník či pravouholník. Pre ťažiská \(K\), \(M\) zhodných trojuholníkov \(DAB\) a \(BED\) preto platí, že aj os úsečky \(KM\) prechádza stredom \(O\) kružnice \(k\). Odtiaľ \(|OL| = |OK| = |OM| > 0\) (body \(K\) a \(L\) sú rôzne), takže ťažiská všetkých troch uvažovaných trojuholníkov ležia na kružnici sústrednej s \(k\). Tým je dôkaz ukončený.
Úloha 66-S-3
Riešenie*
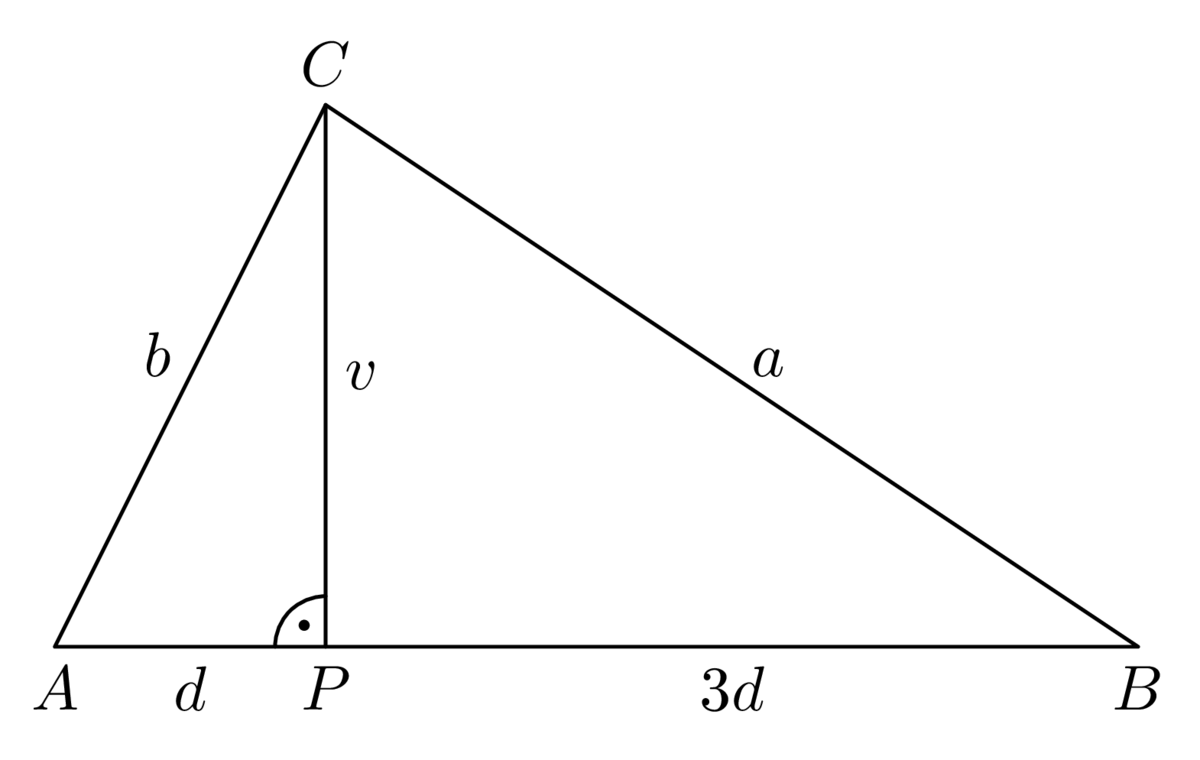
Použitím Pytagorovej vety v trojuholníkoch \(APC\) a \(PBC\) dostávame rovnosti \(b^2= d^2 +v^2\) a \(a^2 = 9d^2 +v^2\). Z druhého predpokladu úlohy potom vyplýva rovnosť \(a^2 = 3b^2\), čiže \(9d^2 + v^2 = 3d^2 + 3v^2\), odkiaľ \(v^2 = 3d^2\). Dosadením do prvých dvoch rovností tak dostávame \(a^2 = 12d^2\) a \(b^2 = 4d^2\). A keďže \(c = 4d\), čiže \(c^2 = 16d^2\), dokázali sme, že pre dĺžky strán trojuholníka \(ABC\) platí \(a^2 + b^2 = c^2\).
Trojuholník \(ABC\) je preto podľa obrátenej Pytagorovej vety pravouhlý.
Poznámka. Ak zvážime pomocný pravouhlý trojuholník s odvesnami \(a\) a \(b\), tak pre jeho preponu \(c'\) podľa Pytagorovej vety platí \(c' = a^2 + b^2\). Porovnaním s odvodenou rovnosťou \(c^2 = a^2 + b^2\) tak dostávame \(c'= c\), takže pôvodný trojuholník je podľa vety \(sss\) zhodný s trojuholníkom pomocným, a je teda skutočne pravouhlý. Môžeme tolerovať názor, že samotná Pytagorova veta udáva nielen nutnú, ale aj postačujúcu podmienku na to, aby bol daný trojuholník pravouhlý.
Komentár
Úloha relatívne priamočiaro využíva viacnásobné využitie Pytagorovej vety, je tak vhodným zahrievacím problémom tohto seminára.Úloha 59-I-4
Riešenie*

\(CST\) a \(SPT\) vyplýva \[\label{eq:59I4} |ST|^2 = s^2 - r^2\ \ \ \ \text{a} \ \ \ \ |ST|^2 = |SP|^2 + (s~-r)^2.\] Odtiaľ pre veľkosť úsečky \(SP\) vychádza \[|SP|^2 = (s^2 - r^2 ) - (s~- r)^2 = 2r(s - r).\] A keďže \(ABPS\) je pravouholník, dostávame \[|AB| = |SP| =\sqrt{2r(s - r)}.\]
Z pravouhlých trojuholníkov \(AMS\) a \(MTS\) ďalej podľa prvej rovnosti v [eq:59I4] vyplýva \[|AM|^2 = |SM|^2 - r^2 = |MT|^2- |ST|^2 - r^2 = |MT|^2 -s^2,\] pritom z pravouhlého trojuholníka \(MBT\) máme \[|BM|^2 = |MT|^2 - s^2.\] Preto \(|AM| = |BM|\) a bod \(M\) je teda stredom úsečky \(AB\).
Poznámka. Záver, že \(M\) je stredom úsečky \(AB\), vyplýva okamžite aj z mocnosti bodu \(M\) k obom kružniciam (bod \(M\) leží na tzv. chordále oboch kružníc). Tieto pojmy sú však pre súťažiacich kategórie C zväčša neznáme a nebudú nutné ani pre riešenia ďalších súťažných kôl.
Úloha B-59-I-5-N1
Riešenie
Úloha 61-I-3
Riešenie*
Podľa uvedených zistení môžeme čísla \(a, b, c\) usporiadať tak, že rozklady čísel \(a, b\) obsahujú po jednom exemplári prvočísla 5 (potom \((c, 5) = 1\)) a že \((a, 2) = 2\) (ako vieme, aspoň jedno z čísel \(a, b\) musí byť párne). Číslo 5 z množiny \(M\) je potom nutne rovné \((a, b)\), takže platí \((b, 2) = 1\), a preto \((b, 3) = 3\) (inak by platilo \((b, c) = 1\)), odtiaľ zase s ohľadom na \((a, b) = 5\) vyplýva \((a, 3) = 1\). Máme teda \(a = 5 \cdot 2^s\) a \(b = 5 \cdot 3^t\) pre vhodné prirodzené čísla \(s\) a \(t\).
Z rovnosti \([a, b] = 2^s \cdot 3^t \cdot 5\) vyplýva, že nastane jeden z troch nasledujúcich prípadov.
(1) \(2^s \cdot 3^t \cdot 5 = 60 = 2^2 \cdot 3^1 \cdot 5\). Vidíme, že platí \(s = 2\) a \(t = 1\), čiže \(a = 20\) a \(b = 15.\) Ľahko určíme, že tretím číslom je \(c = 18\).
(2) \(2^s \cdot 3^t \cdot 5 = 90 = 2^1 \cdot 3^2 \cdot 5\). V tomto prípade \(a = 10\), \(b = 45\) a \(c = 12\).
(3) \(2^s \cdot 3^t \cdot 5 = 180 = 2^2 \cdot 3^2 \cdot 5\). Teraz \(a = 20\), \(b = 45\) a \(c = 6\).
Záver. Hľadané čísla \(a, b, c\) tvoria jednu z množín \(\{20, 15, 18\}\), \(\{10, 45, 12\}\) a \(\{20, 45, 6\}\).
Iné riešenie*. V danej rovnosti je množina napravo tvorená šiestimi rôznymi číslami väčšími ako 1, takže čísla \((a, b), (a, c), (b, c)\) musia byť netriviálnymi deliteľmi postupne čísel \([a, b], [a, c], [b, c]\). Čísla 2, 3, 5 ale žiadne netriviálne delitele nemajú, musí teda platiť \[\{(a, b), (a, c), (b, c)\}= \{2, 3, 5\} \ \ \ \text{a} \ \ \ \{[a, b], [a, c], [b, c]\} = \{60, 90, 180\}.\] Pretože poradie čísel \(a, b, c\) nehrá žiadnu úlohu, môžeme predpokladať, že platí \((a, b) = 2, (a, c) = 3\) a \((b, c) = 5\). Odtiaľ vyplývajú vyjadrenia \[a = 2 \cdot 3 \cdot x = 6x, \ \ \ b = 2 \cdot 5 \cdot y = 10y, \ \ \ c = 3 \cdot 5 \cdot z~= 15z\] pre vhodné prirodzené čísla \(x, y, z\). Zo známej rovnosti \([x, y]\cdot(x, y) = xy\) tak dostaneme vyjadrenia najmenších spoločných násobkov v tvare \[[a, b] =\frac{6x \cdot 10y}{2}= 30xy, \ \ \ [a, c] =\frac{6x \cdot 15z}{3}= 30xz,\ \ \ [b, c] =\frac{10y \cdot 15z}{5}= 30yz.\] Z rovnosti \(\{30xy, 30xz, 30yz\} = \{60, 90, 180\}\) upravenej na \(\{xy, xz, yz\} = \{2, 3, 6\}\) potom vďaka tomu, že 2 a 3 sú prvočísla, vyplýva \(\{x, y, z\} = \{1, 2, 3\}\). Pretože z podmienky \(5 = (b, c) = (10y, 15z)\) vyplýva \(y \neq 3\) a \(z \neq 2\), prichádzajú do úvahy len trojice \((x, y, z)\) rovné (1, 2, 3), (2, 1, 3) a (3, 2, 1), ktorým postupne zodpovedajú trojice \((a, b, c)\) rovné (6, 20, 45), (12, 10, 45), (18, 20, 15). Skúškou sa presvedčíme, že všetky tri vyhovujú množinovej rovnosti zo zadania úlohy.
Úloha 58-II-4
Riešenie*
\(EDO\) je zrejme tiež pravouhlý, pretože jeho strany \(DO\) a \(EO\) sú kolmé na odvesny trojuholníka \(ABC\); pritom jeho výškou na preponu je úsečka \(OC\) (s veľkosťou \(\frac{1}{2}c\)). Vzhľadom na súmernosť úsečky \(AC\) podľa osi \(OD\) platí pre jeho uhol pri vrchole \(D\), že \(|\measuredangle CDO| = 90^\circ - |\measuredangle COD| = 90^\circ - |\measuredangle AOD| = \alpha\). Trojuholníky \(EDO\) a \(ABC\) sú teda podobné (\(uu\)). Koeficient k tejto podobnosti je daný pomerom dĺžok zodpovedajúcich výšok na prepony, takže \(k = |OC|/v = \frac{1}{2}c/v\), a keďže \(vc = 2S\), je \[k =\frac{c^2}{4S}.\] V uvedenej podobnosti zodpovedá prepone \(AB\) prepona \(DE\), preto pre jej veľkosť platí \[|DE| = kc =\frac{c^3}{4S}.\]
Iné riešenie*. Zo súmernosti dotyčníc z bodu ku kružnici vyplýva, že oba trojuholníky \(ACD\) aj \(BCE\) sú rovnoramenné, \(|AD| = |DC|\), \(|BE| = |CE|\). Rovnoramenné sú aj trojuholníky \(ACO\) a \(BCO\), pričom \(O\) je stred prepony \(AB\) (ramená oboch trojuholníkov majú veľkosť polomeru kružnice opísanej pravouhlému trojuholníku \(ABC\), čo je \(\frac{1}{2}c\)). Ukážeme, že ide o dve dvojice podobných trojuholníkov \(ACD \backsim BCO\) a \(ACO \backsim BCE\). K tomu si stačí všimnúť, že v štvoruholníku \(AOCD\), ktorý je zložený z dvoch zhodných pravouhlých trojuholníkov, platí \(| \measuredangle CDA| = 180^\circ -| \measuredangle AOC| = |\measuredangle COB|\). Rovnoramenné trojuholníky \(ACD\) a BCO sú teda podobné podľa vety \(uu\). Z tejto podobnosti vyplýva rovnosť \(|CD| : |CA| = |CO| : |CB|\), takže pri zvyčajnom označení odvesien dostávame \(|CD| = \frac{1}{2}cb/a\), a z podobnosti trojuholníkov \(ACO\) a \(BCE\) potom \(|CE| = \frac{1}{2}ca/b\). Celkom tak je \[|DE| = |DC| + |CE| = \frac{cb}{2a}+\frac{ca}{2b}=\frac{cb^2 + ca^2}{2ab}= \frac{c(a^2 + b^2)}{2\cdot 2S}=\frac{c^3}{4S}.\] Poznámky. Podobnosť spomenutých rovnoramenných trojuholníkov môžeme odvodiť tiež tak, že si všimneme rovnosti zodpovedajúcich uhlov \(ACO\) a \(BCE\) pri základniach: oba totiž dopĺňajú uhol \(OCB\) do pravého uhla (\(ACB\), resp. \(OCE\)). Preto \(ACO \backsim BCE\).
Ďalšiu možnosť dáva objavenie rovnosti \(|\measuredangle ADO| = |\measuredangle BAC| = \alpha\) (ramená jedného uhla sú kolmé na ramená druhého). Z pravouhlého trojuholníka \(ODA\) tak máme \(|AO| : |AD| = \tan |\measuredangle ADO| = \tan \alpha = a : b\), takže \(|CD| = |AD| = \frac{1}{2}cb/a\), a analogicky pre pravouhlý trojuholník \(OEB\).
Úloha 64-I-6
Riešenie*
Poznámka. Za správne riešenie možno uznať aj riešenie pomocou kalkulačky. Ak majú totiž byť za desatinnou čiarkou dve deviatky, musí byť číslo \(n\) veľmi blízko zľava k nejakej druhej mocnine. Preto stačí na kalkulačke vyskúšať čísla \(\sqrt{3}, \sqrt{8}, \sqrt{15}\) atď. Keďže \(51^2= 2 601\), nájdeme, že \(\sqrt{2 600} = 50,990 195\ldots\)
Úloha 57-S-2
Riešenie*
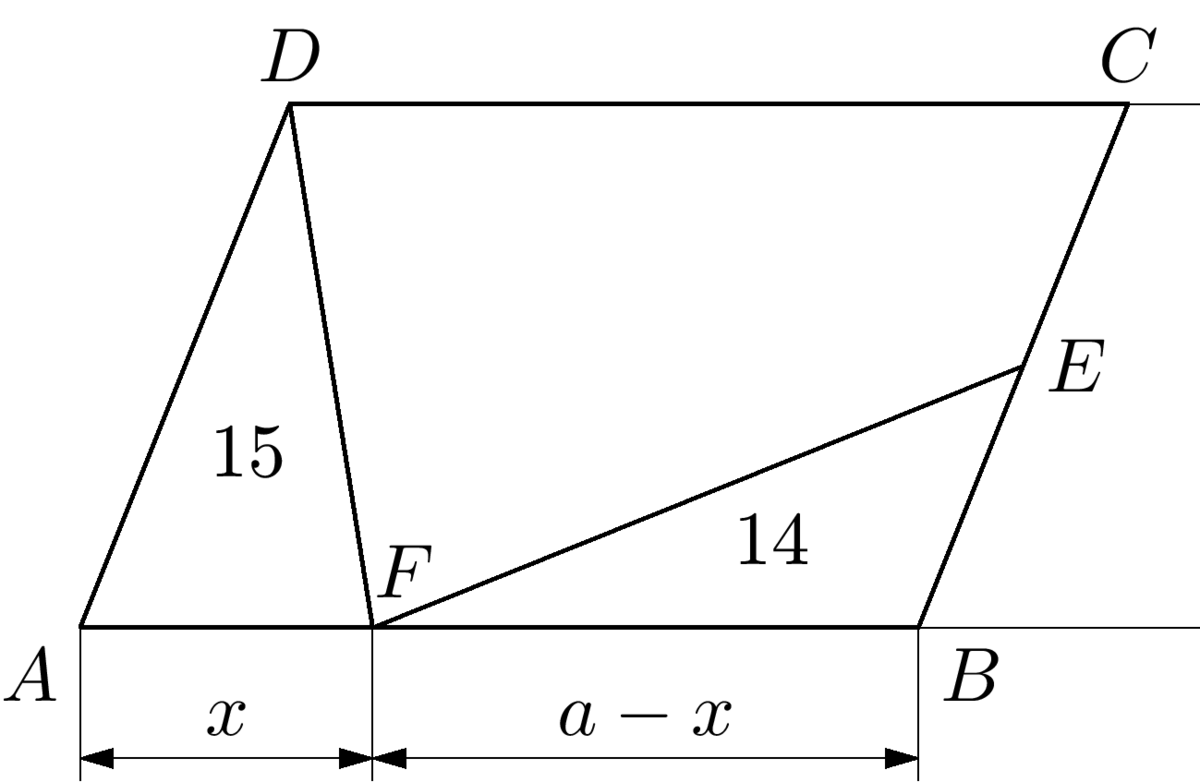
[fig:57S2_1]
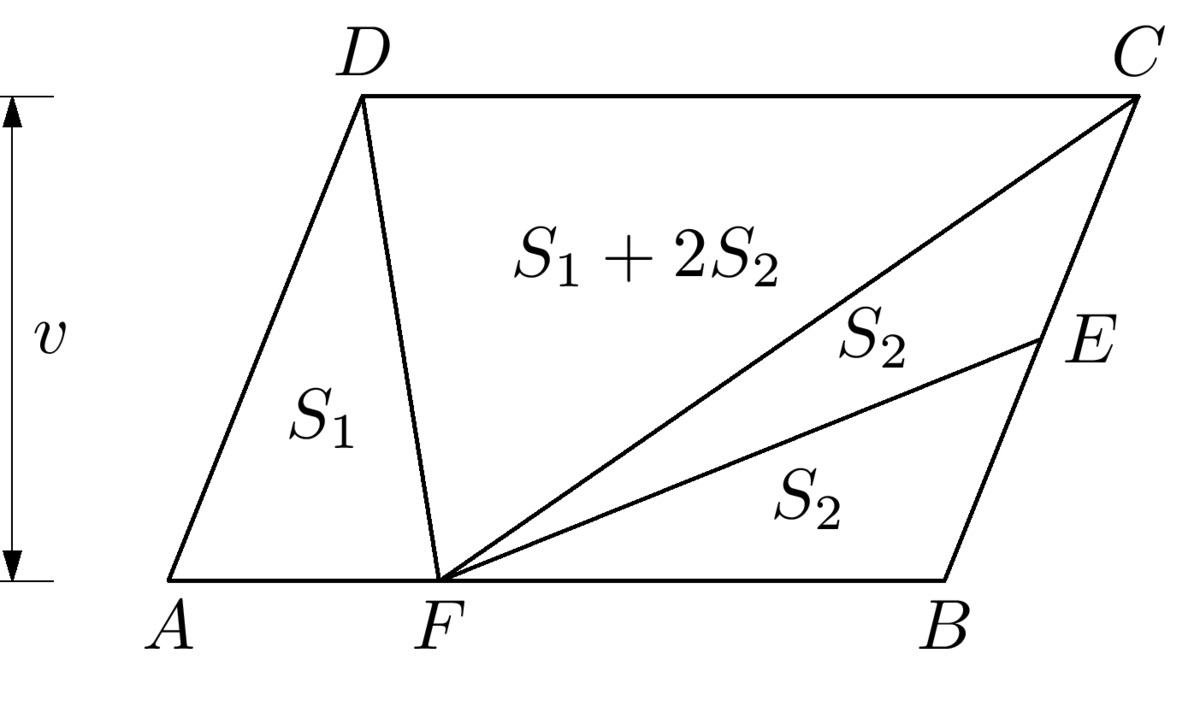
[fig:57S2_2]
Iné riešenie*. Trojuholníky \(BEF\) a \(ECF\) majú spoločnú výšku z vrcholu \(F\) a zhodné základne \(BE\) a \(EC\). Preto sú obsahy oboch trojuholníkov rovnaké. Z obr. [fig:57S2_2] vidíme, že obsah trojuholníka \(CDF\) je polovicou obsahu rovnobežníka \(ABCD\) (oba útvary majú spoločnú základňu \(CD\) a rovnakú výšku). Druhú polovicu tvorí súčet obsahov trojuholníkov \(AFD\) a \(BCF\). Odtiaľ \(S_{FECD} = S_{ECF} + S_{CDF} = S_{ECF} + (S_{AFD} + S_{BCF}) = S_{AFD} + 3 S_{FBE} = 57\) cm\(^2\).
Iné riešenie*. Do rovnobežníka dokreslíme úsečky \(FG\) a \(EH\) rovnobežné so stranami \(BC\) a \(AB\) tak, ako znázorňuje obr. [fig:58S2_3].
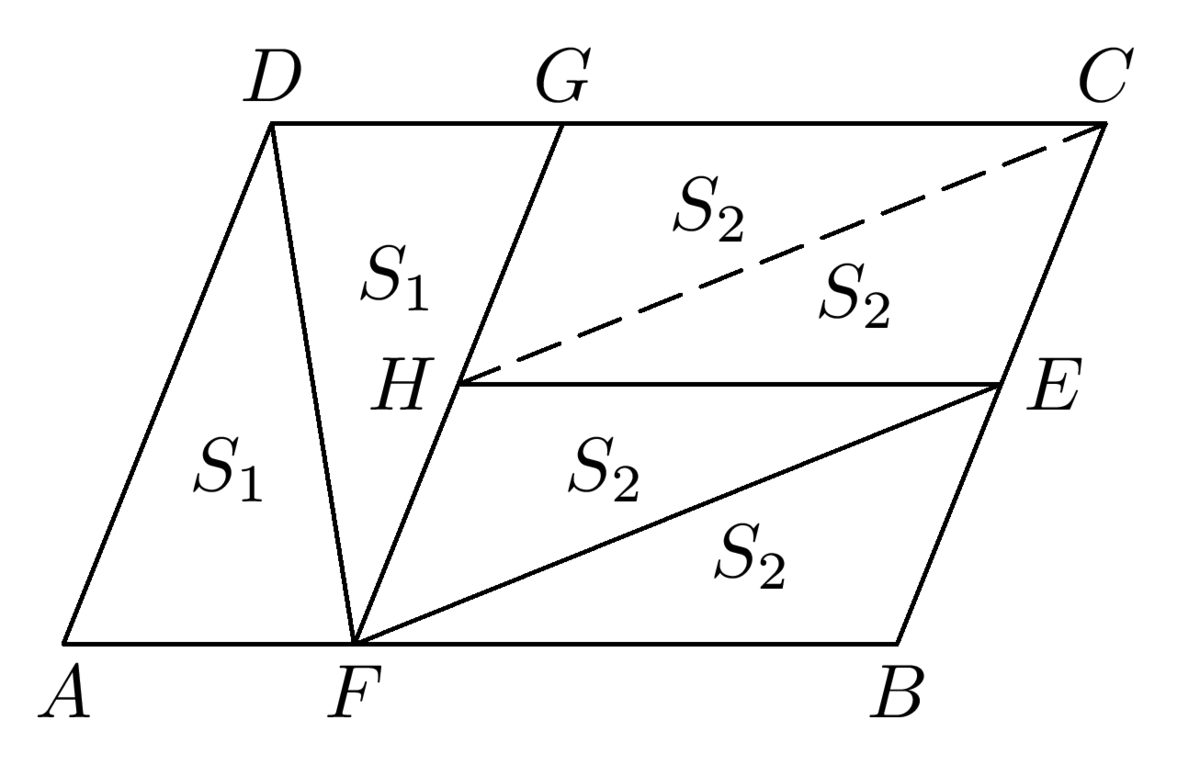
[fig:58S2_3]
Rovnobežníky \(AFGD\) a \(FBEH\) sú svojimi uhlopriečkami \(DF\) a \(EF\) rozdelené na dvojice zhodných trojuholníkov. Takže \(S_{GDF} = S_{AFD} = 15\) cm\(^2\) a \(S_{HFE} = S_{BEF} = 14\) cm\(^2\). Zo zhodnosti rovnobežníkov \(HECG\) a \(FBEH\) navyše ľahko usúdime, že všetky štyri trojuholníky \(FBE\), \(EHF\), \(HEC\) a \(CGH\) sú zhodné, takže obsah štvoruholníka \(FECD\) je \(S_{AFD} + 3S_{FBE} = 57\) cm\(^2\).
Komentár
Úloha je zaradená ako rozcvička pred komplexnejšími problémami, nie je totiž veľmi náročná na vyriešenie. Pekne tiež demonštruje, že niekedy nám vhodný prístup, náčrtok alebo správne nakreslená priamka v obrázku riešenie úlohy významne zjednoduší.Úloha 66-II-1
Riešenie*
Ak by platilo \(P(1) = 4\), bol by súčin \(P(1)\cdot P(2)\cdot P(3)\) aspoň \(4 \cdot 17 \cdot (2 \cdot 17) = 8 \cdot 17^2\), čo nevyhovuje zadaniu. Preto \(P(1) = 2\) a tak je nutne \(P(2) = 17\), pretože keby bolo \(P(2) = 4\), musel by byť daný súčin \(4 \cdot 17^2\) deliteľný číslom \(P(1)\cdot P(2) = 8\), čo neplatí, a pre \(P(2) = 2 \cdot 17\) by bol súčin \(P(1)\cdot P(2)\cdot P(3)\) opäť príliš veľký. Pre tretiu neznámu hodnotu \(P(3)\) potom vychádza \(P(3) = 4 \cdot 17^2 /(2 \cdot 17) = 2 \cdot 17\).
Hľadané koeficienty \(a\), \(b\), \(c\) tak sú práve také celé čísla, ktoré vyhovujú sústave \[\begin{aligned} P(1) &= a + b + c = 2,\\ P(2) &= 4a + 2b + c = 17,\\ P(3) &= 9a + 3b + c = 34.\end{aligned}\] Jej vyriešením dostaneme \(a = 1\), \(b = 12\), \(c = -11\).
Záver. Úlohe vyhovuje jediný mnohočlen \(P(x) = x^2 + 12x - 11\).
Komentár
Úloha spája poznatky o deliteľnosti, mnohočlenoch a na jej úspešné doriešenie je nutná aj schopnosť popasovať sa so sústavou troch rovníc s tromi neznámymi. Zaujímavé bude tiež pozorovať, koľko študentov si spomenie, že podobnou úlohou sa už zaoberali v seminári 6.Úloha 65-I-4-N1
Riešenie
Úloha 63-I-5-N2
Riešenie
Komentár
Posledná úloha zo série jednoduchých dôkazov deliteľnosti využíva podobnú myšlienku ako úloha 7.2, navyše však vyžaduje upravenie výrazu \(n^2-1\) do vhodného tvaru. Následná diskusia o riešení je už jednoduchá.Úloha 59-I-1-N3
Riešenie*
Úloha 58-I-2
Riešenie*
Výška \(v = CP\) rozdeľuje trojuholník \(ABC\) na trojuholníky \(ACP\) a \(CBP\) podobné trojuholníku \(ABC\) podľa vety \(uu\) (\(\alpha + \beta = 90^\circ\)), úsečka \(OC\) je kolmá na \(DE\) a navyše \(|OC| = |OA| = r\) (polomer opísanej kružnice). Odtiaľ \(|\measuredangle OCA| = |\measuredangle OAC| = \alpha\) a \(|\measuredangle DCA| = 90^\circ - |\measuredangle OCA| = \beta\).
Pravouhlé trojuholníky \(ACP\) a \(ACD\) so spoločnou preponou \(AC\) sa teda zhodujú aj v uhloch pri vrchole \(C\). Sú preto zhodné, dokonca súmerne združené podľa priamky \(AC\). Analogicky sú trojuholníky \(CBP\) a \(CBE\) súmerne združené podľa \(BC\). Takže \(|CD|= |CE| = v\), čiže \(|DE| = 2v = 2ab/\sqrt{a^2 + b^2}\), lebo z dvojakého vyjadrenia dvojnásobku obsahu trojuholníka \(ABC\) vyplýva \(v = ab/|AB|\), pričom \(|AB| =\sqrt{a^2 + b^2}\).
Poznámka. Namiesto dvojakého vyjadrenia obsahu môžeme na výpočet výšky \(CP\) využiť podobnosť trojuholníkov \(CBP\) a \(ABC\): \(\sin \alpha = |CP|/|AC| = |BC|/|AB|\).
[fig:58I2_1]

[fig:58I2_2]
Iné riešenie*. Úsečka \(OC\) je strednou priečkou lichobežníka \(DABE\), lebo je rovnobežná so základňami a prechádza stredom \(O\) ramena \(AB\). Preto \(D\) je obrazom bodu \(E\) v súmernosti podľa stredu \(C\). Obraz \(F\) bodu \(B\) v tej istej súmernosti leží na polpriamke \(AD\) za bodom \(D\) (obr. [fig:58I2_2]). Máme \(|CF| = |BC| = a\), uhol \(ACF\) je pravý, a teda trojuholníky \(AFC\) a \(ABC\) sú zhodné. Vidíme, že \(CD\) je výška v trojuholníku \(AFC\) zhodná s výškou \(v_c\) trojuholníka \(ABC\), a \(DE\) je jej dvojnásobkom. Veľkosť výšky \(v_c\) dopočítame rovnako ako v predchádzajúcom riešení.
Záver. \(|DE| = 2ab/\sqrt{a^2 + b^2}\).
Úloha 58-I-5-N2
Riešenie*
Úloha 64-I-4-N1
Riešenie

Trojuholníky \(ABU\) a \(CDU\) sú zrejme podobné (\(|\measuredangle BAU|=|\measuredangle UCD|\), \(|\measuredangle ABU|=|\measuredangle CDU|\), \(|\measuredangle AUB|=|\measuredangle CUD|\), pretože prvé dve sú dvojice striedavých uhlov, posledné dva sú uhly vrcholové) s koeficientom podobnosti \(k=a/c\). Preto pre výšku \(v_1\) na stranu \(AB\) v trojuholníku \(ABU\) a výšku \(v_2\) na stranu \(CD\) v trojuholníku \(CDU\) platí \(v_1/v_2=k\), resp. \(v_1=kv_2=(av_2)/c\). Potom pre pomer obsahov trojuholníkov \(ABU\) a \(CDU\) máme \[\frac{S_{ABU}}{S_{CDU}}=\frac{\frac{1}{2}av_1}{\frac{1}{2}cv_2}=\frac{a\frac{av_2}{c}}{cv_2}=\frac{a^2}{c^2}.\]
Záverečný komentár
Na prvý pohľad by sa mohlo zdať, že študenti budú o(c)hromení množstvom nových poznatkov v tomto seminári. Dúfame však, že sa tak nestane, keďže veľká väčšina obsahu by mala byť prinajmenšom povedomá, ak nie úplne zrozumiteľná. Seminár tiež patrí k tým menej náročným, avšak je veľmi dôležitou prípravou pred tvrdšími orieškami.
Úloha 58-I-4
Riešenie*
Ďalej uvažujme bod \(G\), ktorý je priesečníkom priamky \(BC\) a rovnobežky s \(AF\) prechádzajúcej bodom \(E\). Potom sú opäť obsahy trojuholníkov \(AFE\) a \(AFG\) zhodné, a sú preto zhodné aj obsahy štvoruholníka \(ABFE\) a trojuholníka \(ABG\). Bod \(G\) tak má požadovanú vlastnosť.
Hľadaný bod je na polpriamke \(BC\) jediný, lebo pre rôzne body \(X\), \(Y\) na polpriamke \(BC\) majú trojuholníky \(ABX\) a \(ABY\) rôzne výšky na spoločnú stranu \(AB\), majú teda rôzne obsahy. Popis konštrukcie.
\(p\); \(p \parallel EC, D \in p\);
\(F\); \(F \in p \cap BC\);
\(q\); \(q \parallel AF, E \in q\);
\(G\); \(G \in q \cap BC\);
Úloha má jediné riešenie.
Úloha 66-I-4
Riešenie*
Úloha 64-I-5
Riešenie*
a) \(u = 2 014\) a \(v = 1\): \(u - v~= 2 013\) nedelí 2 010;
b) \(u = 19 \cdot 53 = 1 007\) a \(v = 2\): \(u - v~= 1 005 \mid 2 010\), \(d = 2\), \(a = 1 007 \cdot 2 = 2 014\), \(b = 2 \cdot 2 = 4\);
c) \(u = 2 \cdot 53 = 106\) a \(v = 19\): \(u - v~= 87\) nedelí 2 010;
d) \(u = 53\) a \(v = 2 \cdot 19 = 38\): \(u - v= 15 \mid 2010\), \(d = 134\), \(a = 53 \cdot 134 = 7 102\), \(b = 38 \cdot 134 = 5 092\).
Záver. Hľadané čísla tvoria jednu z dvojíc \((2014, 4)\) alebo \((7 102, 5 092)\).
Komentár
Úloha neprináša žiadne nové poznatky a princípy, je však vhodná na trénovanie riešenia sústavy dvoch rovníc s dvomi neznámymi a opäť tak vytvorí prepojenie s minulými seminármi.Úloha 62-I-2-D4
Riešenie*
Úloha B-58-I-5
Riešenie*
teda zhodné. Podľa vety o obvodových uhloch sú zhodné aj uhly \(BCK\) a \(BAK\), resp.\(ACK\) a \(ABK\), preto sú zhodné aj uhly \(BCK\) a \(ACK\). Polpriamka \(CK\) je teda osou uhla \(ACB\): \[|\measuredangle ACK| = |\measuredangle BCK| = \frac{\gamma}{2}.\] Keďže bod \(P\) leží na osi strany \(AC\), je trojuholník \(ACP\) rovnoramenný a jeho vnútorné uhly pri základni \(AC\) majú veľkosť \(\frac{1}{2}\gamma\), takže jeho vonkajší uhol \(APK\) pri vrchole \(P\) má veľkosť \(\frac{1}{2}\gamma + \frac{1}{2}\gamma = \gamma\). Rovnako z rovnoramenného trojuholníka \(BCQ\) odvodíme, že aj veľkosť uhla \(BQK\) je \(\gamma\). Podľa vety o obvodových uhloch sú zhodné uhly \(ABC\) a \(AKC\), teda uhol \(AKC\) (čiže uhol \(AKP\)) má veľkosť \(\beta\) a – celkom analogicky – uhol \(BKQ\) má veľkosť \(\alpha\).
V každom z trojuholníkov \(AKP\) a \(BKQ\) už poznáme veľkosti dvoch vnútorných uhlov (\(\beta\), \(\gamma\), resp. \(\alpha\), \(\gamma\)), takže vidíme, že zostávajúce uhly \(KAP\) a \(KBQ\) majú veľkosti\(\alpha\), resp. \(\beta\).
Z predošlého vyplýva, že trojuholníky \(AKP\) a \(KBQ\) sú zhodné podľa vety \(usu\), lebo majú zhodné strany \(AK\) a \(KB\) aj obe dvojice k nim priľahlých vnútorných uhlov.
K uvedenému postupu dodajme, že výpočet uhlov \(KAP\) a \(KBQ\) cez uhly \(APK\) a \(BQK\) možno obísť takto: zhodnosť uhlov \(KAP\) a \(BAC\) (resp. \(KBQ\) a \(ABC\)) vyplýva zo zhodnosti uhlov \(KAB\) a \(PAC\) (resp. \(KBA\) a \(QBC\)).
Komentár
Posledná úloha seminára pekne kombinuje vlastnosti uhlov a zhodnosť trojuholníkov, je tak dôstojným zakončením tohto geometrického stretnutia.Úloha 60-I-5-D4
Riešenie*
Úloha B-66-II-3
Riešenie*

Vzhľadom na to, že \(CEFH\) je tetivový štvoruholník, je jeho vnútorný uhol pri vrchole \(H\) zhodný s vonkajším uhlom pri jeho protiľahlom vrchole \(E\). Platí teda \[\label{eq:B66II3_2}
|\measuredangle CHF| = |\measuredangle DEF|.\] Z rovností [eq:B66II3_1] a [eq:B66II3_2] vyplýva na základe vety \(uu\) podobnosť trojuholníkov \(DEF\) a \(CHF\). Tým je dôkaz hotový.
Komentár
Úloha je relatívne jednoduchou aplikáciou poznatkov o stredových, obvodových a úsekových uhloch, preto dobe poslúži ako úvodná úloha seminára. Zároveň sa v úlohe vyskytuje spoločná tetiva dvoch kružníc, ktorá je prvkom mnohých geometrických úloh v kategórii B, takže je príjemné, že sa študenti s týmto prípadom zoznámia hneď na začiatku.Úloha 66-S-1
Riešenie*
\(x \in (-\infty, -2)\): dostávame rovnicu \(-x - 2 = -3x + 7 - (9 - 2x)\), ktorá po úprave prejde na identitu \(0 = 0\). Všetky čísla zo skúmaného intervalu pôvodnej rovnici vyhovujú.
\(x \in \langle -2, \frac{7}{3})\): dostávame rovnicu \(x+2 = -3x+7-(9-2x)\), čiže \(2x = -4\) s jediným riešením \(x = -2\), ktoré, ako už vieme, pôvodnej rovnici nevyhovuje.
\(x \in \langle \frac{7}{3}, \frac{9}{2})\): dostávame rovnicu \(x + 2 = 3x - 7 - (9 - 2x)\) s riešením \(x = \frac{9}{2}\) , ktoré však v uvažovanom intervale neleží.
\(x \in \langle \frac{9}{2}, \infty)\): dostávame rovnicu \(x + 2 = 3x - 7 - (-9 + 2x)\), ktorá po úprave prejde na identitu \(0 = 0\). Vyhovujú všetky \(x\) z tohto intervalu.
Záver. Všetky riešenia úlohy tvoria množinu \((-\infty, -2) \cup \langle \frac{9}{2},\infty)\).
Úloha 59-I-1-D1
Riešenie*
Úloha B-60-I-1-N2
Riešenie*
Úloha 62-I-1-N2
Riešenie*
Komentár
Ako sme už spomínali, táto úloha je tiež prípravou na domácu prácu. Je tiež vhodným miestom, kde môžeme prípadným tápajúcim študentom pripomenúť metódu riešenia, s ktorou sme sa už stretli: pokúsiť sa vypozorovať, ako sa úloha správa pre menšie rozmery, napr. tabuľku \(3\times 3\) a potom objavené výsledky zovšeobecniť.Úloha 64-I-4
Riešenie*
Trojuholníky \(ABG\) a \(CDG\) sú podobné, preto \((x + y) : z~= 6 : 2 = 3 : 1\). Aj trojuholníky \(AEF\) a \(CDF\) sú podobné, preto \(x : (y + z) = 3 : 2\).

Odvodené úmery zapíšeme ako sústavu rovníc \[\begin{aligned}
x + y - 3z &= 0,\\
2x - 3y - 3z &= 0.\end{aligned}\] Ich odčítaním získame rovnosť \(x = 4y\), čiže \(x : y = 4 : 1\). Dosadením tohto výsledku do prvej rovnice dostaneme \(5y = 3z\), čiže \(y : z~= 3 : 5\). Spojením oboch pomerov získame výsledok \(x : y : z~= 12 : 3 : 5\).
Komentár
Úloha je výborným tréningom na hľadanie vhodných dvojíc podobných trojuholníkov tak, aby sme pomocou údajov zo zadania boli schopní určiť hľadaný pomer, keďže jedna dvojica trojuholníkov na nájdenie odpovede zjavne stačiť nebude. Okrem toho tiež pozorovania z náčrtu vedú k sústave dvoch rovníc, takže študenti uplatnia aj svoje algebraické zručnosti.Úloha 62-II-2
Riešenie*

Trojuholníky \(ABL\) a \(DCL\) majú zhodné strany \(AB\) a \(CD\). Ak \(v_3\) označuje príslušnú výšku druhého z nich, je výška prvého z nich rovná \(v + v_3\), takže pre rozdiel obsahov týchto trojuholníkov platí \[\begin{aligned}
S_{ABL} - S_{DCL} &= \frac{1}{2} |AB| \cdot (v~+ v_3 ) - \frac{1}{2}|CD|\cdot v_3 =\frac{1}{2} |AB| \cdot (v~+ v_3 - v_3 ) =\\
&= \frac{1}{2} |AB| \cdot v~= \frac{1}{2} S_{ABCD} = S_{BCK} + S_{DAK}.\end{aligned}\] Odtiaľ vyplýva \[S_{ABL} = S_{BCK} + S_{DAK} + S_{DCL} = 60\,\text{cm}^2.\]
Komentár
Úloha precvičuje použitie tvrdenia, ktoré sme dokázali v prvom geometrickom seminári, a to, že ak majú dva trojuholníky základňu rovnakej dĺžky, potom ich obsahy sú v rovnakom pomere ako ich výšky na túto základňu.Úloha 61-I-6-N1
Riešenie*
Komentár
Úloha je netriviálna, jej zvládnutie je však výborným predpokladom na úspešné vyriešenie domácej práce. Ak nám ostane na konci seminára dostatok času, môžeme študentov najprv odohrať pár kôl hry pre nimi zvolené rozmery tabuľky a na základe poznatkov z hry potom presne popísať víťaznú stratégiu.Úloha 63-I-4-N2
Riešenie*
Úloha 66-I-6-N1
Riešenie*
Úloha 66-II-2
Uveďte príklad takého zaplnenia tabuľky, že súčet každých dvoch čísel v rovnakom riadku či v rovnakom stĺpci je väčší ako 11.
Dokážte, že pri ľubovoľnom zaplnení tabuľky sa v niektorom riadku alebo stĺpci nájdu dve čísla, ktorých súčet neprevyšuje 12.
Riešenie*
| 1 | 35 | 33 | 29 | 25 | 19 |
|---|---|---|---|---|---|
| 36 | 2 | 30 | 26 | 20 | 15 |
| 34 | 31 | 3 | 21 | 16 | 11 |
| 32 | 27 | 22 | 4 | 12 | 9 |
| 28 | 23 | 17 | 13 | 5 | 7 |
| 24 | 18 | 14 | 10 | 8 | 6 |
Najmenšie súčty dvoch čísel z jednotlivých riadkov (zhora nadol) sú \[1 + 19, 2 + 15, 3 + 11, 4 + 9, 5 + 7, 6 + 8\] a z jednotlivých stĺpcov (zľava doprava) \[1 + 24, 2 + 18, 3 + 14, 4 + 10, 5 + 8, 6 + 7.\] Rýchlejší opis príkladu vyhovujúcej tabuľky a jeho jednoduchšiu kontrolu dostaneme, keď do tabuľky vpíšeme iba čísla od 1 do 12, ako vidíme nižšie. Rozmiestnenie čísel od 13 do 36 do prázdnych políčok už zrejme môže byť ľubovoľné – dve najmenšie čísla v každom riadku aj stĺpci sú totiž práve tie od 1 do 12.
| 1 | 11 | ||||
|---|---|---|---|---|---|
| 12 | 2 | ||||
| 3 | 9 | ||||
| 10 | 4 | ||||
| 5 | 7 | ||||
| 8 | 6 |
b) Ak sú dve z čísel od 1 do 6 v rovnakom riadku alebo v rovnakom stĺpci, ich súčet neprevýši dokonca ani číslo \(6 + 5 = 11\). V opačnom prípade sú čísla od 1 do 6 rozmiestnené vo všetkých riadkoch a všetkých stĺpcoch, takže číslo 7 je v rovnakom riadku s číslom \(x\) a v rovnakom stĺpci s číslom \(y\), pričom \(x\) a \(y\) sú dve rôzne čísla od 1 do 6. Potom menšie z čísel \(7 + x\) a \(7 + y\) neprevýši menšie z čísel \(7 + 6\) a \(7 + 5\), teda číslo 12. Tým je tvrdenie dokázané.
Komentár
Úloha je relatívne jednoduchá a nevyžaduje žiadne špeciálne matematické vedomosti, len starostlivý logický úsudok. Študenti pravdepodobne vymyslia rôzne zaplnenia tabuľky a to môže byť výbornou príležitosťou nechať ich riešenia skontrolovať si medzi sebou navzájom.Úloha B-66-I-5-D1
Riešenie*
Úloha 62-I-4-D1
Riešenie*
Úloha 60-S-3
Riešenie*
Iné riešenie*. Vieme, že \(60 = 3 \cdot 4 \cdot 5\). Pritom čísla 3, 4, 5 sú po dvoch nesúdeliteľné, preto na dôkaz deliteľnosti 60 stačí dokázať deliteľnosť jednotlivými číslami 3, 4, 5.
Keďže číslo \(3x + 5y\) je deliteľné \(5\), je aj \(x\) deliteľné 5. Podobne z relácie \(5 \mid 5x + 2y\) vyplýva \(5 \mid y\). Preto 5 delí aj \(2x + 3y\).
Keďže číslo \(3x + 5y\) je deliteľné 3, je \(y\) deliteľné 3. Vzhľadom na \(3 \mid 5x + 2y\) máme tiež \(3 \mid 5x\), a teda \(3 \mid x\). Preto 3 delí aj \(2x + 3y\).
Keďže \(4 \mid 3x + 5y\) a \(4 \mid 5x + 2y\), máme aj \(4 \mid (3x + 5y) + (5x + 2y) = 8x + 7y\), takže \(4 | y\). Ďalej napríklad \(4 \mid 3x + 5y\), takže \(4 \mid 3x\), čiže \(4 \mid x\). Preto 4 delí aj \(2x + 3y\).
Iné riešenie*.. Vyjadríme výraz \(2x + 3y\) pomocou \(3x + 5y\) a \(5x + 2y\). Budeme hľadať čísla \(p\) a \(q\) také, že \(2x + 3y = p(3x + 5y) + q(5x + 2y)\) pre každú dvojicu celých čísel \(x\), \(y\). Jednoduchou úpravou dostaneme rovnicu \[(2 - 3p - 5q)x + (3 - 5p - 2q)y = 0. \ \ \ \todo{(1)}\] Ak budú hľadané čísla \(p\) a \(q\) spĺňať sústavu \[\begin{aligned} 3p + 5q &= 2,\\ 5p + 2q &= 3,\end{aligned}\] bude zrejme rovnosť splnená pre každú dvojicu \(x\), \(y\). Vyriešením sústavy dostaneme \(p = 11/19\), \(q = 1/19\). Dosadením do dostávame vyjadrenie \[19(2x + 3y) = 11(3x + 5y) + (5x + 2y),\] z ktorého vyplýva, že spolu s číslami \(3x + 5y\) a \(5x + 2y\) je súčasne deliteľné 60 aj číslo \(2x + 3y\), pretože čísla 19 a 60 sú nesúdeliteľné.
Úloha 63-I-5-N5
Riešenie*
Úloha 63-I-4
Riešenie*

Komentár
Opäť je potrebné identifikovať podobné trojuholníky a potom pomocou známeho koeficientu určiť ich obsahy. Oproti predchádzajúcej úlohe ešte študenti navyše využijú Pytagorovu vetu.Úloha B-66-I-5-N3
Riešenie*
Úloha 57-I-2-N3
Riešenie*
Úloha 57-I-4-D1
Riešenie*
Úloha 59-I-2
Riešenie*
Zvoľme teraz ľubovoľnú priamku \(q\) tak, aby mala s pravouholníkom \(ABCD\) spoločný iba bod \(C\). Jej priesečníky s priamkami \(AB\), \(AD\) označme \(M\) a \(N\) (v uvedenom poradí). Ďalej označme \(M'\) obraz bodu \(M\) v osovej súmernosti podľa priamky \(BC\) a \(N*\) obraz bodu \(N\) v osovej súmernosti podľa priamky \(CD\). Keďže \(|\measuredangle NCD| + |\measuredangle MCB|= 180^\circ- |\measuredangle BCD| = 90^\circ\), vyplýva z práve uvedených súmerností rovnosť \(|\measuredangle MCM'| = 2|\measuredangle MCB| = 2(90^\circ - |\measuredangle NCD|) = 180^\circ - 2|\measuredangle NCD| = 180^\circ - |\measuredangle NCN* |\). Body \(C\), \(M'\) a \(N*\) teda ležia na jednej polpriamke s počiatkom \(C\). Pre obsah trojuholníka \(AMN\) tak vždy platí () \[S_{AMN}= S_{ABCD} + S_{BMC} + S_{DCN} = S_{ABCD} + S_{M'BC} + S_{DN*C} \geq 2S_{ABCD},\] s rovnosťou práve vtedy, keď polpriamka \(CM'= CN*\) bude prechádzať vrcholom \(A\) daného pravouholníka, t. j. práve vtedy, keď \(M'= A = N*\) (potom budú \(BC\) a \(CD\) strednými priečkami trojuholníka \(AMN\)).
Záver. Priamku \(q\), pre ktorú je obsah trojuholníka \(AMN\) minimálny, zostrojíme ako priamku \(CM\), pričom \(M\) je obraz bodu \(A\) v osovej súmernosti podľa osi \(BC\). Priamka \(p\) s najväčšou možnou vzdialenosťou od bodu \(A\) pri daných podmienkach je kolmica na úsečku \(AC\) zostrojená v bode \(C\)
Poznámka. K práve uvedenému riešeniu môže žiakov inšpirovať aktivita so sklada- ním papiera opísaná v úlohe N1. Namiesto skladania papiera možno situáciu modelovať na počítači v niektorom z nástrojov dynamickej geometrie, napríklad v Cabri geometrii alebo v Geonexte.
Iné riešenie*. Označme \(P\) pätu kolmice z bodu \(A\) na hľadanú priamku \(p\) a \(\varphi\) veľkosť odchýlky priamok \(p\) a \(AC\). Pre vzdialenosť \(d\) priamky \(p\) od bodu \(A\) platí \(d = |AP| = |AC| \sin \varphi \leq |AC|\). Priamka \(p\) má teda najväčšiu možnú vzdialenosť od bodu \(A\) práve vtedy, keď je kolmá na \(AC\).
Uvažujme ľubovoľnú priamku \(q\), ktorá má s pravouholníkom \(ABCD\) spoločný iba bod \(C\), a budeme hľadať, za akých podmienok ohraničuje spolu s priamkami \(AB\) a \(AD\) trojuholník s najmenším obsahom. Použijeme označenie z a označíme \(a = |AB| = |DC|\), \(x = |BM|\), \(b = |AD| = |BC|\) a \(y = |DN|\). Pomocou týchto veličín vyjadríme obsah trojuholníka \(AMN\) a odhadneme ho použitím AG-nerovnosti: \[S_{AMN}=\frac{1}{2}(a + x)(b + y) = \frac{1}{2}(ab + xy + ay + bx)\geq \frac{1}{2}(ab + xy + 2\sqrt{ab \cdot xy}. \todo{(1)}\] Z podobnosti trojuholníkov \(BMC\) a \(DCN\) dostávame \(|DN|/|BC| = |DC|/|BM|\), čo vzhľadom na zvolené označenie dáva \(xy = ab\). Po dosadení do a po jednoduchej úprave tak dostaneme \(S_{AMN} = 2ab = 2S_{ABCD}\). Pritom rovnosť nastane práve vtedy, keď platí \(ay = bx\). Spolu s podmienkou \(xy = ab\) predstavujú oba vzťahy sústavu rovníc s neznámymi \(x\), \(y\), ktorej vyriešením dostaneme \(x = a\) a \(y = b\). Dospeli sme teda k rovnakému výsledku ako v prvom riešení, kde sme tiež uviedli konštrukciu priamky \(q\).
Iné riešenie*. Postupujeme rovnako ako v predchádzajúcom riešení s tým rozdielom, že najskôr z podobnosti trojuholníkov \(BMC\) a \(DCN\) určíme \(y = ab/x\) a potom odhadneme obsah trojuholníka \(AMN\) pomocou tvrdenia z úlohy takto: \[S_{AMN} =\frac{1}{2}(a + x)(b + y) =\frac{1}{2}(a + x)\bigg(b +\frac{ab}{x}\bigg)=\frac{1}{2}\bigg(2ab + bx + \frac{a^2 b}{x}\bigg)= ab +\frac{1}{2}ab\bigg(\frac{x}{a}+\frac{a}{x}\bigg)\geq 2ab.\] Rovnosť nastáva práve vtedy, keď \(x/a = a/x\), čo je ekvivalentné s podmienkou \(x = a\).
Úloha 63-I-4-N1
Určte dĺžky strán trojuholníka \(ABC\).
Dokážte, že trojuholníky \(DBF\), \(ABC\) a \(BEF\) sú navzájom podobné.
Určte dĺžky strán trojuholníkov \(DBF\) a \(BEF\).
Určte obsahy trojuholníkov \(ABC\), \(DBF\) a \(BEF\).
Určte obsah štvoruholníka \(AFDC\).
Riešenie*
10, 30, \(10\sqrt{10}\)
10, \(3\sqrt{10}\), \(\sqrt{10}\); 30, \(9\sqrt{10}\), \(3\sqrt{10}\)
150, 15, 135
135
Úloha 63-I-1-N6
Riešenie*
Úloha 61-I-5-N1
Riešenie*

Úloha 62-I-6
Riešenie*
[fig:62I6_1]

[fig:62I6_2]
Ako určiť zvyšné dva obsahy \(S_{CDM}\) a \(S_{FAM}\), keď zatiaľ poznáme len ich súčet \(S/3\)? Všimnime si, že súčet zadaných obsahov trojuholníkov \(ABM\) a \(BCM\) má významnú hodnotu \(S/6\), ktorá je aj obsahom trojuholníka \(ABC\) (to vyplýva opäť z obr. [fig:62I6_2]). Taká zhoda obsahov znamená práve to, že bod \(M\) leží na uhlopriečke \(AC\). Trojuholníky \(ABM\) a \(BCM\) tak majú zhodné výšky zo spoločného vrcholu \(B\) a to isté platí aj pre výšky trojuholníkov \(CDM\) a \(FAM\) z vrcholov \(F\) a \(D\) (t. j. bodov, ktoré majú od priamky \(AC\) rovnakú vzdialenosť). Pre pomery obsahov týchto dvojíc trojuholníkov tak dostávame \[\frac{S_{CDM}}{S_{FAM}}=\frac{|CM|}{|AM|}=\frac{S_{BCM}}{S_{ABM}}=\frac{2}{3}.\] V súčte \(S_{CDM} + S_{FAM}\) majúcom hodnotu \(S/3\) sú teda sčítance v pomere \(2 : 3\). Preto \(S_{CDM} =4\) cm\(^2\) a \(S_{FAM} = 6\) cm\(^2\).
Komentár
Úloha je odľahčeným a netradičným príkladom využitia princípu, na ktorom sme stavali celé toto seminárne stretnutie: súčty obsahov trojuholníkov sú stále rovnaké. Posledná časť úlohy vyžaduje netriviálny nápad a študenti tak možno budú potrebovať malú radu.Úloha 59-I-1-D2
Riešenie*
Úloha 65-I-4-D2
Riešenie*
Úloha 58-II-2
Riešenie*
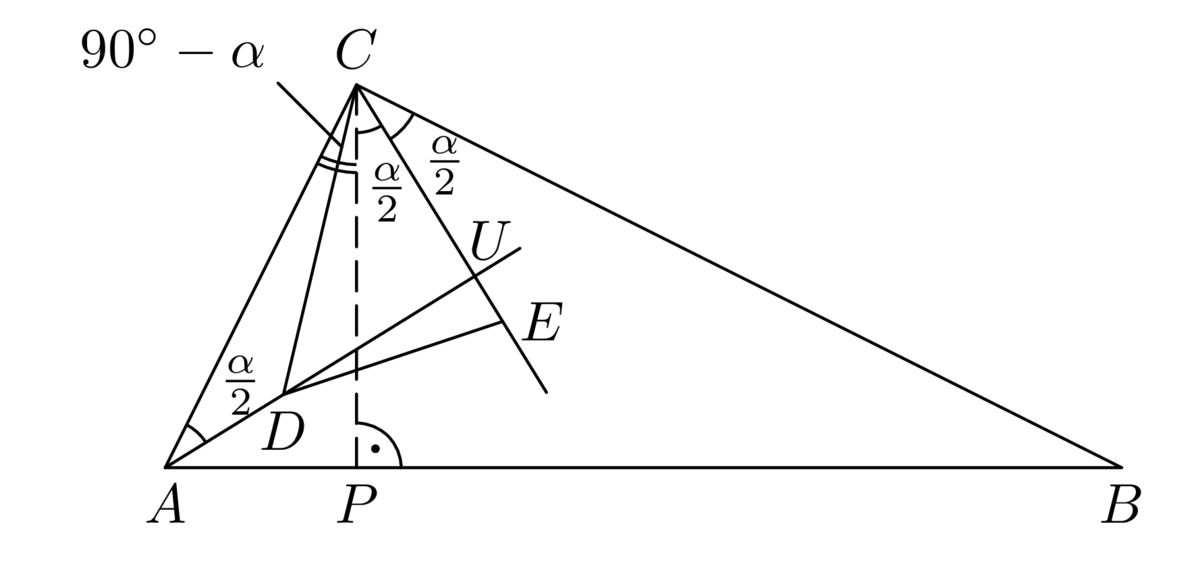
[fig:58II2_1]
Iné riešenie*. Označme \(F\) a \(G\) zodpovedajúce priesečníky priamok \(CD\) a \(CE\) so stranou \(AB\) (obr. [fig:58II2_2]). Podľa úlohy vyriešenej na seminári v škole je trojuholník \(CAG\)
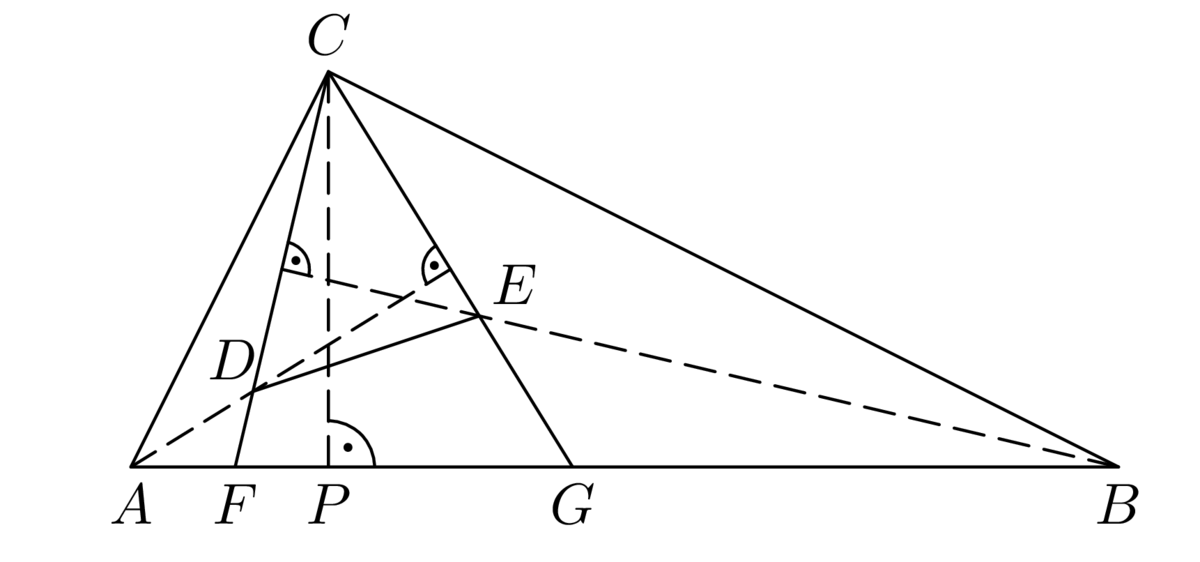
[fig:58II2_2]
rovnoramenný so základňou \(CG\). Os \(AD\) uhla \(CAG\) rovnoramenného trojuholníka \(CAG\) je tak aj jeho osou súmernosti, a je preto kolmá na základňu \(CG\), teda aj na \(CE\). Podobne zistíme, že aj trojuholník \(CBF\) je rovnoramenný so základňou \(CF\), takže os \(BE\) uhla \(FBC\) je kolmá na \(CF\), teda aj na \(CD\). Priesečník oboch osí \(AD\) a \(BE\) je tak nielen stredom kružnice vpísanej trojuholníku \(ABC\), ale aj priesečníkom výšok trojuholníka \(CDE\), čo sme mali dokázať.
Úloha 66-I-1-N2
Riešenie*
Komentár
Úloha využíva rovnaký princíp ako prechádzajúce dve. Prvýkrát však pri úprave využívame násobenie a delenie výrazmi. Tým sa z úlohy stáva dobrá príležitosť na pripomenutie faktu, že pri úprave nerovností musíme brať do úvahy (ne)zápornosť výrazov, ktoré pri takýchto úkonoch využívame.Komentár
Ďalším z užitočných nástrojov pri dokazovaní nerovností je znalosť nerovnosti \(u+\frac{1}{u}\geq 2\) pre každé kladné reálne číslo \(u\), pričom táto nerovnosť prechádza v rovnosť len pre \(u=1\). Dokázanie tohto faktu nie je zložité: vynásobením celej nerovnosti \(u\), prevedením všetkých členov na jednu stranu dostávame \((u-1)^2\geq 0\), čo je pravdivé tvrdenie. Nasledujúce úlohy sú zaradené ako tréning uplatnenia tejto nerovnosti.Úloha 64-II-1
Určte tieto tri súčiny, ak viete, že dva z nich sa rovnajú a sú menšie ako tretí súčin.
Predpokladajme, že jeden z troch súčinov, ktorý označíme \(S\), je menší ako dva ostatné súčiny (ktoré môžu byť rovnaké). Nájdite najväčšiu možnú hodnotu \(S\).
Riešenie*
a) Označme dva z uvažovaných (rôznych) súčinov \(S\) a \(Q\), pričom \(S < Q\). Z rovnosti \[S \cdot S~\cdot Q = 2^7 \cdot 3^4 \cdot 5 \cdot 7\] vidíme, že prvočísla 5 a 7 musia byť zastúpené v súčine \(Q\), takže \(Q = 5 \cdot 7 \cdot x = 35x\), pričom \(x\) je jedno zo zvyšných čísel 1, 2, 3, 4, 6, 8 a 9. Ďalej vidíme, že v rozklade dotyčného \(x\) musí mať prvočíslo 2 nepárny exponent a prvočíslo 3 párny exponent – tomu vyhovujú iba čísla 2 a 8. Pre \(x = 2\) ale vychádza \(Q = 35 \cdot 2 = 70 < S= 2^3 \cdot 3^2 = 72\), čo odporuje predpokladu \(S < Q\). Preto je nutne \(x = 8\), pre ktoré vychádza \(Q = 35 \cdot 2 = 280\) a \(S^2 = 2^4 \cdot 3^4\) čiže \(S = 2^2 \cdot 3^2 = 36\). Trojica súčinov je teda \((36, 36, 280)\).
Ostáva ukázať, že získanej trojici naozaj zodpovedá rozdelenie daných deviatich čísel na trojice: \[S = 1 \cdot 4 \cdot 9 = 36, \ \ \ S~= 2 \cdot 3 \cdot 6 = 36, \ \ \ Q = 5 \cdot 7 \cdot 8 = 280.\]
b) Označme uvažované súčiny \(S, Q\) a \(R\), pričom \(S < Q\) a \(S < R\) (nie je ale vylúčené, že \(Q = R\)). V riešení časti a) sme zistili, že platí rovnosť \[S \cdot Q \cdot R = 70 \cdot 72 \cdot 72.\] Ak teda ukážeme, že existuje rozdelenie čísel, pri ktorom \(S = 70\) a \(R = Q = 72\), bude \(S = 70\) hľadaná najväčšia hodnota, lebo keby pri niektorom rozdelení platilo \(S \geq 71\), muselo by byť \(R \geq 72\) aj \(Q \geq 72\) a tiež \(S \cdot Q \cdot R \geq 71 \cdot 72 \cdot 72\), čo zrejme odporuje predchádzajúcej rovnosti. Nájsť potrebné rozdelenie je jednoduché: \[S~= 2 \cdot 5 \cdot 7 = 70, \ \ \ Q = 1 \cdot 8 \cdot 9 = 72, \ \ \ R = 3 \cdot 4 \cdot 6 = 72.\]
Komentár
Zaujímavá úloha, ktorá dôvtipne využíva rozklady čísel na súčin prvočísel.Úloha 59-I-2-N1
aby jeho strany \(AB\) a \(AD\) splývali s okrajom papiera. Potom zostrojte priamku, aby mala s pravouholníkom spoločný len bod \(C\) a jej prienik s hárkom papiera tvoril úsečku \(MN\), pozdĺž ktorej papier rozstrihnite. Vzniknutý papierový model trojuholníka \(AMN\) s narysovaným obdĺžnikom \(ABCD\) preložte pozdĺž úsečiek \(BC\) a \(DC\). Túto činnosť niekoľkokrát opakujte, pritom pre rovnaký pravouholník \(ABCD\) voľte rôzne dĺžky úsečky \(BM\). Čo možno z výsledku usúdiť o pomere obsahov trojuholníka \(AMN\) a pravouholníka \(ABCD\)? Hypotézu dokážte.
Riešenie
Úloha B-59-II-3
Riešenie*
Iné riešenie*. Budeme postupovať rovnako ako v druhom riešení tretej úlohy domáceho kola (je možné odvolať sa na domáce kolo bez dôkazu): Keďže \(ABLD\) je tetivový (a teda rovnoramenný) lichobežník, je \(|KD| = |BL| = |AD|\). Podobne je aj lichobežník \(KLDM\) rovnoramenný, takže \(|MK| = |DL|\) a \(|DB| = 2|MK| = 2|DL| = |DC| = |AB|\). Z podobnosti rovnoramenných trojuholníkov \(AKD\) a \(DAB\) (zhodujú sa v uhle pri vrchole \(A\) svojich základní) potom vyplýva, že \(|AK|/|AD| = |DA|/|AB|\), odkiaľ po dosadení \(|AK| = \frac{1}{2}|AB|\) vychádza \(|DB| = |AB| =\sqrt{2}\cdot|AD|\). Ďalej využijeme známu rovnobežníkovú rovnosť \(|AC|^2 + |BD|^2 = 2 \cdot |AB|^2 + 2 \cdot |AD|^2\). Dosadením dostaneme \(|AC|^2 + 2 \cdot |AD|^2 = 4 \cdot |AD|^2 + 2 \cdot |AD|^2\) a odtiaľ \(|AC|^2 = 4 \cdot |AD|^2\) čiže \(|AC| = 2 \cdot |AD|\).
Úloha 58-I-6-D1
Riešenie*
Úloha 61-I-5-N2
Riešenie*
Úloha 59-I-6
Riešenie*
a) Predpokladajme najskôr, že nuly sú na treťom a druhom mieste sprava. Hľadané číslo \(x\) má potom tvar \(x = 1 000a + b\), pričom \(a\) je prirodzené číslo (rovnako to bude aj v ďalších prípadoch, keď už to nebudeme pripomínať) a \(b\) nenulová cifra. Podmienku zo zadania \(1 000a + b = 89(10a + b)\) upravíme na tvar \(5a = 4b\), z ktorého vyplýva, že \(b\) je násobok piatich. Vyhovuje tak iba \(b = 5\) a \(a = 4\), teda \(x = 4 005\).
b) Ak hľadané číslo \(x\) má nuly na štvrtom a treťom mieste sprava, je \(x = 10 000a+b\), pričom \(b\) je dvojciferné číslo. Podmienku zo zadania \(10 000a+b = 89(100a+b)\) upravíme na tvar \(25a = 2b\), z ktorého vyplýva, že \(b\) je nepárny násobok čísla 25 (pripomíname, že \(x\), a teda ani \(b\), nie je deliteľné desiatimi). Odtiaľ \(b = 25\), \(a = 2\) alebo \(b = 75\), \(a = 6\), teda \(x \in \{20 025, 60 075\}\).
c) Ak hľadané číslo \(x\) má nuly na piatom a štvrtom mieste sprava, je \(x = 100 000a+ b\), pričom \(b\) je trojciferné číslo. Podmienku zo zadania \(100 000a + b = 89(1 000a + b)\) upravíme na tvar \(125a = b\), z ktorého vyplýva, že \(b\) je nepárny násobok čísla 125. Vyhovuje iba \(b = 125\) a \(a = 1\), \(b = 375\) a \(a = 3\), \(b = 625\) a \(a = 5\), \(b = 875\) a \(a = 7\), teda \(x \in \{100 125, 300 375, 500 625, 700 875\}\).
d) Z predošlých prípadov vidíme, že pre hľadané číslo \(x\) tvaru \(x = 10^{n+2} a + b\), pričom \(b\) je \(n\)-ciferné číslo, dostávame podmienku \(10^{n+2} a + b = 89(10^n a + b)\), čiže \(11 \cdot 10^n a = 88b\), odkiaľ pre \(n \geq 4\) dostávame podmienku \(125 \cdot 10^{n-3} a = b\), podľa ktorej je \(b\) násobkom desiatich. Žiadne ďalšie \(x\), ktoré by vyhovovalo zadaniu, teda neexistuje.
Záver. Hľadané čísla sú \(4 005, 20 025, 60 075, 100 125, 300 375, 500 625\), a \(700 875\).
Úloha 65-I-4
Ukážte, že pomer obsahov trojuholníkov \(ABC\) a \(ABD\) je pre \(p = 2 : 3\) rovnaký ako pre \(p = 3 : 2\).
Zdôvodnite, prečo pomer obsahov trojuholníkov \(ABC\) a \(ABD\) má hodnotu aspoň 4.
Riešenie*

pomer dĺžok úsečiek \(BC\) a \(ED\), a to na základe podobnosti pravouhlých trojuholníkov \(BCC_0\) a \(EDD_0\) podľa vety \(uu\) (uplatnenej vďaka \(BC \parallel ED\)).1 Platí teda rovnosť \[\label{eq:65I4_2} \frac{S_{ABC}}{S_{ABD}} =\frac{|BC|}{|ED|}.\] Vráťme sa teraz k rovnostiam [eq:65I4_1], podľa ktorých \[|EF| = (1 + p)|DF| \ \ \ \ \text{a} \ \ \ \ |AB| = (1 + p)|EA|,\] a všimnime si, že trojuholníky \(ABC\) a \(AEF\) majú spoločný uhol pri vrchole \(A\) a zhodné uhly pri vrcholoch \(C\) a \(F\) (pretože \(BC \parallel EF\)), takže sú podľa vety \(uu\) podobné. Preto pre dĺžky ich strán platí \[\frac{|AB|}{|AE|}=\frac{|BC|}{|EF|},\ \ \ \ \text{čiže} \ \ \ \ 1 + p =\frac{|BC|}{(1 + p)|DF|}, \ \ \ \ \text{odkiaľ} \ \ \ \ |BC| = (1 + p)^2 |DF|.\] Keď vydelíme posledný vzťah hodnotou \(|ED|\), ktorá je rovná \(p|DF|\) podľa [eq:65I4_1], získame podiel z pravej strany [eq:65I4_2] a tým aj hľadané vyjadrenie \[\label{eq:65I4_3} \frac{S_{ABC}}{S_{ABD}}=\frac{(1 + p)^2}{p}.\]
a) Algebraickou úpravou zlomku zo vzťahu [eq:65I4_3] \[\frac{(1 + p)^2}{p}=\frac{1 + 2p + p^2}{p}= 2 + p + \frac{1}{p}\] zisťujeme, že hodnota pomeru \(S_{ABC} : S_{ABD}\) je pre akékoľvek dve navzájom prevrátené hodnoty \(p\) a \(1/p\) rovnaká, teda nielen pre hodnoty \(2/3\) a \(3/2\), ako sme mali ukázať.
b) Podľa vzťahu [eq:65I4_3] je našou úlohou overiť pre každé \(p > 0\) nerovnosť \[\frac{(1 + p)^2}{p}\geq 4,\ \ \ \ \text{čiže} \ \ \ \ (1 + p)^2\geq 4p.\] To je však zrejme ekvivalentné s nerovnosťou \((1 -p)^2\geq 0\), ktorá skutočne platí, nech je základ druhej mocniny akýkoľvek (rovnosť nastane jedine pre \(p = 1\)).
V prípade pravých uhlov \(ABC\) a \(AED\) to platí triviálne, lebo vtedy \(B = C_0\) a \(E = D_0\).↩︎
Úloha 63-I-2-N1
Riešenie
Úloha 64-II-3
Nájdite bod \(P\) vnútri lichobežníka tak, aby obsahy trojuholníkov \(ABP\) a \(CDP\) boli v pomere \(3 : 1\) a aj obsahy trojuholníkov \(BCP\) a \(DAP\) boli v pomere \(3 : 1\).
Pre nájdený bod \(P\) určte postupný pomer obsahov trojuholníkov \(ABP\), \(BCP\), \(CDP\) a \(DAP\).
Riešenie*
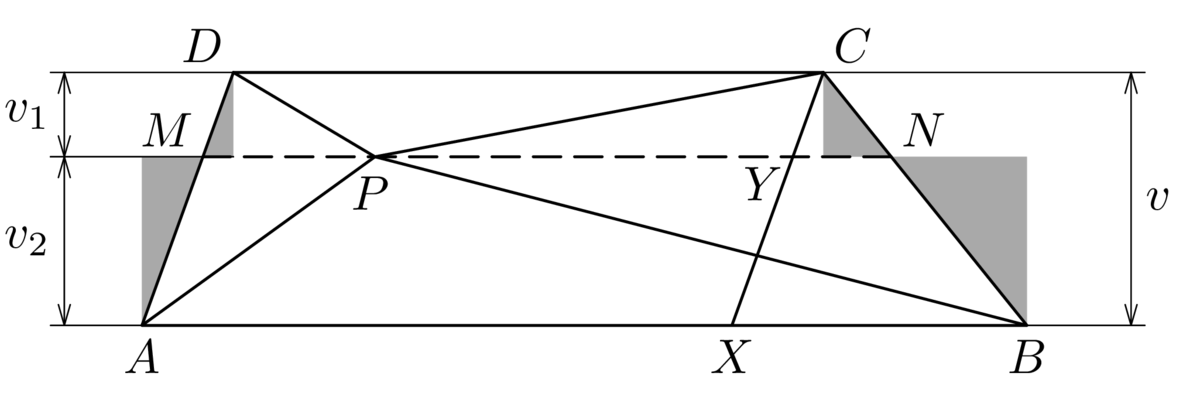
a) Keďže obsahy trojuholníkov \(ABP\) a \(CDP\) sú v pomere \(3 : 1\), platí \[\frac{|AB|v_2}{2}:\frac{|CD|v_1}{2}= 3 : 1, \ \ \ \ \text{čiže} \ \ \ \ \frac{v_1}{v_2}=\frac{1}{3}\cdot \frac{|AB|}{|CD|}=\frac{1}{3}\cdot \frac{3}{2}=\frac{1}{2}.\] Z vyznačených dvojíc podobných pravouhlých trojuholníkov vyplýva, že v práve určenom pomere \(2 : 1\) výšok \(v_2\) a \(v_1\) delí aj bod \(M\) rameno \(AD\) a bod \(N\) rameno \(BC\) (v prípade pravého uhla pri jednom z vrcholov \(A\) či \(B\) je to zrejmé rovno). Tým je konštrukcia bodov \(M\) a \(N\), a teda aj úsečky \(MN\) určená. Teraz zistíme, v akom pomere ju delí uvažovaný bod \(P\).
Keďže obsahy trojuholníkov \(BCP\) a \(DAP\) sú v pomere \(3 : 1\), platí \[\bigg(\frac{|NP|v_1}{2}+\frac{|NP|v_2}{2}\bigg): \bigg(\frac{|MP|v_1}{2}+\frac{|MP|v_2}{2}\bigg)= 3 : 1,\] \[\frac{|NP|(v_1 + v_2 )}{2}: \frac{|MP|(v_1 + v_2 )}{2}= 3 : 1, \ \ \ \ |NP| : |MP| = 3 : 1.\] Tým je konštrukcia (jediného) vyhovujúceho bodu \(P\) úplne opísaná.
b) Doplňme trojuholník \(DAC\) na rovnobežník \(DAXC\). Jeho strana \(CX\) delí priečku \(MN\) na dve časti, a keďže \(v_1 =\frac{1}{3}v\), môžeme dĺžku priečky \(MN\) vyjadriť ako \(|MN| = |MY | + |Y N| = |AX| +\frac{1}{3} |XB| = |CD| +\frac{1}{3} (|AB| - |CD|) = \frac{1}{3}|AB| +\frac{2}{3}|CD| = \frac{7}{6}|CD|\), lebo podľa zadania platí \(|AB| =\frac{3}{2}|CD|\). Preto \[|MP| =\frac{1}{4}|MN| =\frac{1}{4} \cdot \frac{7}{6}|CD| = \frac{7}{24}|CD|,\] takže pre pomer obsahov trojuholníkov \(CDP\) a \(DAP\) platí \[\frac{|CD|v_1}{2}:\frac{|MP|(v_1 + v_2 )}{2}= (|CD|v_1 ) : \bigg( \frac{7}{24}\cdot |CD| \cdot 3v_1\bigg)= 1 :\frac{7}{8} = 8 : 7.\] Pomer obsahov trojuholníkov \(BCP\) a \(CDP\) je teda \(21 : 8\) a pomer obsahov trojuholníkov \(ABP\) a \(BCP\) je tak \(24 : 21\). Postupný pomer obsahov trojuholníkov \(ABP\), \(BCP\), \(CDP\) a \(DAP\) je preto \(24 : 21 : 8 : 7\).
Komentár
Táto komplexná úloha je vrcholom tohto seminárneho stretnutia. Vyžaduje umnú prácu s pomermi obsahov, podobnými trojuholníkmi aj netriviálny nápad doplnenia trojuholníka \(DAC\) na rovnobežník. Je tak vhodné skôr než samostatne úlohu riešiť spoločne na tabuľu. Študentom tiež pripomenieme, že podobne ako v úvodnej úlohe, aj tu našlo vhodné rozdelenie zadaného útvaru svoje opodstatnenie a prispelo k úspešnému rozklúsknutiu problému.Úloha 66-I-5-D2
Riešenie*
Úloha 57-II-3
Riešenie*
Ak \(n = 5\), existuje medzi zostávajúcimi osobami aspoň päť ďalších dvojíc známych. Ktorákoľvek z týchto dvojíc potom tvorí s osobou A trojicu známych.
Ak \(n = 4\), existuje osoba \(B\), ktorá sa s \(A\) nepozná, a tá má tiež najviac štyroch známych. Preto sa medzi známymi osoby \(A\) vyskytujú aspoň dve dvojice známych. Osoba \(A\) s jednou z týchto dvojíc tvorí opäť trojicu známych.
Situácia \(n\leq 3\) nemôže nastať, pretože celkový počet dvojíc známych v Skupine by vtedy bol nanajvýš \(\frac{1}{2}\cdot 6n \leq 9\).
Príklad skupiny šiestich osôb s deviatimi dvojicami, ale s žiadnou trojicou známych, je znázornený grafom na . V ňom body \(A\), \(B\), \(C\), \(D\), \(E\) a \(F\) predstavujú jednotlivé osoby a dvojice známych sú vyznačené úsečkami. Pritom žiadne tri z úsečiek netvoria trojuholník. Pokiaľ je v Skupine menej ako deväť dvojíc známych, zostrojíme vhodný príklad odstránením príslušného počtu úsečiek z (pritom určite žiadny trojuholník nevznikne).
Iné riešenie*. Ak je v šestici osôb aspoň 10 dvojíc známych, je v nej najviac 5 dvojíc neznámych, lebo všetkých dvojíc je práve 15. Budeme preto naopak predpokladať, že v každej trojici sa nájde dvojica neznámych, a dokážeme, že v celej šestici je takých dvojíc aspoň 6. Pri uvedenom predpoklade môžeme označenie osôb zvoliť tak, aby v trojiciach \(ABC\) a \(DEF\) boli dvojice neznámych \(AB\) a \(DE\). Potom ďalšie štyri rôzne dvojice neznámych nájdeme (po jednej) v trojiciach \(ACD\), \(AEF\), \(BCE\), \(BDF\) (presvedčte sa, že každá dvojice sa vyskytuje najviac v jednej z uvedených štyroch trojíc a žiadna z týchto trojíc neobsahuje ani dvojicu \(AB\), ani dvojicu \(DE\)). Príklad pre menší počet dvojíc známych zostrojíme rovnako ako v predchádzajúcom riešení.
Úloha 59-S-3
Riešenie*
\(b - a = 1\) a \(a + b - 1 = 2\), potom \(a = 1\) a \(b = 2.\)
\(b - a = 2\) a \(a + b - 1 = 1\), potom \(a = 0\) a \(b = 2\).
\(b - a = -1\) a \(a + b - 1 = -2\). Druhú rovnicu možno prepísať na tvar \(a + b = -1\), z ktorého vidíme, že rovnosť nenastane pre žiadnu dvojicu nezáporných celých čísel.
\(b - a = -2\) a \(a + b - 1 = -1\). Druhú rovnicu možno prepísať na tvar \(a + b = 0\), z ktorého vidíme, že vyhovuje jediná dvojica nezáporných celých čísel \(a = b = 0\), ktorá však nevyhovuje prvej rovnici.
Záver. Úloha má dve riešenia: Buď \(a = 1\) a \(b = 2\), alebo \(a = 0\) a \(b = 2\).
Poznámka. Namiesto rozboru štyroch možností môžeme začať úvahou, že nulové čísla \(a, b\) nie sú riešením úlohy, takže \(a + b - 1 = 0\), a teda aj \(b - a = 0\). Stačí teda uvažovať iba možnosti a) a b).
Iné riešenie*. Rovnicu upravíme na tvar \(2 = (b^2 - b) - (a^2 - a)\), resp. na tvar \(2 = b(b - 1)-a(a-1)\). Z nasledujúcej tabuľky a tvaru čísel \(x^2 -x = x(x-1)\) je zrejmé, že rozdiely medzi susednými hodnotami výrazov \(x(x - 1)\) rastú s rastúcim \(x\) (ľahko sa o tom presvedčíme výpočtom: \((x + 1)x - x(x - 1) = 2x\)).
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | … |
|---|---|---|---|---|---|---|---|
| \(x(x-1)\) | 0 | 0 | 2 | 6 | 12 | 20 | … |
Môže teda platiť iba \(b^2 - b = 2\) a \(a^2 - a = 0\). Odtiaľ \(a \in \{0, 1\}\) a \(b = 2\). Riešením úlohy sú teda dve dvojice nezáporných celých čísel: \(a = 0, b = 2\) a \(a = 1, b = 2\).
Komentár
Úloha je (okrem iného) zaujímavá tým, že poskytuje priestor na rôznorodé prístupy k riešeniu a môže byť dobrým podnetom na vzájomné vysvetľovanie riešení medzi študentmi. Kľúčovým prvkom riešenia je úprava rovnice na vhodný tvar – na tomto mieste je študentom vhodné pripomenúť, že zručnosť a dôvtip pri manipulácii s algebraickými výrazmi nájdu uplatenie v širokom spektre problémov, nielen na prvom seminárnom stretnutí, ktoré na túto problematiku bolo zamerané.Úloha 65-S-1
Riešenie*
Odpoveď. Vyhovujú tri čísla 1 264, 1 580 a 1 896.
Poznámka. Namiesto štyroch neznámych cifier \(a\), \(b\), \(c\), \(d\) možno na zápis rovnice zo zadania využiť zrejme priamo obe dvojciferné čísla \(x = ab\) a \(y = cd\). Rovnica potom bude mať tvar \(100x+y = 20x+16y\), ktorý podobne ako v pôvodnom postupe upravíme na \(80x = 15y\), čiže \(16x = 3y\). Teraz namiesto vzťahu \(16 \mid y\) môžeme využiť druhý podobný dôsledok \(3 \mid x\) a uvedomiť si, že z odhadu \(y \leq 99\) vyplýva \(16x \leq 3 \cdot 99 = 297\), odkiaľ \(x \leq 18\), čo spolu s odhadom \(x \geq 10\) vedie k možným hodnotám \(x \in\) {12, 15, 18}. Z rovnice \(16x = 3y\) potom už dopočítame \(y = 64\) pre \(x = 12\), \(y = 80\) pre \(x = 15\) a \(y = 96\) pre \(x = 18\).
Úloha 62-I-1
Riešenie*
V prvom prípade bude päť zo šiestich 3-skokov doprava (a všetky 2-skoky nadol), takže cesta bude určená len poradovým číslom toho (jediného) 3-skoku, ktorý bude smerovať nadol. Preto je ciest tohto typu práve 6.
V druhom prípade bude cesta určená poradovými číslami troch 3-skokov doprava a poradovými číslami troch 2-skokov doprava. Výbery oboch trojíc sú nezávislé ( t. j. možno ich spolu ľubovoľne kombinovať) a pri každom z nich vyberáme tri prvky zo šiestich, čo možno urobiť 20 spôsobmi.1 Preto je ciest tohto typu \(20 \cdot 20 = 400\).
V treťom prípade je kobylkina cesta určená len poradovým číslom toho jediného 3-skoku, ktorý bude smerovať doprava, takže ciest tohto typu je (rovnako ako v prvom prípade) opäť 6.
Záver. Hľadaný celkový počet kobylkiných ciest je 6 + 400 + 6 = 412.
Iné riešenie*. Zadanú úlohu ”pre pravé dolné políčko“ vyriešime tak, že budeme postupne určovať počty kobylkiných ciest, ktoré vedú do jednotlivých políčok tabuľky (políčka budeme postupne voliť od ľavého horného políčka po jednotlivých vedľajších diagonálach2, lebo ako ľahko zistíme, po určitom počte skokov skončí kobylka na tej istej vedľajšej diagonále; tak sa nakoniec dostaneme k tomu najvzdialenejšiemu, teda pravému dolnému políčku). Pre zjednodušenie ďalšieho výkladu označme \((i, j)\) políčko v \(i\)-tom riadku a \(j\)-tom stĺpci.
Je zrejmé, že povoleným spôsobom skákania sa kobylka vie dostať len na niektoré políčka celej tabuľky. Po prvom skoku (ktorý musí byť 2-skok z políčka (1, 1)) sa kobylka dostane len na políčko (1, 3) alebo (3, 1), po druhom skoku (teda 3-skoku) to bude niektoré z políčok \[(1, 6), (3, 4), (4, 3), (6, 1).\] Vo všetkých doteraz uvedených políčkach je v tabuľke vpísané číslo 1, lebo na každé z nich vedie jediná kobylkina cesta. Situácia sa zmení po treťom skoku (2-skoku) kobylky, lebo na políčka (3, 6) a (6, 3) vedú vždy dve rôzne cesty, a to z políčok (1, 6) a (3, 4), resp. z políčok (6, 1) a (4, 3). Takto v ďalšom kroku našej úvahy určíme všetky políčka, na ktoré sa kobylka môže dostať po štyroch skokoch, aj počty ciest, ktoré v týchto políčkach končia. V zapĺňaní tabuľky týmito číslami (postupom podľa počtu skokov kobylky) pokračujeme, až sa dostaneme do políčka (16, 16). Pritom neustále využívame to, že posledný skok kobylky na dané políčko má danú dĺžku a jeden či oba možné smery. V prvom prípade číslo z predposledného políčka na ceste na posledné políčko opíšeme, v druhom prípade tam napíšeme súčet čísel z oboch možných predposledných políčok.
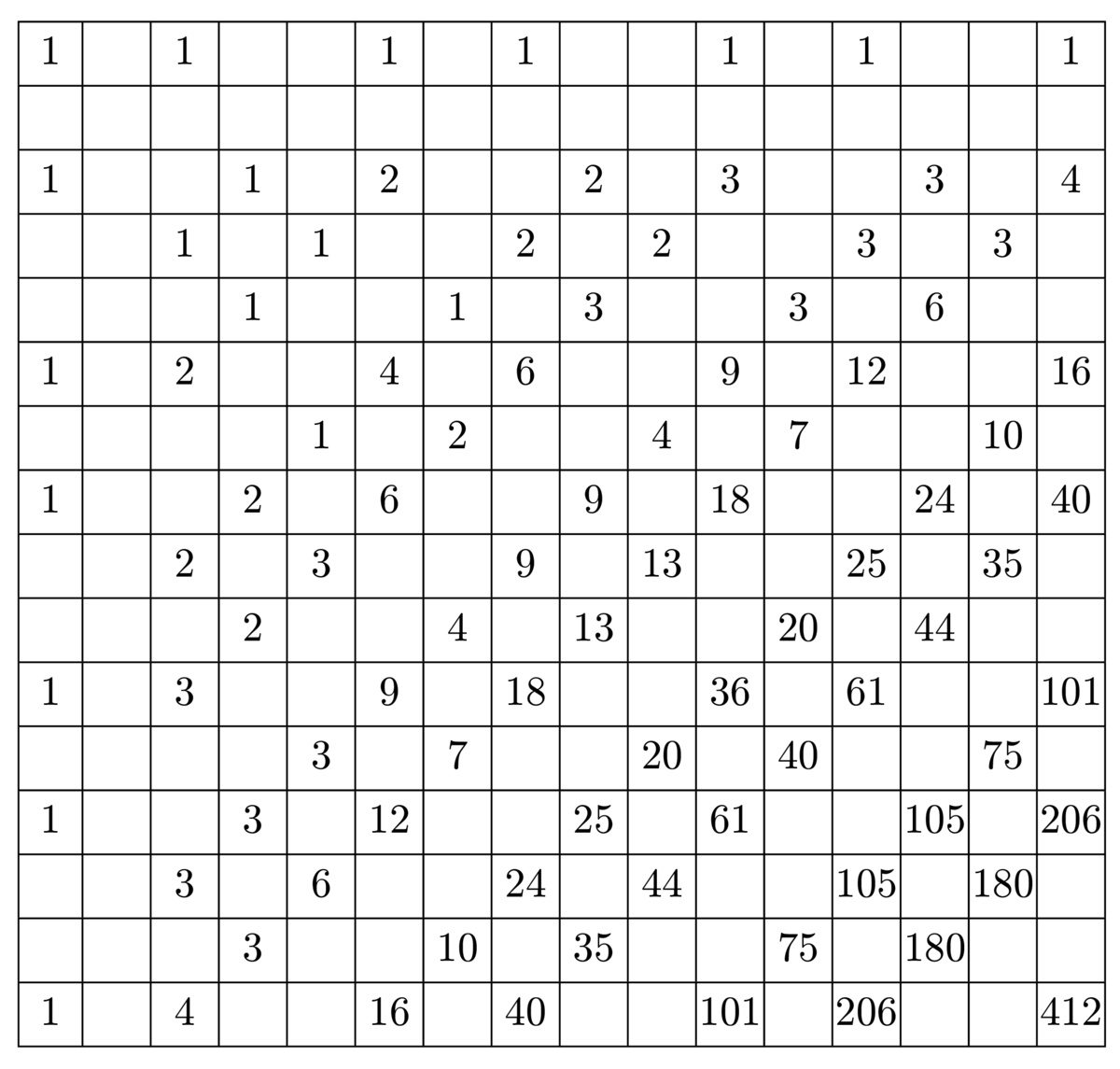
Rovnako ako v prvom riešení prichádzame k výsledku 412.
Väčšina riešiteľov kategórie C ešte zrejme nepozná kombinačné čísla, hodnotu \(\binom{6}{3}=20\) však možno vypočítať aj vypísaním jednotlivých možností.↩︎
V tomto prípade pod vedľajšou diagonálou chápeme skupinu políčok, ktorých stredy ležia na priamke kolmej na spojnicu stredu začiatočného políčka so stredom koncového políčka.↩︎
Úloha 66-II-4
Riešenie*
Iné riešenie*. Dokazovanú nerovnosť postupne upravíme, pričom využijeme známu nerovnosť \(b/c + c/b \geq 2\), ktorá je pre kladné čísla \(b, c\) ekvivalentná s nerovnosťou \((b - c)^2\geq 0\): \[(-a + b + c)\bigg( \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\bigg) = 1+\bigg(\frac{b}{a}-\frac{a}{b}\bigg)+\bigg(\frac{c}{a}-\frac{a}{c}\bigg)+\bigg(\frac{b}{c}+\frac{c}{b}\bigg)\geq\] \[\geq 1+\frac{b^2-a^2}{ab}+\frac{c^2-a^2}{ac}+2\geq 3,\] pretože zrejme platí aj \(a^2\leq b^2\leq c^2\).
Iné riešenie*. Podľa predpokladov úlohy platia nerovnosti \(-a + b + c \geq c\) a \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \frac{2}{b}+\frac{1}{c}\). Obe nerovnosti (s kladnými stranami) medzi sebou vynásobíme a získame tak \[(-a + b + c)\bigg(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\bigg) \geq c \bigg( \frac{2}{b}+\frac{1}{c}\bigg)=1 +\frac{2c}{b}\geq 3\] pretože \(c/b \geq 1\) podľa zadania.
Komentár
Ďalšia úloha, ktorú je možné rozlúsknuť spektrom rozličných prístupov. Ak študenti zvolia len cestu ekvivalentných úprav, ukážeme im aj riešenie, ktoré využíva nerovnosť \(b/c+c/b \geq 2\) z predchádzajúceho seminára o nerovnostiach, rovnako ako riešenie pomocou vynásobenia nerovností medzi sebou. Takto dáme študentom príležitosť poznať aj iné prístupy, ktoré môžu byť užitočné pri ďalšom riešení úloh.Úloha 62-I-4-N7
Riešenie*
Úloha 60-S-1
Riešenie*
Poznámka. Úlohu možno riešiť aj úvahou: za 40 minút ubehnú atléti spolu 4 okruhy (to vyplýva z prvej podmienky), pritom rýchlejší o 1 okruh viac ako pomalší (to vyplýva z druhej podmienky). To teda znamená, že prvý za uvedenú dobu ubehne 2,5 okruhu a druhý 1,5 okruhu, takže rýchlejší ubehne jeden okruh za 40/2,5 = 16 minút.
Komentár
V tomto prípade vyžaduje netriviálne úsilie správne zostavenie sústavy rovníc tak, aby skutočne zodpovedala zadaniu. Jej vyriešenie potom už zložité nie je. Za zmienku stojí, že úloha je vhodným príkladom situácie, v ktorej si zmysluplnosť výsledku môžeme aspoň približne overiť (záporné rýchlosti, rýchlosti väčšie ako rýchlosť svetla).Úloha 66-I-2-N2
Riešenie*
Komentár
Úloha stavia na myšlienke deliteľnosti rozdielu \(U(n)\) a \(V(n)\) hľadaným \(d\), čo je ďalší užitočný nástroj: namiesto upravovania výrazov \(U(n)\) a \(V(n)\) ich odčítať. Taktiež je vhodné upozorniť študentov, že druhá časť riešenia – dokázanie, že nájdené riešenie je jediné – je taktiež podstatnou súčasťou riešenia (nielen) tejto úlohy.Úloha B-65-I-5
Riešenie*

\(AB\) a \(CD\) pri vrcholoch \(E\) a \(F\) dostávame \[|\measuredangle GEH| = |\measuredangle AEB| = |\measuredangle CFD| = |\measuredangle GFH|,\] čo znamená, že body \(E\), \(F\), \(G\) a \(H\) ležia na jednej kružnici, pretože vrcholy zhodných uhlov \(GEH\) a \(GFH\) ležia v rovnakej polrovine s hraničnou priamkou \(GH\). Z toho vyplýva, že uhly \(EFH\) a \(EGH\) nad jej tetivou \(EH\) sú zhodné. To spolu so zhodnosťou uhlov \(EFD\) a \(EAD\) nad tetivou \(ED\) pôvodnej kružnice (obr. 1) vedie na zhodnosť súhlasných uhlov \(EGH\) a \(EAD\) priečky \(AE\) priamok \(GH\) a \(AD\), ktoré sú teda naozaj rovnobežné. Tým je tvrdenie úlohy dokázané.
Komentár
Umiestnenie vrcholov šesťuholníka na kružnici priam nabáda, aby študenti hľadali dvojice rovnakých uhlov, ktoré im potom pomôžu vyvodiť závery o (ne)rovnobežnosti skúmaných úsečiek. Zároveň úloha obsahuje zaujímavú druhú časť, kedy objavíme, že body \(E, F, G, H\) ležia na jednej kružnici.Úloha 58-I-2-D3
Riešenie*
Úloha 60-I-5-D3
Riešenie*
Komentár
Úloha je zaujímavá tým, že prácu s najväčším spoločným deliteľom obsahuje nepriamo a využíva tiež poznatky o deliteľnosti z minulého seminára.Úloha B-59-I-6
Dokážte nerovnosť \(b > 3\).
Pomocou \(b\) vyjadrite korene oboch rovníc.
Riešenie*
Keďže \(x_2 - x_1 > 0\) a \(b + 1 > 0\), musí byť aj \(x_1 > 0\); z [eq:B59I6_1] máme \(x_1 =\sqrt{(b - 3)/2}\) a ďalej \[x_2 =\frac{b-1}{x_1}=\frac{(b - 1)\sqrt{2}}{\sqrt{b-3}}.\] Korene druhej rovnice sú potom \[x_2 - x_1 = \frac{b+1}{} \ \ \ \ \text{a} \ \ \ \ 2x_1=\sqrt{2(b - 3)}.\]
Iné riešenie*. Korene prvej rovnice sú \[x_1 = \frac{a -\sqrt{a^2 - 4b + 4}}{2}, \ \ \ \ x_2 =\frac{a +\sqrt{a^2 - 4b + 4}}{2},\] pričom pre diskriminant máme \[\label{eq:B59I6_2}
D = a^2 - 4(b - 1) > 0.\] Rozdiel koreňov \(x_2 - x_1 =\sqrt{a^2 - 4b + 4}\) je koreňom druhej rovnice, a preto \[\label{eq:B59I6_3}
\begin{aligned}
a^2 - 4b + 4 - a \sqrt{a^2 - 4b + 4} + b + 1 &= 0,\\
a^2 - 3b + 5 &= a\sqrt{a 2 - 4b + 4},\\
a^4 + 2a^2 (5 - 3b) + (3b - 5)^2 &= a^4 - 4a^2 b + 4a^2,\\
(3b - 5)^2 &= a^2 (2b - 6).
\end{aligned}\] Rovnosť \(a = 0\) nastáva práve vtedy, keď \(3b - 5 = 0\); potom by ale neplatilo [eq:B59I6_2]. Preto \(a^2 > 0\), \((3b - 5)^2 > 0\), a teda aj \(2b - 6 > 0\), čiže \(b > 3\). Z [eq:B59I6_2] a [eq:B59I6_3] potom vyplýva \(a > 0\), a teda \(a = (3b - 5)/\sqrt{2(b - 3)}\); ďalej potom \[\begin{aligned}
x_1 &=\frac{1}{2}\bigg( \frac{3a-5}{\sqrt{2(b-3)}}-\sqrt{\frac{(3b-5)^2}{2(b-3)}}-4b+4\bigg)=\sqrt{\frac{b-3}{2}},\\
x_2 &=\frac{1}{2} \bigg( \frac{3a-5}{\sqrt{2(b-3)}}+\sqrt{\frac{(3b-5)^2}{2(b-3)}}-4b+4\bigg)=\frac{(b-1)\sqrt{2}}{\sqrt{b-3}}.\end{aligned}\] Druhá rovnica má korene \[\begin{aligned}
x_3 &=\frac{a-\sqrt{a^2-4b-4}}{2}=\frac{b+1}{\sqrt{2(b-3)}}=x_2-x_1\\
x_4 &=\frac{a+\sqrt{a^2-4b-4}}{2}=\sqrt{2(b-3)}.\end{aligned}\]
Komentár
Úloha sa dá vyriešiť relatívne vyjadrením koreňov prvej rovnice, dosadením ich rozdielu do druhej rovnice a odpovedajúcou diskusiou. Takýto prístup je síce zrozumiteľný, avšak dosť pracný. Ak študenti neprídu na prvý spôsob riešenia, považujeme za vhodné im ho ukázať ako dobrý príklad toho, ako nám použitie Viètovych vzorcov môže výraznej zjednodušiť výpočet.Úloha 62-I-4-N6
Riešenie*
Úloha 61-I-5-N3
Riešenie*
Úloha 66-I-3-D1
Riešenie*
Úloha B-59-I-3
Riešenie*
Úsečka \(KL\) je strednou priečkou rovnobežníka \(ABCD\), preto \(KL \parallel MD\); \(KLDM\) je teda lichobežník, a pretože sa mu dá opísať kružnica, je rovnoramenný; odtiaľ \(|KM|= |DL| = \frac{1}{2}a\). Keďže \(KM\) je stredná priečka trojuholníka \(BDA\), má strana \(BD\) dĺžku \(2 \cdot |KM| = a\). Bod \(D\) teda leží na kružnici so stredom \(B\) a polomerom \(a\).
Konštrukcia. Zostrojíme stred \(K\) úsečky \(AB\), os \(o\) úsečky \(AK\) a kružnicu \(k\) so stredom \(B\) a polomerom \(|AB|\). Priesečník tejto kružnice s osou úsečky \(AK\) je bod \(D\). Bod \(C\) je potom priesečník priamok vedených bodmi \(D\) a \(B\) rovnobežne s priamkami \(AB\) a \(AD\).
Dôkaz správnosti konštrukcie. Štvoruholník \(ABCD\) má protiľahlé strany rovnobežné, je to teda rovnobežník. Označíme \(L\) a \(M\) stredy úsečiek \(CD\) a \(AD\). Z toho, že bod \(D\) leží na osi úsečky \(AK\), vyplýva \(|KD| = |AD|\). Keďže \(KBLD\) je rovnobežník, platí \(|BL| = |KD| = |AD|\). Lichobežník \(ABDL\) je teda rovnoramenný, a preto body \(A\), \(B\), \(L\), \(D\) ležia na jednej kružnici. Úsečka \(KM\) je stredná priečka trojuholníka \(BDA\), preto \(|KM| = \frac{1}{2}|BD|= \frac{1}{2}|AB| = |DL|\); \(KLDM\) je teda rovnoramenný lichobežník, a preto jeho vrcholy ležia na jednej kružnici.
Diskusia. Priamka \(o\) má od bodu \(B\) menšiu vzdialenosť ako bod \(A\), takže pretína kružnicu \(k\) v dvoch bodoch. Úloha má teda v každej polrovine s hraničnou priamkou \(AB\) jedno riešenie.
Iné riešenie*. Tak ako v prvom riešení dokážeme, že \(|KD| = |AD|\) a \(|DB| = |AB|\). Trojuholníky \(AKD\) a \(DAB\) sú teda rovnoramenné, a keďže sa zhodujú v uhle pri vrchole \(A\), sú podobné. Preto \(|AK|/|AD| = |DA|/|AB|\), čiže \(\frac{1}{2}a/b = b/a\) a odtiaľ \(b = \frac{1}{2}a\sqrt{2}\). Bod \(D\) je teda priesečníkom kružníc so stredmi \(A\) a \(K\) a polomerom \(\frac{1}{2}a\sqrt{2}\).
Úloha 60-I-2-N2
Riešenie*
Úloha 58-I-1-D1
Riešenie*
Úloha 65-I-4-D1
Riešenie*
Úloha 63-II-4
Riešenie*
a \(EDC\) majú spoločnú stranu \(ED\), pomer ich obsahov je teda rovný pomeru prislúchajúcich výšok. Ak navyše postupne označíme \(P, Q\) a \(R\) kolmé priemety vrcholov \(A, B\) a \(C\) na priamku \(DE\) a označíme \(v = |AP|\), \(w = |BQ| = |CR|\), dostaneme z podobných pravouhlých trojuholníkov \(AEP\) a \(BEQ\) úmeru \[\frac{18}{S}=\frac{v}{w}=\frac{|AE|}{|EB|}.\] Analogicky pre trojuholníky \(ECD\) a \(ECB\) zistíme, že \[\frac{8}{S}=\frac{|EB|}{|AE|}.\] (V obr. 1 sú prislúchajúce priemety iba naznačené, ale jedná sa o ten istý výpočet ako v predošlom odseku, len v ňom zameníme zodpovedajúce body \(A\leftrightarrow B, C \leftrightarrow D\) a prislúchajúce obsahy trojuholníkov \(AED\) a \(BEC\).) Dokopy teda je \(S : 8 = 18 : S\) čiže \(S^2 = 144\), takže trojuholník \(ECD\) má obsah \(S = 12\) cm\(^2\) .
Úloha 62-I-1-D1
Riešenie*
Úloha 66-I-2-D2
Riešenie*
Úloha 64-I-2-N2
Riešenie*
Úloha 61-I-4
Dokážte, že medzi číslami \(a, b, c, d\) sa nájdu dve so súčtom najviac 4.
Akú najmenšiu hodnotu môže mať súčet \(a^2 + b^2 + c^2 + d^2\)?
Riešenie*
Komentár
Ďalšia úloha, ktorá nepracuje s priamym dokazovaním nerovností, avšak využíva fakt, ktorý sme si osvojili už pri prvom nerovnostnom seminári, a to že druhá mocnina ľubovoľného reálneho čísla je vždy nezáporná. To nám potom pomohlo uskutočniť odhad hodnoty súčtu zo zadania úlohy. Na tomto mieste považujeme sa vhodné študentom zmieniť, že odhadovanie hodnôt je ďalším miestom, kde sa znalosti o nerovnostiach výborne uplatnia, ako ukáže aj nasledujúca úloha.Úloha 61-I-6
Riešenie*
Ak je celkový počet políčok hracej plochy nepárny (v zadaní pre \(n = 5\)), môže v poradí prvá hráčka pomýšľať na túto víťaznú stratégiu: spárovať všetky políčka hracej dosky okrem jedného do dvojíc tak, aby v každom páre boli políčka navzájom dosiahnuteľné jedným skokom. Pokiaľ také spárovanie prvá hráčka nájde, má víťaznú stratégiu: v prvom ťahu položí figúrku na (jediné) nespárované políčko a v každom ďalšom ťahu urobí skok na druhé políčko toho páru, na ktorého prvom políčku figúrka práve leží.
Nájsť požadované spárovania políčok je pre zadané príklady ľahké a je to možné urobiť viacerými spôsobmi. Ukážme tie z nich, ktoré majú určité črty pravidelnosti. Na obr. 1 zľava je vidno, ako je možné spárovať políčka časti hracej plochy o rozmeroch \(4\times 2\); celú hraciu plochu \(4 \times 4\) rozdelíme na dva také bloky a urobíme spárovanie v každom z nich. I na spárovanie políčok hracej plochy \(6\times 6\) môžeme využiť spárovanie v dvoch blokoch \(4 \times 2\); na obr. 1 uprostred je znázornené možné stredovo súmerné spárovanie všetkých políčok. Nakoniec na obr. 1 vpravo je príklad spárovania políčok hracej plochy \(5 \times 5\) s nespárovaným políčkom v ľavom hornom rohu (nespárované políčko nemusí byť nutne rohové); opäť je pritom využitý jeden blok \(4 \times 2\).

Úloha 63-I-1-N5
Riešenie*
Úloha B-58-I-5-D2
Riešenie*
Úloha 63-I-6-N2
a) Aký najväčší a aký najmenší počet bodov mohol mať? b) Koľko partií mohlo skončiť remízou, ak na konci turnaja mali všetci účastníci rôzne počty bodov?
Riešenie*
Úloha 57-II-2
Riešenie
Záver. Klárka násobila čísla 57 a 75.
Úloha 61-I-6-N3
Riešenie*
Komentár
Úloha je zaujímavým príkladom, kde zohráva špeciálnu úlohu jeden konkrétny bod hracej plochy. Nájdenie víťaznej stratégie je po uvedomení si tejto vlastnosti už úlohou jednoduchou. Na príklade tejto hry môžeme študentov upozorniť na ďalší všeobecný princíp, ktorý pri riešení matematických problémov môže prísť vhod – hľadanie symetrií, príp. špeciálnych bodov týchto symetrií a skúmanie ich vlastností, pričom symetrie nemusíme chápať nutne iba v geometrickom kontexte.Úloha B-65-I-5-N2
Riešenie*
Úloha (Holton 2010), úloha 38, str. 115
Riešenie*
Komentár
Úloha nie je náročná a je zaradená ako zahrievacie cvičenie a ukážka práce s deliteľnosťou zloženým číslom.Holton, Derek Allan. 2010. A First Step to Mathematical Olympiad Problems. 1st edition. Danvers, USA: World Scientific.
Úloha B-64-II-4
Riešenie*
Ukážeme, že vyhrávajúcu stratégiu má Marek. Najskôr do menovateľa zlomku pre koeficient \(b\) napíše \(1\).
Ak Tomáš obsadí vo svojom prvom ťahu iné miesto ako v čitateli \(b\), napíše do neho Marek v nasledujúcom ťahu najväčšie zostávajúce číslo zo zoznamu (teda 5 alebo 6). Hodnota \(b^2\) potom bude aspoň 25 a zo zvyšných čísel možno zostaviť výraz \(4ac\) s hodnotou nanajvýš \(4\cdot \frac{6\cdot 4}{3\cdot 2}= 16\). Diskriminant vzniknutej kvadratickej rovnice tak bude určite kladný.
Predpokladajme, že Tomáš vo svojom ťahu doplní čitateľa \(b\). Marek potom v druhom ťahu napíše najmenšie zostávajúce číslo zo zoznamu (2 alebo 3) do čitateľa \(a\) (alebo \(c\)).
V prípade, že Tomáš v prvom ťahu napísal do čitateľa \(b\) číslo 2, je hodnota \(b^2\) rovná 4 a najväčšia možná hodnota \(4ac\) (s prihliadnutím na druhý Marekov ťah) je \(4 \cdot \frac{3\cdot 6}{4\cdot 5}=\frac{18}{5}\leq 4\), teda diskriminant vzniknutej kvadratickej rovnice bude opäť kladný.
V prípade, že Tomáš v prvom ťahu napísal do čitateľa \(b\) iné číslo ako 2, je hodnota \(b^2\) aspoň 9 a hodnota \(4ac\) je nanajvýš \(4 \cdot \frac{2\cdot 6}{3\cdot 4} = 4\), takže diskriminant vzniknutej kvadratickej rovnice bude aj v tomto prípade kladný.
Záver. V danej hre môže vyhrať Marek nezávisle na ťahoch Tomáša. Jeho víťazná stratégia je opísaná vyššie.
Komentár
Posledná úloha je zaujímavým spojením hľadania víťaznej stratégie a analýzy vlastností diskriminantu kvadratickej rovnice. Študentov necháme riešenie úlohy hľadať samostatne a potom ich vyzveme, aby stratégiu, ktorú našli, použili pri hre so spolužiakmi. Bude zaujímavé pozorovať, či nastane situácia, v ktorej aj neoptimálna stratégia zvíťazí.Úloha 63-S-1
Riešenie*
Záver. Za daných podmienok nadobúda výraz \(V\) iba hodnotu 0.
Iné riešenie*. Podmienky úlohy si predstavíme ako sústavu rovníc s neznámymi \(a, b\) a parametrami \(c, d\). Vyriešením tejto sústavy (sčítacou alebo dosadzovacou metódou) vyjadríme \(a = 2 - c, b = -d \ (c, d \in \RR )\) a po dosadení do výrazu \(V\) dostávame \[V = (2 - c)(-d) - dc + cd + d(2 - c) = 0.\]
Komentár
Zadanie úlohy opäť obsahuje sústavu dvoch rovníc. Jej riešenie sa však po substitúcii zredukuje na veľmi jednoduchú sústavu, s ktorou sa študenti stretli už na základnej škole, takže by nemala spôsobiť výrazné problémy.Úloha 65-II-3
Riešenie*
Z predpokladu \(S_{APCD} =\frac{1}{2}S_{ABCD}\) vyplýva pre druhú polovicu obsahu \(ABCD\) vyjadrenie \(\frac{1}{2}S_{ABCD} = S_{PBC}\), takže \(S_{APCD} = S_{PBC}\) čiže \(cv =\frac{1}{2}|PB|v\), odkiaľ vzhľadom na to, že \(v \neq 0\), vychádza \(|PB| = 2c\), v dôsledku čoho \(|AB| = 3c\).
Trojuholníky \(CDK\) a \(PBK\) majú pravé uhly pri vrcholoch \(C\), \(P\) a zhodné (vrcholové) uhly pri spoločnom vrchole \(K\), takže sú podľa vety \(uu\) podobné, a to s koeficientom \(|PB| : |CD| = 2c : c = 2\). Preto tiež platí \(|PK| : |CK| = 2 : 1\), odkiaľ \(|KP| =\frac{2}{3}v\) a \(|CK| =\frac{1}{3}v\).
Posudzované obsahy trojuholníkov \(ABC\) a \(BCK\) tak majú vyjadrenie \[S_{ABC} = \frac{|AB| \cdot |CP|}{2}=\frac{3cv}{2} \ \ \ \ \text{a} \ \ \ \ S_{BCK} =\frac{|CK|\cdot |BP|}{2}=\frac{\frac{1}{3}v\cdot 2c}{2}=\frac{cv}{3},\] preto ich pomer má hodnotu \[\frac{S_{BCK}}{S_{ABC}}=\frac{\frac{1}{3}cv}{\frac{3}{2}cv}=\frac{2}{9}.\] Záver. Trojuholník \(BCK\) zaberá \(2/9\) obsahu trojuholníka \(ABC\).
Komentár
Najkomplexnejšia úloha tohto seminára precvičí študentov v používaní vlastností podobných trojuholníkov a taktiež vo vyjadrovaní obsahov trojuholníkov pomocou určiteľných hodnôt. Tvorí tak dôstojnú bodku za týmto seminárom.Keďže podľa zadania uhlopriečka \(BD\) pretína výšku \(CP\), musí jej päta \(P\) ležať medzi bodmi \(A\) a \(B\), takže ide o lichobežník \(ABCD\) s dlhšou základňou \(AB\) a kratšou základňou \(CD\).↩︎
Úloha 60-I-3-D3
Riešenie*
Úloha 60-I-5-N4
Riešenie*
Úloha 65-I-6
Riešenie*
Hľadaný obsah trojuholníka \(KLM\) vyjadríme nie pomocou dĺžok jeho odvesien \(KL\) a \(LM\), ale pomocou dĺžok jeho prepony \(KM\) a k nej prislúchajúcej výšky \(LD\) (, teda použitím vzorca1
\[S_{KLM} = \frac{|KM| \cdot |LD|}{2}.\]
Na určenie vzdialeností bodu \(D\) od bodov \(B\) a \(L\) uvažujme ešte stred S úsečky \(BL\) (). Trojuholníky \(ASB\) a \(LDB\) sú oba pravouhlé so spoločným ostrým uhlom pri vrchole \(B\). Sú preto podľa vety \(uu\) podobné, takže pre pomer ich strán platí (počítame s dĺžkami bez jednotiek, takže podľa zadania je \(|AB| = 4\), \(|BL| = 2\), a preto \(|BS| = |BL|/2 = 1\))
\[\frac{|BD|}{|BS|}=\frac{|BL|}{|BA|}=\frac{2}{4}, \ \ \ \text{odkiaľ} \ \ \ |BD| =\frac{1}{2}|BS| =\frac{1}{2}.\] Z Pytagorovej vety pre trojuholník \(LDB\) tak vyplýva2
\[|LD| =\sqrt{|BL|^2-|BD|^2}=\sqrt{4-\frac{1}{4}}=\frac{\sqrt{15}}{2}.\]
Z rovnosti \(|BD| = 1/2\) už odvodíme aj dĺžku úseku \(KD\) prepony \(KM\) pravouhlého trojuholníka \(KLM\): \(|KD| = |AB| - |AK| - |BD| = 4 - 1 - 1/2 = 5/2\). Dĺžku druhého úseku \(DM\) teraz určíme z Euklidovej vety o výške, podľa ktorej \(|LD|^2 = |KD| \cdot |DM|\). Dostaneme teda \(|DM| = |LD|^2 /|KD| = (15/4)/(5/2) = 3/2\), čiže celá prepona \(KM\) má dĺžku \(|KM| = |KD| + |DM| = 5/2 + 3/2 = 4\). Dosadením do vzorca z úvodu riešenia tak dôjdeme k výsledku \[S_{KLM} = \frac{|KM| \cdot |LD|}{2}=\frac{4 \cdot \frac{\sqrt{15}}{2}}{2}=\sqrt{15}.\]
Odpoveď. Trojuholník \(KLM\) má obsah \(\sqrt{15}\) cm\(^2\).
Iné riešenie*. Keď narysujeme presne obe kružnice \(k_1\), \(k_2\) a zodpovedajúci bod \(M\), nadobudneme podozrenie, že \(|KM| = |AB|\) a bod \(L\) je taký bod Tálesovej kružnice \(k\) nad priemerom \(KM\) so stredom \(E\), ktorý leží na osi úsečky \(EB\) . Skutočne, pri
opísanej voľbe bodu \(M\) a konštrukcii bodu \(L\) bude platiť \(|BL| = |EL| = 2\) cm, takže aby sme sa presvedčili, že sa jedná naozaj o bod \(L\) zo zadania úlohy, stačí overiť, že aj \(|AL| = |AB| = 4\) cm. Keďže (písané bez jednotiek) \(|EM| = 2\), \(|BM| = |AK| = 1\), a teda \(|BD| = |ED| =\frac{1}{2}\) a \(|AD| =\frac{7}{2}\), podľa Pytagorovej vety použitej postupne na pravouhlé trojuholníky \(BDL\) a \(ADL\) pre takto zostrojený bod \(L\) máme
\[|DL|^2 = 2^2 - \bigg( \frac{1}{2}\bigg)^2=\frac{15}{4}, \ \ \ \ \ \ |AL|^2=\bigg(\frac{7}{2}\bigg)^2+ 2^2 - \bigg(\frac{1}{2}\bigg)^2= 4^2.\]
Tým je naša hypotéza overená. Obsah trojuholníka \(KLM\) už spočítame ľahko: \[S_KLM =\frac{1}{2}|KM| \cdot |LD| = 2|DL|\,\text{cm} =\sqrt{15}\,\text{cm}^2.\]
Výpočet dĺžky odvesny \(LM\) bez medzivýpočtu výšky \(LD\) je totiž prakticky nemožný.↩︎
Inou možnosťou pre výpočet výšky \(LD\) na rameno \(AB\) rovnoramenného trojuholníka \(ABL\) je vypočítať jeho výšku \(AS\) na základňu \(BL\) (použitím Pytagorovej vety pre trojuholník \(ABS\)) a potom porovnať dvojaké vyjadrenie obsahu trojuholníka \(ABL\) cez jeho výšky \(AS\) a \(LD\).↩︎
Úloha B-66-I-3-N1
Riešenie*
Úloha 66-I-5-N2
Riešenie*
Úloha 66-I-3-D2
Riešenie*
Úloha 64-S-1
Riešenie*
Pre \(x \geq 1\) vyjde rovnica \(x^2 = 1\); z jej dvoch riešení \(x = -1\) a \(x = 1\) predpokladu \(x \geq 1\) vyhovuje iba \(x = 1\).
Z danej sústavy potom jednoducho dopočítame hodnoty \(y = -1\) a \(z = 2\). Sústava má teda jediné riešenie \((x, y, z) = (1, -1, 2).\)
Úloha (Holton 2010), úloha 20, str. 110
Riešenie*
Komentár
Úloha má krátke a jednoduché zadanie, jej riešenie však vyžaduje uplatnenie znalostí o deliteľnosti aj zápis čísla v rozvinutom tvare.Holton, Derek Allan. 2010. A First Step to Mathematical Olympiad Problems. 1st edition. Danvers, USA: World Scientific.
Úloha 64-I-5-N1
Riešenie*
Úloha 62-II-1
Riešenie*
Úloha 60-I-4
a) Ukážte, že v prípade \(n = 7\) sa dajú žiaci požadovaným spôsobom vždy rozdeliť.
b) Zistite, či možno žiakov takto vždy rozdeliť aj v prípade \(n = 8\).
Riešenie*
Takže stačí rozdeliť žiakov tak, že každý v trojčlennej skupine má v nej kamaráta. Preto do nej dáme hociktorého zo žiakov a k nemu niektorých jeho dvoch kamarátov.
b) Vezmime hocijaké rozdelenie 8 žiakov na dve štvorčlenné skupiny. Ak toto rozdelenie nevyhovuje učiteľkinmu zámeru, máme nejakého žiaka \(X\), ktorý je zle zaradený – má všetkých svojich štyroch kamarátov \(A, B, C, D\) v druhej skupine. Ukážeme, že vieme vymeniť \(X\) a niektorého zo žiakov \(A, B, C, D\) tak, že počet zle zaradených žiakov sa zmenší.
Po každej zo štyroch výmen prichádzajúcich do úvahy \(X\) prestane byť zle zaradený a všetci traja žiaci, ktorí budú s \(X\) v skupine, budú dobre zaradení, lebo sú to kamaráti žiaka \(X\). Žiaci \(K, L, M\), ktorí boli pred výmenou v skupine s X, môžu byť po výmene zle zaradení len vtedy, ak boli zle zaradení aj predtým (lebo \(X\) nemal ani jedného z nich za kamaráta). Keďže žiak K má štyroch kamarátov a nekamaráti sa s \(X\), musí mať aspoň jedného kamaráta \(Y\) aj v skupine obsahujúcej žiakov \(A, B, C, D\), a keď žiaka \(Y\) vymeníme s \(X\), bude mať vo svojej novej skupine za kamaráta \(K\).
Ukázali sme teda, že výmenou žiakov \(X\) a \(Y\) počet zle zaradených žiakov klesol. Dostali sme nejaké nové rozdelenie; ak v ňom je aspoň jeden žiak zle zaradený, môžeme zopakovať predošlý postup a opäť znížiť počet zle zaradených žiakov. Po nanajvýš ôsmich krokoch dostaneme rozdelenie, v ktorom už nie sú žiadni zle zaradení žiaci.
Iné riešenie časti b). Uvažujme všetky možné rozdelenia žiakov na dve štvorčlenné skupiny. Rozdelenia, kde niekto nemá vo svojej skupine žiadneho kamaráta, budeme nazývať zlé, ostatné budú dobré. Koľko je zlých rozdelení? Ak má žiak \(X\) aspoň päť kamarátov, aspoň jeden z nich musí byť v jeho skupine. Ak má žiak \(X\) iba štyroch kamarátov, a všetci sú v druhej skupine, máme len jedno jediné rozdelenie s touto vlastnosťou. Celkovo teda k danému žiakovi \(X\) existuje nanajvýš jedno rozdelenie, ktoré je zlé. Za \(X\) môžeme zobrať jedného z 8 rôznych žiakov, preto zlých rozdelení je nanajvýš 8 (niektoré sme možno zarátali viackrát). Pritom všetkých rozdelení je \(\binom{7}{3}=35\), čiže aspoň 27 z nich je dobrých.